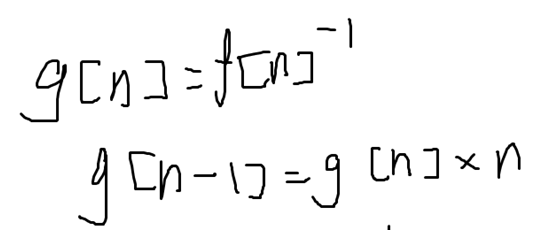数论:
1.高精除单精:
从最高位开始除,每次保留整除的结果,然后余数乘10传给下一位;

高精除高精:

重载:1.写在struct里面 2.不需动脑子的代码
最后一个for循环:处理前导0;
高精度开方:


神仙高精度开方:
两位分一组,然后每次先用目前求得的数*20;然后求一个最小的x,使得我们(目前求得的数*20+x)*x,然后使之小于且最接近于我们所落下的数位;
快速幂:
思路就是任何一个数都可以拆分几个2的乘方相乘?

表示a^b%k;
蒟阵:
矩阵加法:对应的每一格加起来;
矩阵乘法:n*m m*r=>n*r;
新矩阵ci,j=Σ(k=1~m)Ai,k*Bk,j;
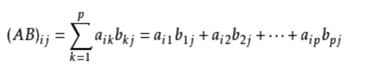

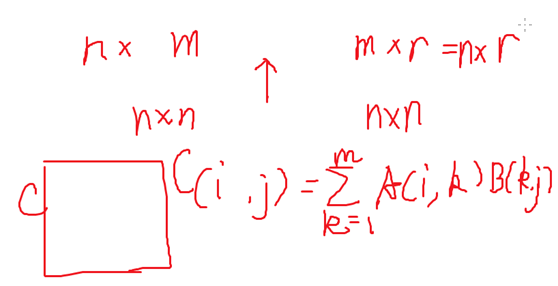
蒟阵快速幂:

![]()
转置矩阵↑↓
|3 ,1,0|
|-8,0,1|
|11,0,0|
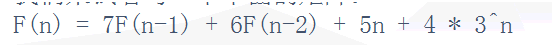
|f(n-1),f(n-2),n,3^n,1|* |7,1,0,0,0|
|6,0,0,0,0|
|5,0,1,0,0|
|4,0,0,3,0|
|0,0,1,0,1|
高斯消元:
1交换两行
2一行的倍数减去另一行;
消成上三角矩阵或上三角矩阵;
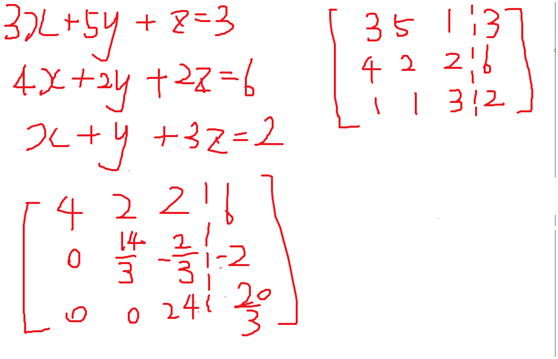
欧拉筛与积性函数:

然后欧拉筛:
e[i]表示这个数i的最小素因子;

基本思路还是埃氏筛,只不过做了改进;
对于质数来说,它的最小素因子显然就是他自己。然后我们枚举每一个数之后,枚举质数表,使当前质数都*我们当前枚举的数,这样实际上的效果是在满足条件的前提下,将某个质数的x倍都算出来筛掉(其中x>=某个质数),对于欧拉筛来说,我们要保证某个合数只被它的最小质因子筛。
对于一个合数,它的最小质因子就是最先乘到的质数,(啊有点乱,感性理解),然后当我们枚举到e[i]==prime[j]时:(e[i]>prime[i]时,就不是最小质因子筛)






求欧拉函数&莫比乌斯函数

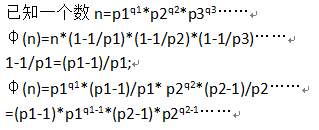

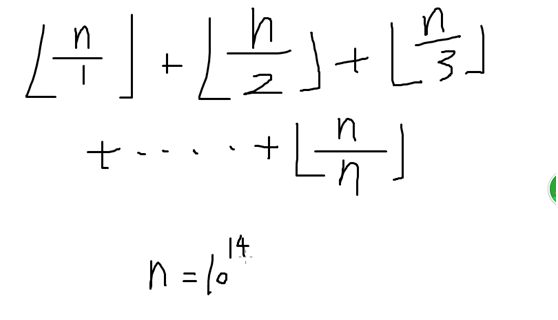

对于一个数i,我们令k=n/i;那么接下来会有不少数用n/某个数=k;这样我们求在哪结束n/某个数=k,可以用n/k,得到的结果就是最后一个n/某个数=k的位置;

神仙gcd:

贪心搜索:
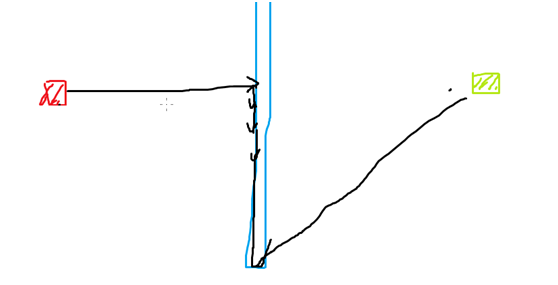
不知道贪心搜索给出的是否为最优解;
A*:
g:从起点出发走了多少步(广搜:走了多少出,深搜:到根节点的距离)
h:当前点到终点 理想的最优情况 需要走几步;(穿墙而过可海星?)
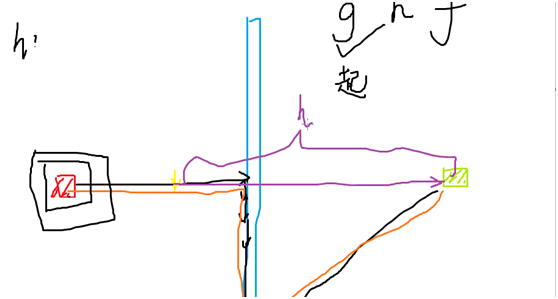
f:f=g+h;
A*是让节点按f排个序,然后哪个点比较小,就让哪个点先扩展;

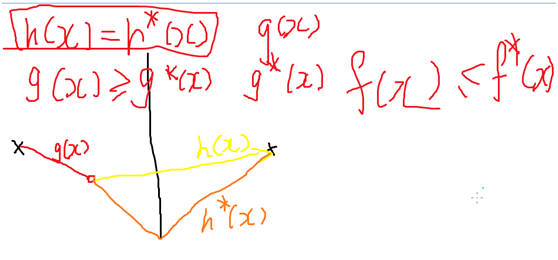
 在大部分A*搜索中g*(x)=g(x);
在大部分A*搜索中g*(x)=g(x);


A*第一次到终点时就是最优解;

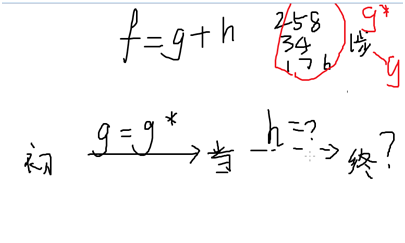
h:加曼哈顿距离:1~8 横着的差的绝对值+竖着的差的绝对值

一定会比bfs快;
判断是否搜到过,拍成一个长整型×

我觉得可以学 :
:
处理数组,算每个数字右边有多少个数字比它小

对于每一位,从右到左分别乘0!,1!,2!,3!,……;
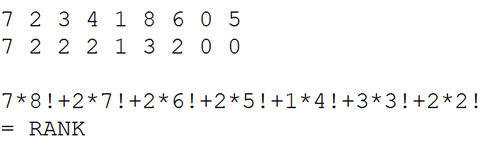
K短路:


g表示某个点从根节点下来走了几步
h当前节点到
判断g+h>D return;
Ans=7; g+h>7 return;
逆元:


因为ax≡1(mod p)
所以ax-1=bp;
那么:ax-bp=1;

上方:打个表;
下方: