日常不想放题目
(Solution):
题目中要求可以查询历史状态,最暴力的想法是开(a[m][n])的二维数组,每次修改暴力复制并修改,每次查询暴力扫描,时间复杂度是(O(m*n))的,但这显然是不行的.
这个时候其实很容易想到线段树,但线段树维护的是当前状态而无法维护历史状态,一种暴力的想法是开(m)棵线段树,但这样(MLE)的风险可谓巨大。
但我们发现,因为题目修改的是一个点的值,在线段树上,会被修改的点只有(log_n)个,因此可以每次只新建这(log_n)个结点
举个例子:
一个六个数据的线段树
初始数值: 0 4 0 7 0 3(发现没什么用
建成一棵线段树:
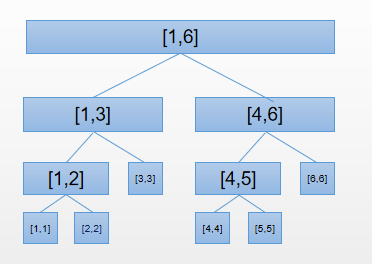
假设我们要修改第二个位置,那么被修改的也就是橙色部分:
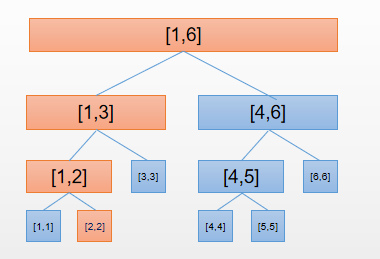
所以可以只新建这一部分节点:
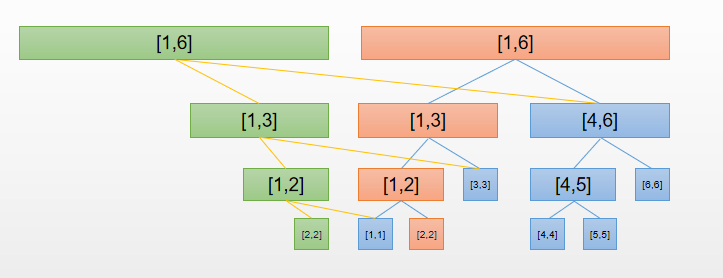
于是树就变成了这个亚子(
因为需要不断的新建节点,因此不能按照常规的(k<<1,k<<1|1)来记录线段树的儿子,而需要开专门的数组来记录左右儿子的编号;
我们只需要记录每次修改后的根节点(rt[i]),在查询第(v)次操作时顺着(rt[v])查找就好
具体实现不是很难(这是我第一次自己按思想自己写出来的数据结构
(Code):
#include<bits/stdc++.h>
using namespace std;
inline int read() {
int ans=0;
char last=' ',ch=getchar();
while(ch>'9'||ch<'0') last=ch,ch=getchar();
while(ch>='0'&&ch<='9') ans=(ans<<1)+(ans<<3)+ch-'0',ch=getchar();
if(last=='-') ans=-ans;
return ans;
}const int mxn=1000010;
int n,m,a[mxn];
int cntn,rt[mxn<<5];
struct node {
int l,r,val;
}t[mxn<<5];
int build(int l,int r) {
int now=++cntn;
if(l==r) {
t[now].val=a[l];
return now;
}
int mid=(l+r)>>1;
t[now].l=build(l,mid);
t[now].r=build(mid+1,r);
return now;
}
int modify(int k,int l,int r,int x,int p) {
int now=++cntn;
if(l==r) {
t[now].val=p;
return now;
}
int mid=(l+r)>>1;
if(x<=mid)
t[now].l=modify(t[k].l,l,mid,x,p),t[now].r=t[k].r;
else
t[now].r=modify(t[k].r,mid+1,r,x,p),t[now].l=t[k].l;
return now;
}
int query(int k,int l,int r,int x) {
if(l==r)
return t[k].val;
int mid=(l+r)>>1,rtn=0;
if(x<=mid)
rtn=query(t[k].l,l,mid,x);
else
rtn=query(t[k].r,mid+1,r,x);
return rtn;
}
int main() {
n=read();
m=read();
for(int i=1;i<=n;i++)
a[i]=read();
rt[0]=build(1,n);
for(int i=1,v,opt,x,y;i<=m;i++) {
v=read();
opt=read();
if(opt==1) {
x=read();
y=read();
rt[i]=modify(rt[v],1,n,x,y);
}
if(opt==2) {
x=read();
printf("%d
",query(rt[v],1,n,x));
rt[i]=rt[v];
}
}
return 0;
}