https://www.cnblogs.com/frankchenfu/p/7107019.html
最长上2升子序列(LIS)。
【题目描述】
给定N个数,求这N个数的最长上升子序列的长度。
【样例输入】
7
2 5 3 4 1 7 6
【样例输出】
4
什么是最长上升子序列? 就是给你一个序列,请你在其中求出一段不断严格上升的部分,它不一定要连续。
就像这样:2,3,4,7和2,3,4,6就是序列2 5 3 4 1 7 6的两种选取方案。最长的长度是4.

那么,怎么求出它的最大上升子序列长度为4呢?这里介绍两种方法,都是以动态规划为基础的。
首先,我们先介绍较慢(O(n2n2))的方法。我们记num为到这个数为止,最长上升子序列的长度。
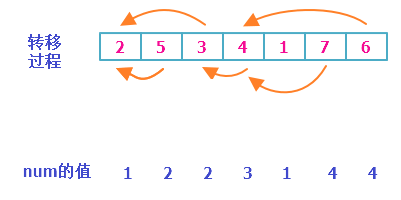
这种方法就是每一次寻找“可以接下去的”,换句话说,设原序列为a,则
当aj<ai(j<i)aj<ai(j<i)且numj+1>numinumj+1>numi时,numi=numj+1numi=numj+1。
对于每一个数,他都是在“可以接下去”的中,从前面的最优值+1转移而来。
因此,这个算法是可以求出正确答案的。复杂度很明显,外层i枚举每个数,内层j枚举目前i的最优值,即O(n2n2)。
那么,有没有更快的方法呢?当然有。这回要用到二分。
我们回想一下,在上面O(n2n2)的程序中,哪些地方看起来比较费时?
没错,就是内层用于更新i的循环。因为每一次他都要查找一遍,效率并不高。
回到题目,我们发现,他只要我们求长度,所以?
我们可以模拟一个栈。
所以每遇到一个比栈顶元素大的数,就放进栈里,遇到比栈顶元素小的就二分查找前边的元素,找到一个“最应该被换掉的元素”,用新数去更新前边的元素。
这个算法不难证明也是正确的。因为前面每一次的枚举都换成了二分,内层的复杂度从nn降到了log2log2,外层不变。所以总的复杂度是O(nlog2nnlog2n)。
注意: 两种方法都是用来找到 最大长度的,第一个方法改编下可以记录下一种满足要求的序列,而第二种方法只能得出正确的长度,里面存放的数据,不能保证是合法的序列。 第一种方法:
import java.util.Scanner;
class Main1{
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
int n = cin.nextInt();
int[] a = new int[n];
for(int i = 0; i < n; i++) {
a[i] = cin.nextInt();
}
int num[] = new int[n];
int pre[] = new int[n];
for(int i = 0; i < n; i++) {
num[i] = 1;
for(int j = 0; j < i; j++) {
if(a[i] > a[j] && num[j] + 1 > num[i]) {
num[i] = num[j] + 1;
pre[i] = j; //记录它的前一个点
}
}
}
int max = -0x3f3f3f3f;
int x = 0;
for(int i = 0; i < n; i++) {
if(max < num[i]) { //只找到第一个最大的
max = num[i];
x = i;
}
}
System.out.println(max);
for(int i = 0; i < max; i++) {
System.out.print(a[x] + " ");
x = pre[x];
}
}
}
/*
7
2 5 3 4 1 7 6
*/
第二种方法:
import java.util.Scanner;
class Main2{
public static void main(String[] args) {
Scanner cin = new Scanner(System.in);
int n = cin.nextInt();
int[] a = new int[n];
for(int i = 0; i < n; i++) {
a[i] = cin.nextInt();
}
int cnt = 0;
int num[] = new int[n];
num[0] = a[0];
for(int i = 1; i < n; i++) {
if(a[i] < num[cnt]) {
int x = erfen(num, 0, cnt, a[i]);
System.out.println("find: w " + num[x] + ", a[i] " + a[i]);
num[x] = a[i];
}
else {
num[++cnt] = a[i];
}
}
System.out.println("最长上升子序列长度为:" + (cnt + 1));
// 以下为一种:注意这个不一定是合法的序列,但是保证长度一定正确:
for(int i = 0; i <= cnt; i++) {
System.out.print(num[i] + " ");
}
}
public static int erfen(int num[], int left, int right, int key) {
if(left < right && num[left] > key) {
return 0;
}
int mid;
while(left < right) { // 去掉等号就是返回最小大于key的元素下标,最大小于的则是它加一
mid = left + (right - left) / 2;
if(key == num[mid]) {
return mid;
}
else if(key < num[mid]) {
right = mid - 1;
}
else {
left = mid + 1;
}
}
return left;
}
}
/*
7
2 5 3 4 1 7 6
*/