在一个排列中,如果一对数的前后位置与大小顺序相反,即前面的数大于后面的数,那么它们就称为一个逆序。一个排列中逆序的总数就称为这个排列的逆序数。
eg:
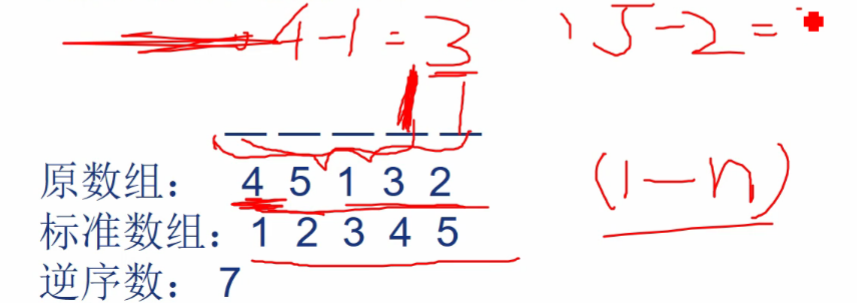
原序列: 4 5 1 3 2
标准序列:1 2 3 4 5
逆序数 :7
可以用树状数组做:讲解:00:58 : 00 https://www.nowcoder.com/study/live/153/11/1
对于标准的1到n的数字:
#include <iostream>
#include <cstring>
#include <cstdio>
using namespace std;
int sum[50005]; //sum[x]表示的是区间为2^k个元素的和,k为x的二进制末尾0的个数,以为最后一个元素为a[x],
int n; //所以sum[x] = a[n - 2^k + 1] + ...+ a[x]; 看图理解
void update(int pos, int val){
while(pos <= n){ //一直更新到最后
sum[pos] += val;
pos += (pos & (-pos)); //pos && (-pos)找到pos二进制末尾一个1
}
}
int query(int pos){
int ans = 0;
while(pos > 0){ //一直加到0
ans += sum[pos];
pos -= (pos & (-pos));
}
return ans;
}
int main(){
int ans = 0, x;
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", &x);
update(x, 1);
for(int i = 1; i <= n; i++){
cout << sum[i] << " ";
}
cout << endl;
int temp = query(x);
ans += x - temp;
cout << temp << "tem" <<endl;
}
printf("%d
", ans);
return 0;
}
#include <iostream>
#include <algorithm>
#include <cstring>
#include <cstdio>
using namespace std;
int sum[50005]; //sum[x]表示的是区间为2^k个元素的和,k为x的二进制末尾0的个数,以为最后一个元素为a[x],
int n; //所以sum[x] = a[n - 2^k + 1] + ...+ a[x]; 看图理解
struct node{
int pos, x; //pos:记录输入的位置,x:值
}a[100005];
int b[100005];
bool cmp(node x, node y){
return x.x < y.x;
}
void update(int pos, int val){
while(pos <= n){ //一直更新到最后
sum[pos] += val;
pos += (pos & (-pos)); //pos && (-pos)找到pos二进制末尾一个1
}
}
int query(int pos){
int ans = 0;
while(pos > 0){ //一直加到0
ans += sum[pos];
pos -= (pos & (-pos));
}
return ans;
}
int main(){
long long ans = 0, x; //int错了
scanf("%d", &n);
for(int i = 1; i <= n; i++){
scanf("%d", &a[i].x);
a[i].pos = i;
}
sort(a + 1, a + n + 1, cmp);
for(int i = 1; i <= n; i++){
b[a[i].pos] = i;
}
for(int i = 1; i <= n; i++){
x = b[i];
update(x, 1);
int temp = query(x);
ans += x - temp;
}
printf("%d
", ans);
return 0;
}