最近看到了这么一道题,觉得很有意思,所以就来给大家分享一下:
对于下面这个图形: 每个正方形的边长为1, 那么从A到Z的最短路径条数有多少?

这道题的解法有下面的两种。
第一种(规律):
首先,我们可以肯定的是:最短路径为6.
考虑将这个矩形补全,那么从A到Z,需要做的就是从左往右走四步,从上往下走两步。这个是刚好可以满足条件的。 我们只需要从这6步中选出两步是朝下的即可,那么剩下的4步朝右的也就随之确定了。 所以,C(2, 6),但是这里并不是完整的,而缺少的那两个朝下的,可以发现, 刚好每个对应着一个路径,所以最终就是 C(2, 6) - 2。
第二种(动态规划):
我这里粗略的画了一下:
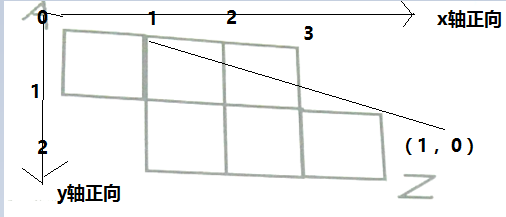
即根据图形特点建立坐标轴,我们设 d[x, y] 为从A点出发到(x, y)左边处时,最短需要走的步数。
显然,到(1, 0)为1, 到(2, 0)为2, 到(3, 0)为3。 到(0, 1)为1, 到(1, 1)为2,即我们可以先向右走,然后再向下走;也可以先向下走,然后再向右走,就是这两种,如下:

其实,我们根据规律就可以得到下面的状态转移方程:
d[x, y] = d[x - 1, y] + d[x, y - 1];
这里其实也是很好理解的,到d[x, y]就是到达x,y 这个点的最短路径的条数。
到这一步有两种方法,一种是最后一步在 (x - 1, y) 这点,另一种就是到达 (x, y - 1)这一点, 所以到达(x, y)这点一共就这两种可能,相加即可 ,即 d[x - 1, y] + d[x, y - 1]。