摘自百度百科:
差分(difference)又名差分函数或差分运算,差分的结果反映了离散量之间的一种变化,是研究离散数学的一种工具。它将原函数 f(x) 映射到 f(x+a) - f(x+b) 。差分运算,相应于微分运算,是微积分中重要的一个概念。总而言之,差分对应离散,微分对应连续。差分又分为前向差分、向后差分及中心差分三种。
看不懂?没关系,让我们用实例了解差分算法的思想
差分数组
栗子:现有一无限长的直线,每次操作给出 ([L,R]) 对某线段进行覆盖,在 (M) 次操作后求任意整数点被覆盖的次数
由于求的是整数点被覆盖的次数,所以显然这是一个离散数学的模型
所以一个直观的做法是用一个数组 (cnt) 记录每个点被覆盖的次数,每次遍历 ([L,R]) 中所有的整数点进行累加,最后 (O(1)) 查询任意点
for (int i=l;i<=r;i++) cnt[i]++;
时间复杂度为 (O(M*len))
这个复杂度一般来说不够优秀,那么我们如何利用条件的特殊性质进行优化呢?
注意到给出的线段上所有点都是连续的,或许只关心首尾坐标加上前缀和的操作就可以实现统计
引入神奇差分数组 (c[]),它记录的是整个序列的差分情况,而不关心具体的次数数值
具体操作:在读入每一个 ([L,R]) 时,将 (c[L]++,c[R+1]--;)
所有操作结束后对 (c[]) 取前缀和 (sum[]),得到的 (sum[i]) 便是坐标为 (i) 的点的被覆盖次数

代码如下:
// 直线范围 [1,n]
for (int i=1;i<=m;i++) {
scanf("%d%d",&l,&r);
c[l]++,c[r+1]--;
}
for (int i=1;i<=n;i++) sum[i]=sum[i-1]+c[i];
例题:Luogu: 数据结构
树上差分
树的介于图和数组之间的数据结构,它如下基本性质:
((1)) 任意两个节点之间有且只有一条路径
((2)) 根节点确定时,一个节点只有一个父亲节点
这两个性质都是很优秀的,我们可以把差分算法的思想在树上套用,具体实例如下
边差分
栗子:现有一棵树,每次给出 (x,y) 两点,将两点路径上经过的所有边加权,最后求每条边的权值
树上差分问题都可以用树链剖分轻易解决,但本文只介绍相对简单的差分做法
我们知道树上两点路径是:(x o LCA(x,y) o y),其中 (LCA) 为两点的最近公共祖先
由于 (LCA) 往上的节点、(x,y) 往下的节点都与该路径无关,所以我们关心的差分边界即为这三枚点
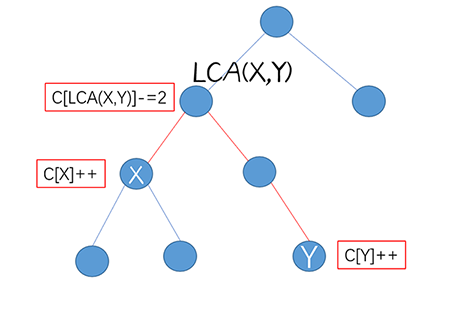
操作公式:(c[LCA(x,y)]--,c[x]++,c[y]--;)
这个公式直观上不难理解,但按理说遍历的顺序是从根到叶,那为什么是上减下加呢?
这是因为树上的差分为了不影响其他子分支的结果,统计是在回溯时完成的,可以自行想象一下相反的过程
(dfs) 遍历统计时累加某节点的差分值和连向该节点子节点的边的统计值即为该节点连向父节点的边的统计值
代码如下:
// c[x]++,c[y]++,c[LCA(x,y)]-=2;
struct Edge { int t,id; }; // t为边的指向,id为边的编号
vector<Edge> G[MAXN];
int diff(int u) {
int sum=c[u]; //初始值为节点u的差分值
for (int i=0;i<(int)G[u].size();i++) {
if (vis[G[u][i].t]) continue;
vis[G[u][i].t]=true;
ans[G[u][i].id]=diff(G[u][i].t);
sum+=ans[G[u][i].id]; //累加每条由u连向子节点的值
}
return sum; //统计出节点u->u父亲这条边的权值
}
例题:Codeforces: Fools and Roads
点差分
栗子:现有一棵树,每次给出 (x,y) 两点,将两点路径上经过的所有点加权,最后求每个点的权值
现在我们统计的对象由边变成了点,丧失了边一定是在两点之间的这一性质,稍加转换即可
显然统计边的公式不能继续使用( 比如汇点 (LCA) 就不会给加到),需要转换成以下公式:
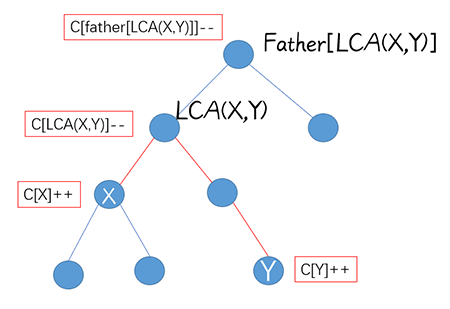
(c[LCA(x,y)]--,c[father[LCA(x,y)]]--,c[x]++,c[y]++;)
可以自行脑部以下统计的过程,会发现在 (LCA) 先减掉一次之后统计值刚刚好(抵消了一个子节点加的)
代码如下:
// c[x]++,c[y]++,c[LCA(x,y)]--,c[father[LCA(x,y)]]--;
vector<int> G[MAXN];
int diff(int u) {
int sum=c[u]; //初始值为节点u的差分值
for (int i=0;i<(int)G[u].size();i++) {
if (vis[G[u][i]]) continue;
vis[G[u][i]]=true;
ans[G[u][i]]=diff(G[u][i]);
sum+=ans[G[u][i]]; //累加节点u子节点的被覆盖次数
}
return sum; //统计出节点u的被覆盖次数
}