第十三届全国大学生信息安全竞赛-创新实践能力赛 Build 环节
赛题设计说明
题目信息:
-
题目名称: carpet(地毯)
-
预估难度: 中等偏易
题目描述:
本题属于 Reverse 类型,核心考点是算法设计能力。
程序在给 64x64 出平面中不能覆盖的方格之后,做题者需要构造
1365 块 L 形地毯的放置形态和位置,以保证除了给定方格其余方格
都被完美覆盖,可以通过数学证明双向解法唯一。
如果把给定方格视为完整消息串,构造出的放置方法为摘要信息,
那么 exp 可以视为一个注册机,根据给出的不同坐标进行 Hash。
题目考点(至少2点)
-
Linux 平台 ELF 文件的逆向分析
-
信息搜集与二进制工具的使用
-
分治算法设计与实现能力
思路简述
-
在相应 Linux 环境下运行本地或者远程程序,得到预定的 hint
-
将二进制 ELF 文件拉近相应工具进行反汇编,查壳、保护机制等
-
设计利用的算法(分治),并使用编程实现
-
在 pwntools 等模块下完成 OI 交互,成功 getshell
题目提示(至少3点)
- 运行程序后提示平面地图的大小
- 运行程序后提示地毯形状对应的编号
- 利用成功/失败后程序会进行相应反馈
- 内嵌后门函数 getshell()
其他补充
- 编译环境:
System: Ubuntu 16.04.6 LTS
gcc: 5.4.0 20160609
glibc: ldd (Ubuntu GLIBC 2.23-0ubuntu11) 2.23 - 测试环境:
System: Ubuntu 16.04.6 LTS
gcc: 5.4.0 20160609
glibc: ldd (Ubuntu GLIBC 2.23-0ubuntu11) 2.23
Writeup
拿到 ELF 文件和远程地址,首先查看一下保护
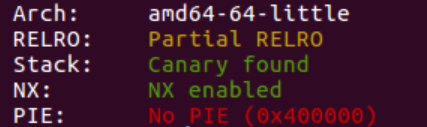
在相应环境运行一下,得到一个很重要的 hint
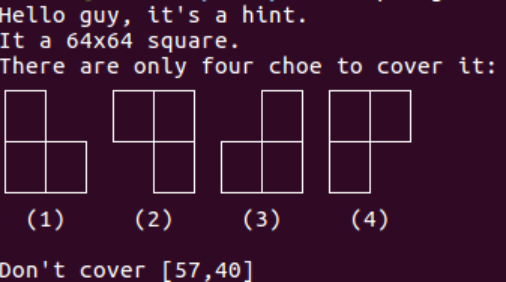
初步理解就是需要在 64x64 的正方形中用 L 形地毯覆盖完全,而单独给定的一个坐标不能被覆盖
1)64x64 = 4096,4096 / 3 = 1365 ······ 1
2)可以用数学归纳法证明边长为 2^n 的正方形可以被该方式完美覆盖
简单推导之后发现本题的解是一定存在的
为了印证游戏规则,还需要把该文件拉入反汇编软件进行更加详细的分析

map 看起来就是保存地图的函数
[v10,v11] 是用随机数生成的坐标

随后读入了 1365 组数,每组由三个整数 v5,v6,v7 组成,传入 cover() 当参数
定位到 cover() 函数查看:

发现有很多左移 6 位的操作,2^6 = 64,和此前提示的 64x64 形状相同
判断出 map 是一个二维数组,a1 和 a2 是 map 的两个下标,a3 是此前绘出的地毯形状
那么这个函数的功能就是在 [a1,a2] 为中心的位置 “铺上” 相应形状的地毯
回到 main() 函数:
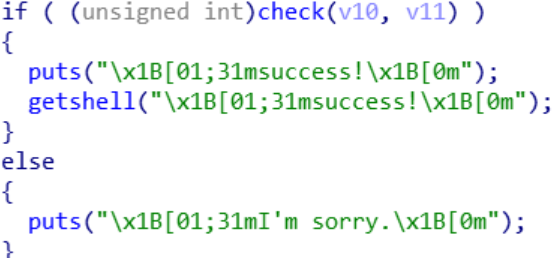
在全部读入结束之后调用了 check(v10,v11),其中 [v10,v11] 是之前给的不能被覆盖的坐标
看函数名就知道这大概是一个验证覆盖是否完美的程序
check() 函数:
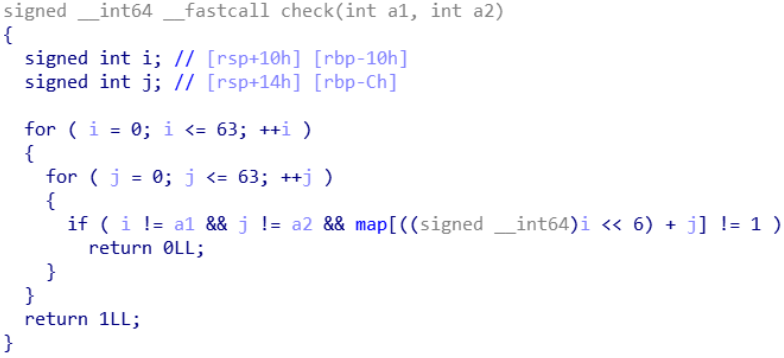
果然是在 [0,64) 的横纵范围遍历 map,遍历到 [a1,a2] 的情况单独处理
验证是否除了 [a1,a2] 以外的所有方格都被完美覆盖一次
如果验证成功,则返回 True,随后 main() 函数会调用 get_shell()
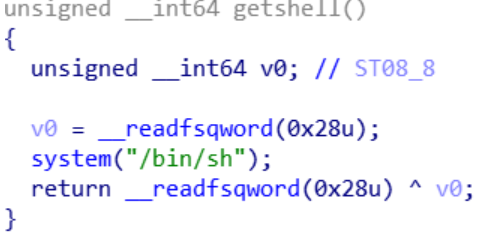
分析到这里我们的任务目标就很清晰了,就是要构造合法的输入铺设地毯,
这里利用了 pwntools 模块进行 OI 操作
开始设计算法:
这个问题,似乎无从下手,于是我们可以先考虑最简单的情况,既正方形是 2x2 时
这时,无论不能覆盖四个格子中的哪个,我们都可以用一块毯子填满
继续考虑 4x4 的情况
我们已经知道了解决 2x2 的格子中有一个障碍的情况如何解决,因此我们可以尝试构造这种情况
首先,显然可以将 4x4 的盘面划分成 4 个2*2的小盘面,其中一块已经存在一个障碍了
而我们只需在正中间的 2*2 方格中放入一块地毯,就可以使所有小盘面都有一个障碍
于是,4x4 的情况就解决了

我们可以推广到一般情况,即当 (2k)x(2k) 时(在这道题中 k = 6 ),
我们均可以将问题划分为 4 个 (2(k-1))x(2(k-1)) 的子问题,然后分治算法递归解决
于是编写 exp:
from pwn import *
import re
cnt=0
def prt(px, py, t):
global cnt
io.send(str(px)+' '+str(py)+' '+str(t)+'
')
io.recv(timeout=0.01)
cnt = cnt + 1
print cnt
def fun(siz, x, y, tx, ty):
if (siz==1):
if (tx==x and ty==y+1):
prt(x+1, y, 1)
elif (tx==x+1 and ty==y):
prt(x, y+1, 2)
elif (tx==x and ty==y):
prt(x+1, y+1, 3)
elif (tx==x+1 and ty==y+1):
prt(x, y, 4)
else:
prt(x, y, 5)
else:
tmp = ((1<<siz)+1)>>1
if (tx<x+tmp and ty<y+tmp):
fun(siz-1, x, y, tx, ty)
fun(siz-1, x, y+tmp, x+tmp-1, y+tmp)
fun(siz-1, x+tmp, y, x+tmp, y+tmp-1)
fun(siz-1, x+tmp, y+tmp, x+tmp, y+tmp)
prt(x+tmp, y+tmp, 3)
elif (tx<x+tmp and ty>=y+tmp):
fun(siz-1, x, y, x+tmp-1, y+tmp-1)
fun(siz-1, x, y+tmp, tx, ty)
fun(siz-1, x+tmp, y, x+tmp, y+tmp-1)
fun(siz-1, x+tmp, y+tmp, x+tmp, y+tmp)
prt(x+tmp, y+tmp-1, 1)
elif (tx>=x+tmp and ty<y+tmp):
fun(siz-1, x, y, x+tmp-1, y+tmp-1)
fun(siz-1, x, y+tmp, x+tmp-1, y+tmp)
fun(siz-1, x+tmp, y, tx, ty)
fun(siz-1, x+tmp, y+tmp, x+tmp, y+tmp)
prt(x+tmp-1, y+tmp, 2)
else:
fun(siz-1, x, y, x+tmp-1, y+tmp-1)
fun(siz-1, x, y+tmp, x+tmp-1, y+tmp)
fun(siz-1, x+tmp, y, x+tmp, y+tmp-1)
fun(siz-1, x+tmp, y+tmp, tx, ty)
prt(x+tmp-1, y+tmp-1 ,4)
context.log_level = 'debug'
io = process('./target')
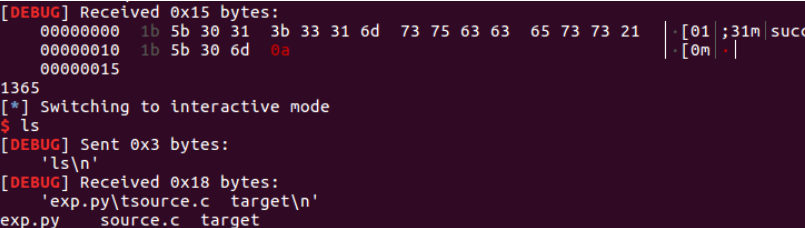
io.recvuntil("Don't cover [")
message = io.recvuntil(']
')
num = re.findall(r'd+',message)
fun(6, 0, 0, int(num[0]), int(num[1]))
io.recv(timeout=0.01)
io.interactive()
成功 getshell(),本题完成