1 . Arima时序分析模型
1.1 基础知识:
https://blog.csdn.net/huangtiao2509/article/details/78251101
1.2 Arima模型原理:
ARIMA模型是时间序列分析中应用最广泛的模型之一,ARIMA(p,d,q)由三个部分组成
- AR(p):AR是autoregressive的缩写,表示自回归模型。含义是当前时间点的值等于过去若干个时间点的回归——因为不依赖与别的解释变量,只依赖于自己过去的历史值,故称为自回归;如果依赖过去最近的p个历史值,称阶数为p,记为AR(p)模型。

- I(d):I是integrated的缩写,含义是模型对时间序列进行差分。因为时间序列分析要求平稳性,不平稳的序列需要通过一定手段转化为平稳序列,一般采用的方法就是差分,d表示差分的阶数。
如果d=0: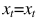
如果d=1: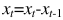
如果d=2: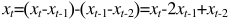
以此类推。
- MA(q):移动平均模型,和上面的移动平均法不同,这里本质上还是回归,含义是当前时间点的值等于过去若干个时间点的预测误差的回归;预测误差=模型预测值-真实值;如果序列依赖过去最近的q个历史预测误差值,称阶数为q,即为MA(q)模型。

1.3 模型衡量标准:
AIC和BIC,以及Inlkhd都是越接近0表示模型越好
https://zhuanlan.zhihu.com/p/22248464
2. 指数平滑法Holt-winters
总的来说,holt-winters将时间序列信号拆解为三个分量:
(1)平稳随机信号分量:
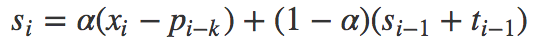
(2)趋势信号分量:
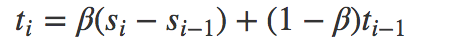
(3)周期性信号分量:
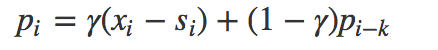
有三个参数:
其中 α是数据平滑因子, 0 < α < 1;β是趋势平滑因子,0 < β < 1; γ是季节改变平滑因子0 < γ < 1
对于三次指数平滑法,我们必须初始化一个完整的”季节“的值。至于如何选择参数αα,ββ,γγ,一个比较笨拙但可行的方法是反复试验,定义一个误差,比如平均绝对误差(Mean Absolute Error,MAE)或平均平方误差(Mean Squared Error,MSE),设定几个参数的范围,然后找到范围内误差最小的那组参数值。
具体代码实现:
https://blog.csdn.net/u010665216/article/details/78051192?locationNum=11&fps=1
小结:
ARIMA和Holter-winters是从不同的角度去分解时间序列信号的算法,两种方法各有它考虑信号的角度:holt-winters更多考虑的是如何做“平滑”;ARIMA则主要是基于“回归”的思想;在实际的时间序列分析问题中,面对更复杂的场景时,可能需要加入考虑其他的特征或者加入非线性,都可以从这些经典算法得到启发来不断改进和优化。
例如使用ensemble的思想将不同的算法得到的结果作为特征(或者说是“成分”)输入到新的模型中,又或者将某个算法中的平滑部分使用其他更巧妙的平滑方式取代,还可以借助神经网络来生成非线性特征,使得模型可以学习到非线性;另外,所有的回归算法也都可以用来解决预测问题。
回归预测模型的评估方法见先前的博客:https://www.cnblogs.com/zichun-zeng/p/8097455.html
时间信号常考虑的组成成分:(1)趋势;(2)季节性(或其他周期性);(3)噪音;(4)历史状态转换;(5)本身的时间序列特征;(6)其他。
此外,也有根据业务场景自身特点来分解信号的,比如按不同地区来分解,或者按不同间隔粒度来分解等。
其他应用实例:
https://www.jianshu.com/p/aaf8a3565a69