【算法日记】贝尔曼-福德算法

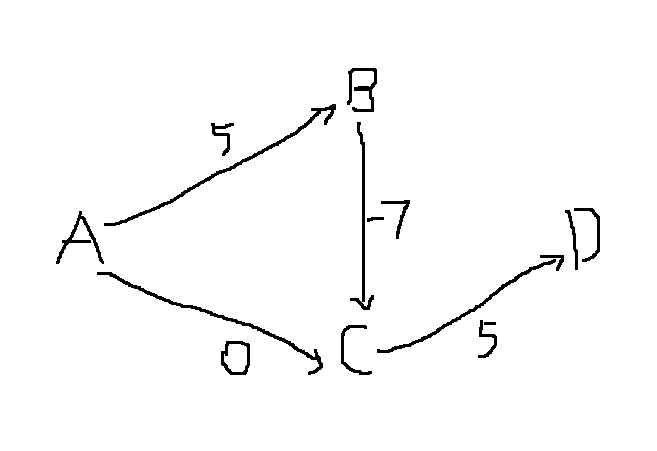
如上图使用Dijkstra算法将无法获取到最短路径

1.A->C->D   5

2.A->B...没有

最近路径为5.但是实际上B->C的路径为-2. A->B->C->D的最短开销为3

Dijkstra算法无法判断含负权边的图的最短路。如果遇到负权，在没有负权回路存在时（负权回路的含义是，回路的权值和为负。）即便有负权的边，也可以采用贝尔曼-福德算法算法正确求出最短路径。

算法实现

def bellman_ford( graph, source ):  
      
    distance = {}  
    parent = {}  
      
    for node in graph:  
        distance[node] = float( 'Inf' )  
        parent[node] = None  
    distance[source] = 0  
  
    for i in range( len( graph ) - 1 ):  
        for from_node in graph:  
            for to_node in graph[from_node]:  
                if distance[to_node] > graph[from_node][to_node] + distance[from_node]:  
                    distance[to_node] = graph[from_node][to_node] + distance[from_node]  
                    parent[to_node] = from_node  
  
    for from_node in graph:  
        for to_node in graph[from_node]:  
            if distance[to_node] > distance[from_node] + graph[from_node][to_node]:  
                return None, None  
  
    return distance, parent  
  
def test():  
    graph = {  
        'a': {'b': -1, 'c':  4},  
        'b': {'c':  3, 'd':  2, 'e':  2},  
        'c': {},  
        'd': {'b':  1, 'c':  5},  
        'e': {'d': -3}  
    }  
    distance, parent = bellman_ford( graph, 'a' )  
    print distance  
    print parent  
  
if __name__ == '__main__':  
    test()