要求:
1、输入一个整形数组,数组里有正数也有负数。
2、数组中连续的一个或多个整数组成一个子数组,每个子数组都有一个和。
3、如果数组A[0]......A[j-1]首位相邻,允许A[i-1],......A[n-1],A[0]......A[j-1]之和最大。
4、同时返回最大子数组的位置。
5、求所有子数组的和的最大值。
思路:
输入一个数组后,求其最大子数组。再将第一个数放在最后,从第二个数开始遍历求最大子数组,以此类推,直到最后一个数成为首元素。
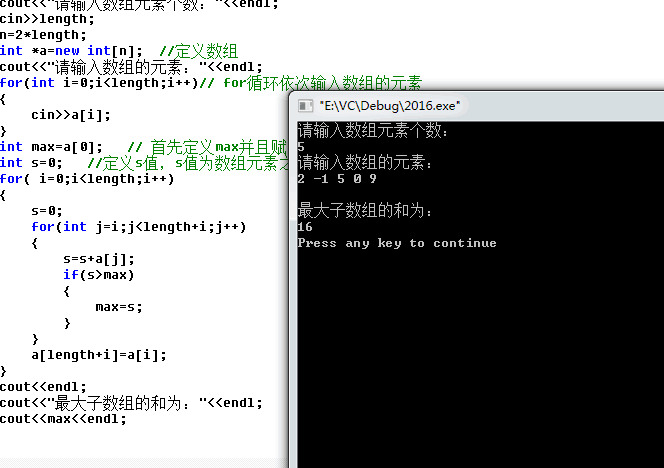
源代码:
#include<iostream>
using namespace std;
void main()
{
int length; //数组的个数
int n; //数组变化后的长度
cout<<"请输入数组元素个数:"<<endl;
cin>>length;
n=2*length;
int *a=new int[n]; //定义数组
cout<<"请输入数组的元素:"<<endl;
for(int i=0;i<length;i++)// for循环依次输入数组的元素
{
cin>>a[i];
}
int max=a[0]; // 首先定义max并且赋予第一个数组中的元素值
int s=0; //定义s值,s值为数组元素之和并且与max值比较
for( i=0;i<length;i++)
{
s=0;
for(int j=i;j<length+i;j++)
{
s=s+a[j];
if(s>max)
{
max=s;
}
}
a[length+i]=a[i];
}
cout<<endl;
cout<<"最大子数组的和为:"<<endl;
cout<<max<<endl;
}