●2017.3.31
●学习内容:网络流之求解最大流算法
引:最大流问题(maximum flow problem),一种组合最优化问题,就是要讨论如何充分利用装置的能力,使得运输的流量最大,以取得最好的效果。
●算法(e,我学了的……)
-
枚举算法:
-
由最小切割=最大流定理而来的暴力求法:
-
枚举所有割来求最小割:
-
代码图:
-
(资料上的东西,提供一种思路,正确性未知。)
-
增广路算法:
-
深度优先搜索(最大流 Ford-Fulkerson方法DFS实现):
-
不断从源点开始深搜增广路,直到没有了增广路为止。
-
特点:一旦搜索到一条增广路(能到达汇点且该路径的流量大于一)就回溯。
-
代码:
-
int dfs(int x,int low) { if(x==m) return low; if(vis[x]) return 0; vis[x]=1; for(int flow,i=1;i<=m;i++) { if(tub[x][i]&&(flow=dfs(i,min(low,tub[x][i])))) { tub[x][i]-=flow; tub[i][x]+=flow; return flow; } } return 0; } int maxflow(int s,int t) { int ans=0,flow; while(flow=dfs(1,INF)){memset(vis,0,sizeof(vis));;ans+=flow;} return ans; }
- 注意到每一大次dfs中(即从maxflow()调用),对于点x来说,i都是从1开始枚举,浪费了不少时间。我们便可以用一个cur[ ]数组来优化一下:
int dfs(int x,int low) { if(x==m) return low; if(vis[x]) return 0; vis[x]=1; for(int flow,i=cur[x];i<=m;i
++)//枚举时从cur[x]或cur[x]+1开始似乎都可以,因为疯狂的while()会直到没有增广路才停下来; { if(tub[x][i]&&(flow=dfs(i,min(low,tub[x][i])))) { cur[x]=i; tub[x][i]-=flow; tub[i][x]+=flow; return flow; } } return 0; } int maxflow(int s,int t) { int ans=0,flow; while(flow=dfs(1,INF)) {memset(vis,0,sizeof(vis));memset(cur,0,sizeof(cur));ans+=flow;} return ans; }
- 图示cur[ ]作用:
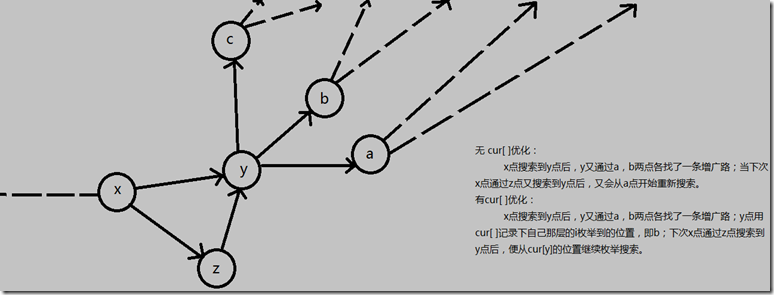
- Dinic算法
- 利用层次图进行的求最大流算法。
- 先进行bfs搜索建立层次图(计算每个点的深度),再dfs找增广路(每个点只能由深度比其小1的点搜索而来;把每个点在当层次图下的所有的增广路找完)
- 也可用cur[ ]优化
- 代码(Dinic+邻接链表)
bool bfs() { memset(vis,0,sizeof(vis)); queue<int>q; q.push(1); d[1]=1; vis[1]=1; while(!q.empty()) { int u=q.front();q.pop(); for(int i=head[u];~i;i=e[i].next)if(e[i].capo) { int v=e[i].to; if(vis[v]) continue; d[v]=d[u]+1; vis[v]=1; q.push(v); } } return vis[m]; } int dfs(int u,int res) { if(u==m||!res) return res; int flowout=0,v,f; for(int &i=cur[u];~i;i=e[i].next) { v=e[i].to; if(d[v]!=d[u]+1) continue; f=dfs(v,min(e[i].capo,res)); e[i].capo-=f; e[i^1].capo+=f; flowout+=f; res-=f; if(!res) break; } return flowout; } int maxflow() { while(bfs()) { for(int i=1;i<=m;i++) cur[i]=head[i]; ans+=dfs(1,INF); } }
- 注意上面两种算法的dfs的不同(前者是找到一条就猥琐的return了,后者是把该层次图下该点所有的增广路找完后,再return)
