●线段树的三个题（poj 3225，hdu 1542，hdu 1828）

●poj 3225 Help with Intervals(线段树区间问题)

○赘述题目

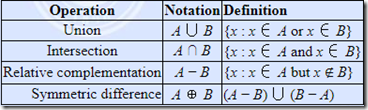
给出以下集合操作：

然后有初始的一个空集S，和以下题目给出的操作指令，并输入指令：

要求进行指令操作后，按格式输出集合S；

○题解

（此文标题就告诉了我们要用线段树维护。。。）

关键难点：

1.此题操作较复杂，如何较简便的进行线段树维护？

看看这位大师的转化：

。。。把各种操作转化为较为一致的区间修改后，线段树就能“开始表演”了。

2.涉及到开闭区间，又如何搞？

xio习的大师的方法：

比如输入的左右端点a,b

若是[ ]，则对应线段树的范围是 2a—2b

若是( ]，则对应线段树的范围是 2a+1—2b

若是[ )，则对应线段树的范围是 2a—2b-1

若是( )，则对应线段树的范围是 2a+1—2b-1

仔细去想想其中的妙处吧。

○值得注意的几点

1.注意覆盖操作和异或操作的关系：若有覆盖，则原来的异或标记失效；

2.在把输入指令转化为线段树的区间操作时，要让各种操作有尽可能多的一致性，

就如上面贴图中的方法，使得各种操作只用覆盖和异或这两个操作就能实现，这样可以在很大程度上降低代码复杂度和查错时间。

○代码

#include<cstdio>
#include<cstring>
#include<iostream>
#include <algorithm>
#define MAXN 131072
#define lson u<<1,l,mid
#define rson u<<1|1,mid+1,r 
using namespace std;
int cr[MAXN<<2];
bool xr[MAXN<<2],vis[MAXN];
void fx(int u)
{
	if(cr[u]!=-1) cr[u]^=1;
	else xr[u]^=1;
}
void pushdown(int u)
{
	if(cr[u]!=-1) cr[u<<1]=cr[u<<1|1]=cr[u],xr[u<<1]=xr[u<<1|1]=0, cr[u]=-1; 
	//cr[u]=-1 这一语句的解释： 
	//因为要modify下面的子树（即更小的区间），无论此大区间是否会“鱼龙混杂”，但， 
	//此处改为cr[u]=-1即不会影响答案（询问时只需要到较下层的线段树节点去找答案就好了）
	//同时又规避了pushup。
	else if(xr[u]) fx(u<<1),fx(u<<1|1),xr[u]=0;
}
void modify(int u,int l,int r,int al,int ar,char op)
{
	if(al<=l&&r<=ar)
	{
		if(op=='U') cr[u]=1,xr[u]=0;
		else if(op=='D') cr[u]=0,xr[u]=0;
		else if(op=='C'||op=='S') fx(u);
		return;
	}
	pushdown(u);
	int mid=(l+r)>>1;
	if(al<=mid) modify(lson,al,ar,op);
	else if(op=='I'||op=='C') cr[u<<1]=xr[u<<1]=0;
	if(mid<ar) modify(rson,al,ar,op);
	else if(op=='I'||op=='C') cr[u<<1|1]=xr[u<<1|1]=0;
}
void query(int u,int l,int r)
{
	if(cr[u]==1) {for(int i=l;i<=r;i++) vis[i]=1; return;}
	else if(cr[u]==0) return;
	pushdown(u);
	int mid=(l+r)>>1;
	query(lson);
	query(rson);
}
int main()
{
	cr[1]=xr[1]=0;
	char op,l,r; int a,b;
	while(~(scanf("%c %c%d,%d%c
",&op,&l,&a,&b,&r)))
	{
		a<<=1;b<<=1;                                  //解决区间开闭问题 
		if(l=='(') a++; if(r==')') b--;
		if(a>b) {if(op=='I'||op=='C') cr[1]=xr[1]=0;} //T 为空集时的处理
		else modify(1,0,MAXN,a,b,op); 
	}
	query(1,0,MAXN);
	int s=-1,e; bool f=0;
	for(int i=0;i<=MAXN;i++)
	{
		if(vis[i]) {if(s==-1) s=i; e=i;}
		else 
		{	
			if(s!=-1)
			{
				if(f) printf(" "); f=true;
				printf("%c%d,%d%c",s&1==1?'(':'[',s>>1,e+1>>1,e&1==1?')':']');
				s=-1;
			}	
		}
	}
	if(!f)printf("empty set");
	return 0;
}

●hdu 1542 Atlantis(扫描线面积并)

○线段树的扫描线面积并,如今总算是入门了。

○没什么题解。。。

○贴上代码，当作模板，算是一种记录。

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 2222
#define lson u<<1,l,mid
#define rson u<<1|1,mid+1,r 
using namespace std;
struct seg{
	double x1,x2,y;
	int p;
}s[250];
int cnt[MAXN<<2];
double sum[MAXN<<2],x[MAXN],ans;
bool cmp(seg a,seg b) {return a.y<b.y;}
void pushup(int u,int l,int r)
{
	if(cnt[u]) sum[u]=x[r+1]-x[l];       //若[l-r]区间全部被覆盖，就直接计算 
	//若[l-r]区间未被全部被覆盖
	else if(l==r) sum[u]=0;				//底层处理 
	else sum[u]=sum[u<<1]+sum[u<<1|1]; //............
}
void modify(int u,int l,int r,int al,int ar,int p)
{
	if(al<=l&&r<=ar)
	{
		cnt[u]+=p;
		pushup(u,l,r);
		return;
	}
	int mid=(l+r)>>1;
	if(al<=mid) modify(lson,al,ar,p);
	if(mid<ar) modify(rson,al,ar,p);
	pushup(u,l,r);
}
int main()
{
	int n,cas=1,snt,lnt;
	while(1)
	{
		scanf("%d",&n);
		if(n==0) break;
		lnt=snt=0;
		ans=0;
		double a,b,c,d;
		for(int i=1;i<=n;i++)	
		{
			scanf("%lf%lf%lf%lf",&a,&b,&c,&d);
			s[++snt]=(seg){a,c,b,1};
			s[++snt]=(seg){a,c,d,-1};
			x[++lnt]=a; x[++lnt]=c;
		}
		sort(x+1,x+lnt+1);
		sort(s+1,s+snt+1,cmp);
		int m=1,l,r; 
		for(int i=2;i<=lnt;i++) if(x[i]!=x[i-1]) x[++m]=x[i];
		for(int i=1;i<=snt;i++)
		{
			l=lower_bound(x+1,x+m+1,s[i].x1)-x;
			r=lower_bound(x+1,x+m+1,s[i].x2)-x-1;//●●●●巧妙的减一 
			modify(1,1,m,l,r,s[i].p); 
			ans+=sum[1]*(s[i+1].y-s[i].y);
		}//循环完后，相关数组已清空
		printf("Test case #%d
Total explored area: %.2lf

",cas++,ans);
	}
	return 0;
}

●hdu 1828 Picture（扫描线周长并）

○和面积并差不多，但因为要求出和扫描线垂直的边的长度（即侧边），所以要多维护点东西来记录每次有几条侧边。

○特别注意排序的顺序与出边和入边有关了。

○模板来了：

#include<cstdio>
#include<cstring>
#include<iostream>
#include<algorithm>
#define MAXN 22222
#define lson u<<1,l,mid
#define rson u<<1|1,mid+1,r 
using namespace std;
struct seg{
	double x1,x2,y;
	int p;
}s[MAXN];
int cnt[MAXN<<2],bum[MAXN<<2];
int sum[MAXN<<2],x[MAXN],ans;
bool lb[MAXN<<2],rb[MAXN<<2];
bool cmp(seg a,seg b) {return a.y==b.y?a.p>b.p:a.y<b.y;}
void pushup(int u,int l,int r)
{
	if(cnt[u]) //若[l-r]区间全部被覆盖，就直接计算 
	{
	sum[u]=r-l+1;       
	bum[u]=2;
	lb[u]=rb[u]=1;
	}
	//若[l-r]区间未被全部被覆盖
	else if(l==r) sum[u]=bum[u]=0,lb[u]=rb[u]=0;			//底层处理 
	else 
	{
		sum[u]=sum[u<<1]+sum[u<<1|1];
		lb[u]=lb[u<<1]; rb[u]=rb[u<<1|1];
		bum[u]=bum[u<<1]+bum[u<<1|1];
		if(rb[u<<1]&&lb[u<<1|1]) bum[u]-=2;
	}
}
void modify(int u,int l,int r,int al,int ar,int p)
{
	if(al<=l&&r<=ar)
	{
		cnt[u]+=p;
		pushup(u,l,r);
		return;
	}
	int mid=(l+r)>>1;
	if(al<=mid) modify(lson,al,ar,p);
	if(mid<ar) modify(rson,al,ar,p);
	pushup(u,l,r);
}
int main()
{
	int LL,RR,n,snt,lnt,lb,rb,last,ans=0;
	while(~scanf("%d",&n))
	{
		ans=snt=0;LL=10000,RR=-10000;
		int a,b,c,d;
		for(int i=1;i<=n;i++)	
		{
			scanf("%d%d%d%d",&a,&b,&c,&d);
			s[++snt]=(seg){a,c,b,1};
			s[++snt]=(seg){a,c,d,-1};
			LL=min(LL,a);
			RR=max(RR,c);
		}
		sort(s+1,s+snt+1,cmp);
		last=0; 
		for(int i=1;i<=snt;i++)
		{
			int l=s[i].x1,r=s[i].x2;
			modify(1,LL,RR-1,l,r-1,s[i].p);
			ans+=bum[1]* (s[i+1].y-s[i].y);
			ans+=abs(sum[1]-last);
			last=sum[1];
		}
		printf("%d
",ans);
	}
	return 0;
}

●Tips○总结几点（聪明人才看得到。。。）

1.对于线段树的区间题，在把输入指令转化为线段树的区间操作时，要让各种操作有尽可能多的一致性，能使用更多相同的函数，这样可以在很大程度上降低代码复杂度和查错时间。

2.扫描线时，离散化后任把点看成线段树的底层元素，未离散化则将单位线段看成线段树的底层元素。

3.打线段树时一定要谨慎又谨慎，尽量减少出错，不然查错令人绝望！！！！！！