1:引言
数据的处理主要分为两种:操作型数据处理和分析型数据处理,前者可以称为oltp,后者可以称为olap。
2:olap定义
联机分析处理的定义有以下几种:
olap是以海量数据为基础的复杂分析技术,支持各级管理决策人员从不同的角度,快速灵活地对数据仓库中的数据进行复杂查询
和多维分析处理,并且能以直观易懂的形式将查询和分析结果提供给决策人员,从而辅助各级管理人员作出正确的决策。
3:olap的特点
支持海量数据
支持复杂查询计算
多维分析
快速灵活
支持决策
4:olap与oltp的区别
olap与oltp是两类不同的应用,oltp是对数据库中数据的联机查询和增删改操作,它以数据库为基础;而olap适合以数据仓库为
基础的数据分析处理;
olap中历史的,导出的以及经过综合提炼的数据主要来自于oltp所依赖的底层数据库,olap数据较oltp数据需要多一步综合处理
或多维化操作。
数据的处理主要分为两种:操作型数据处理和分析型数据处理,前者可以称为oltp,后者可以称为olap。
2:olap定义
联机分析处理的定义有以下几种:
olap是以海量数据为基础的复杂分析技术,支持各级管理决策人员从不同的角度,快速灵活地对数据仓库中的数据进行复杂查询
和多维分析处理,并且能以直观易懂的形式将查询和分析结果提供给决策人员,从而辅助各级管理人员作出正确的决策。
3:olap的特点
支持海量数据
支持复杂查询计算
多维分析
快速灵活
支持决策
4:olap与oltp的区别
olap与oltp是两类不同的应用,oltp是对数据库中数据的联机查询和增删改操作,它以数据库为基础;而olap适合以数据仓库为
基础的数据分析处理;
olap中历史的,导出的以及经过综合提炼的数据主要来自于oltp所依赖的底层数据库,olap数据较oltp数据需要多一步综合处理
或多维化操作。
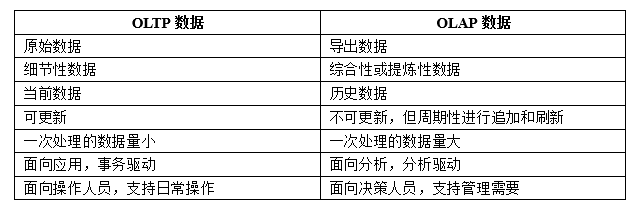
主要区别
oltp:原始数据,细节性数据,当前数据,可更新,一次性处理的数据量小,面向应用,事务驱动,面向操作人员,支持日常操作
olap:导出数据,综合性或提炼性数据,历史数据,不可更新,但周期进行追加或刷新,一次处理的数据量大,面向分析,分析驱
动,面向决策人员,支持管理需要。
5:多维数据模型的概念
a:定义
多维数据模型是olap中的一项核心技术。
多维数据模型是数据分析时用户的数据视图,是面向分析的数据模型,用于给分析人员提供多种观察的视角和面向分析的操作。
多维数据模型的数据结构可以用多维数组来表示,如:维度1,维度2...维度n。度量1,度量2...度量n
多维数据模型也可以用多维立方体来直观展现,其中维表示用户的观察视角,多维空间中的点表示度量的值。
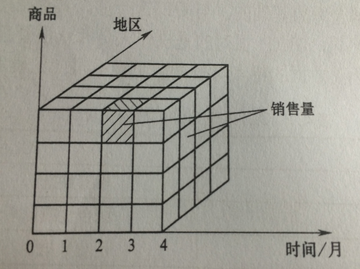
b:常用术语
1:维---维是人们观察事物的特定角度,是事物的某个属性,比如时间,地点,产品。每个维都有唯一的名称,比如时间维,地区
维,产品维。
2:维成员---维成员就是维的取值。如果一个维是多个层次的,那么维成员就是不同层次上的取值的组合。比如,地区维,维成员
就可以是“北京”,“上海”“杭州”等;而日期维包括年,月,日三个层次,那么它的为成员就是“2018年12月3日”,但并不是
每个层次上都有取值,比如“2018年8月”也可以是维成员。
3:维层---维是观察事物的角度,维层就是这个角度的细节程度,不同的细节程度对应着不同的维层。比如,日期维,可以从“年”
这一细节程度去观察,也可以从“季度”“月份”去观察,因此年,季度,月份等就是日期维的不同层次。层之间有一定的层次级别。
4:维层次---维层次是维层的不同划分。比如,日期维可以按照“年-季度-月”划分,也可以按照“年-星期-日”划分。两种划分规则
就是日期维的两个维层次。再比如产品维,可以按照产品,类型,种类划分,也可以按照承销商,代理商,制造商划分。
5:维属性---就是维成员所具有的特性,维属性可以在每个维成员上定义,也可以在维层上定义。如果在维层上定义,那么该维层
上的所有维成员都有这些属性,比如产品维的某一个成员“洗衣机”,他有一个洗涤重量的属性,这就是维属性。
6:度量---度量就是要分析的目标或对象。常见的度量值有销售量,供应量,利润等。度量一般有名称,数据类型,单位,计算公式
等属性。度量还可以分为可累计型和不可累计型。
7:数据方体---多维数据模型的空间展现就是数据数据方体,也称为多维立方体。一个数据方体由多个维度和度量组成,n维立方体
可以看作是由一系列的n-1维立方体组成。
8:数据单元---在一个数据立方体中,当每一个维上都有确定的维成员,那么就可以唯一确定多维空间中的一个点。一个数据单元可以
有多个度量值,比如一个三维立方体,有三个维度:日期维,地区维,时间维,那么2018-8-8,北京,冰箱,就可以确定一个数据单元
这个数据单元上的度量值就可以是利润,销售额,销售数量等。
6:常见的多维数据模型
常见的多维数据模型有星型模型,雪花模型,事实群模型。
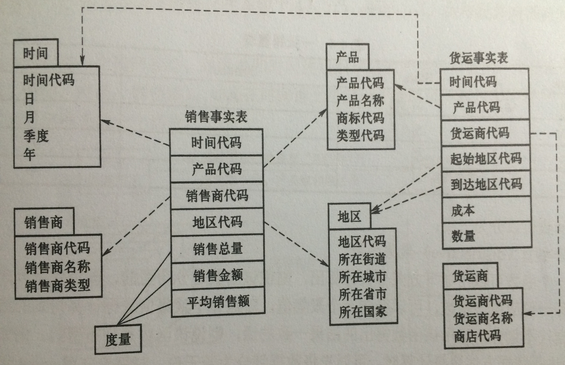
1:星型模型
星型模型是多维数据模型的基本结构,通常由位于中心的一张表和其周围的多张表组成。中心的表叫做事实表,周围的表叫做维度表。
事实表是用来存储事实的度量值和各种维度表的主码值。维度表用来保存维的信息,即每个维成员的属性信息和层次信息。事实表
通过维度表的主码与各维度表相连。
星型模型不支持维的层结构,每个维只有一个维表。如果一个维表有多个维层,那么所有的维层属性都必须放在这一个维表里面。
因此就会因为没有规范化而产生一定的冗余。
1:维---维是人们观察事物的特定角度,是事物的某个属性,比如时间,地点,产品。每个维都有唯一的名称,比如时间维,地区
维,产品维。
2:维成员---维成员就是维的取值。如果一个维是多个层次的,那么维成员就是不同层次上的取值的组合。比如,地区维,维成员
就可以是“北京”,“上海”“杭州”等;而日期维包括年,月,日三个层次,那么它的为成员就是“2018年12月3日”,但并不是
每个层次上都有取值,比如“2018年8月”也可以是维成员。
3:维层---维是观察事物的角度,维层就是这个角度的细节程度,不同的细节程度对应着不同的维层。比如,日期维,可以从“年”
这一细节程度去观察,也可以从“季度”“月份”去观察,因此年,季度,月份等就是日期维的不同层次。层之间有一定的层次级别。
4:维层次---维层次是维层的不同划分。比如,日期维可以按照“年-季度-月”划分,也可以按照“年-星期-日”划分。两种划分规则
就是日期维的两个维层次。再比如产品维,可以按照产品,类型,种类划分,也可以按照承销商,代理商,制造商划分。
5:维属性---就是维成员所具有的特性,维属性可以在每个维成员上定义,也可以在维层上定义。如果在维层上定义,那么该维层
上的所有维成员都有这些属性,比如产品维的某一个成员“洗衣机”,他有一个洗涤重量的属性,这就是维属性。
6:度量---度量就是要分析的目标或对象。常见的度量值有销售量,供应量,利润等。度量一般有名称,数据类型,单位,计算公式
等属性。度量还可以分为可累计型和不可累计型。
7:数据方体---多维数据模型的空间展现就是数据数据方体,也称为多维立方体。一个数据方体由多个维度和度量组成,n维立方体
可以看作是由一系列的n-1维立方体组成。
8:数据单元---在一个数据立方体中,当每一个维上都有确定的维成员,那么就可以唯一确定多维空间中的一个点。一个数据单元可以
有多个度量值,比如一个三维立方体,有三个维度:日期维,地区维,时间维,那么2018-8-8,北京,冰箱,就可以确定一个数据单元
这个数据单元上的度量值就可以是利润,销售额,销售数量等。
6:常见的多维数据模型
常见的多维数据模型有星型模型,雪花模型,事实群模型。
1:星型模型
星型模型是多维数据模型的基本结构,通常由位于中心的一张表和其周围的多张表组成。中心的表叫做事实表,周围的表叫做维度表。
事实表是用来存储事实的度量值和各种维度表的主码值。维度表用来保存维的信息,即每个维成员的属性信息和层次信息。事实表
通过维度表的主码与各维度表相连。
星型模型不支持维的层结构,每个维只有一个维表。如果一个维表有多个维层,那么所有的维层属性都必须放在这一个维表里面。
因此就会因为没有规范化而产生一定的冗余。

2:雪花模型
雪花模型是在星型模型的基础上发展而来的,每一个维度不再只有一张维度表,而是可以有多张维度表。雪花模型和星型模型的主要
区别在于:雪花模型会根据维层对维度表进行规范化。经过规范化的维表不仅易于存储,而且能节省空间,但是在查询时就需要比较
多的连接操作。因此,我们在处理时,可以将雪花模型和星型模型进行综合,对于较小的维度表仍然使用星型模型的不规范形式,对
于较大的维度表则使用雪花模型的规范形式。

3:事实群模型
事实群模型类似于星型模型,区别只是多张事实表之间可以共享同一张维度表。
事实群模型类似于星型模型,区别只是多张事实表之间可以共享同一张维度表。
7:常用的分析操作
1:多维分析基础---聚集函数
聚集就是对细节数据进行综合的过程。
最常用的五中聚集函数:求和(sum),计数(count),最大值(max),最小值(min),平均值(avg),求中间值(median),
排序(rank);
2:切片:slice
就是在数据方体的某一维上选定一个维成员的动作,即限定多维数组某一维度只取一个特定值。
比如地区维,选定“北京”这一个维成员,这样就得到一个切片。
3:切块:dice
就是在数据方体的某一维上选定某个区间的全部维成员的动作,即限定多维数组某一个维度只取一定区间的值。
比如地区维,选定“北京”“上海”“广州”,这样就得到一个切块。当这一区间只有一个维成员时,就得到一个切片。因此
切块可以由多个切片操作叠合而成。
4:旋转
改变数据方体维的次序的动作称为旋转,旋转操作对数据不做任何改变,只是改变立方体摆放的视角。
5:下钻
下钻操作就是在某个分析的过程中,用户可能需要从更多的维或者某个维的更细层次上观察数据,这时候就需要通过下钻操作
来实现。比如将日期维从季节层次下钻到月份层次,下钻前用户只能看到季度数据,而下钻后就可以看到月份数据。
下钻操作主要有两种类型:一是现有的维下钻取更细节一层的数据,比如日期维上的季度数据下钻到月份数据
二是增加更多的维,比如现在只分析了三个维度的数据,但是问题仍然无法解决,这时候就需要更多
维度的数据。
6:上卷
上卷操作是相对下钻操作而言的,下钻可以看到更多更细节数据,因此上卷操作就是看到更少更综合数据。因此,上卷操作也
分为两种,一是上卷到更高层次的数据,另一种是减少维度。
1:多维分析基础---聚集函数
聚集就是对细节数据进行综合的过程。
最常用的五中聚集函数:求和(sum),计数(count),最大值(max),最小值(min),平均值(avg),求中间值(median),
排序(rank);
2:切片:slice
就是在数据方体的某一维上选定一个维成员的动作,即限定多维数组某一维度只取一个特定值。
比如地区维,选定“北京”这一个维成员,这样就得到一个切片。
3:切块:dice
就是在数据方体的某一维上选定某个区间的全部维成员的动作,即限定多维数组某一个维度只取一定区间的值。
比如地区维,选定“北京”“上海”“广州”,这样就得到一个切块。当这一区间只有一个维成员时,就得到一个切片。因此
切块可以由多个切片操作叠合而成。
4:旋转
改变数据方体维的次序的动作称为旋转,旋转操作对数据不做任何改变,只是改变立方体摆放的视角。
5:下钻
下钻操作就是在某个分析的过程中,用户可能需要从更多的维或者某个维的更细层次上观察数据,这时候就需要通过下钻操作
来实现。比如将日期维从季节层次下钻到月份层次,下钻前用户只能看到季度数据,而下钻后就可以看到月份数据。
下钻操作主要有两种类型:一是现有的维下钻取更细节一层的数据,比如日期维上的季度数据下钻到月份数据
二是增加更多的维,比如现在只分析了三个维度的数据,但是问题仍然无法解决,这时候就需要更多
维度的数据。
6:上卷
上卷操作是相对下钻操作而言的,下钻可以看到更多更细节数据,因此上卷操作就是看到更少更综合数据。因此,上卷操作也
分为两种,一是上卷到更高层次的数据,另一种是减少维度。