1使用BN进行数据归一化的原因
a) 神经网络学习过程本质就是为了学习数据分布,一旦训练数据与测试数据的分布不同,那么网络的泛化能力也大大降低;
b) 另外一方面,一旦每批训练数据的分布各不相同(batch 梯度下降),那么网络就要在每次迭代都去学习适应不同的分布,这样将会大大降低网络的训练速度.
2.BN概述
a) 实质。在网络的每一层输入的时候,又插入了一个归一化层,也就是先做一个归一化处理,然后再进入网络的下一层。BN操作层,它位于X=WU+B激活值获得之后,非线性函数变换之前
b) 数据预处理之白话预处理
真白化处理后数据满足条件:a、特征之间的相关性降低,这个就相当于pca;b、数据均值、标准差归一化,也就是使得每一维特征均值为0,标准差为1。
但是白话处理要满足上述两个条件的话,计算量特别大。
3.BN算法核心思想
a) 归一化公式(伪白化)
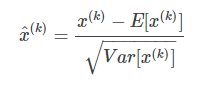
可计算,该公式所有x(k)的估计值的均值为0,方差为1,此时均为标准正太分布N~(0,1)。
b)数据分布恢复
因为上公式强制将网络中间某一层学习到特征数据给我归一化处理、标准差也限制在了1,把数据变换成分布于s函数的中间部分,损害了该层网络所学到的特征。数据恢复使用下面的公式:

可以推到的y(k)=x(k).
则BN网络前向传导公式为:
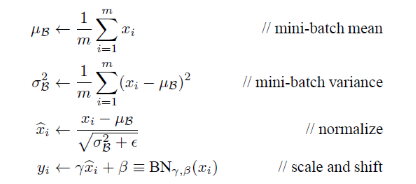
x的估计值服从标准正太分布,则x经过线性变换后的y,仍然服从正太分布,可计算y的均值为(beta谐音),方差为(gama谐音)。
4.使用BN的优点
a) 快速训练收敛。可以选择比较大的初始学习率。对于学习率、参数初始化、权重衰减系数、Drop out比例等,不需要那么刻意的慢慢调整参数。
b) 不用处理过拟合中drop out、L2正则项参数的选择问题,采用BN算法后,可以移除这两项了参数,或者可以选择更小的L2正则约束参数了,因为BN具有提高网络泛化能力的特性;
c) 不需要使用使用局部响应归一化层。BN中也会对数据进行归一化。
d) 在训练的时候可以把训练数据彻底打乱(防止每批训练的时候,某一个样本都经常被挑选到),文献说这个可以提高1%的精度。
4.BNN模型思想
从第一层一直到最后一层,需要说明的是除了最后一个隐含层到输出层的连接权值和激活是实参外,其他的权值为二值化参数。Binarize为二值化函数。
4.1前向传播阶段
在一个神经元处需要做的操作有:二值化连接权值—>权值与输入相乘-->BatchNorm(BatchNormalization)得到这一层的激活值ak—>将 ak二值化。即:在隐含层计算阶段所有的值都为二值化后的结果。

4.2反向传播阶段

先求解第k+1层的误差值:
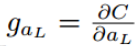
然后对二值操作层求梯度,根据链式法则,求BN层的梯度,求二值化后的W的梯度。
4.3参数更新

根据上面计算的梯度更新参数。其中,在求权值(W)梯度的时候是对二值化后的权值求梯度,但是权值更新的时候,是利用上面求得的权值梯度对实数型的权值进行更新。
5.二值化方法
二值化的两种方法:
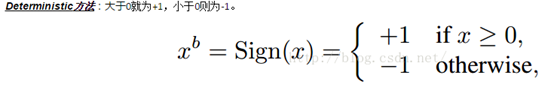

clip(x,min,max)函数使数据限制再min与max之间,小于min的都等于min,大于max的都等于max.
由于当计算机生成随机数的时候非常耗时,出于初衷加速考虑,所以一般以第一种方法进行实施。
但第一种方法函数的倒数处处为0,并不能进行梯度反向传播。另外梯度具有累加效果,即梯度都带有一定的噪音,而噪音一般认为是服从正态分布的,所以,多次累加梯度才能把噪音平均消耗掉。
对第一种方法的函数进行简单改进:
在前向传播阶段,对weights和activation的二值化相当于对网络的参数引入噪声,可以提高网络抗过拟合的能力。另外这可以看做是dropout的一种变形。Dropout是将激活值的一般变成0,从而造成一定的稀疏性,而二值化则是将另一半变成1,从而可以看做是进一步的dropout。