题目要求:
输入一个数组,用算法实现输出和最大的连续子数组的和,时间复杂度O(n)。
分析思路:
这个问题是典型的动态规划问题,动态规划对于我来说市纪委陌生的,通过了解,动态规划的思想是这样的:
如果用函数f(i)表示以第i个数字结尾的子数组的最大和,那么我们需要求出max(f[0...n])。我们可以给出如下递归公式求f(i)

这个公式的意义:
- 当以第(i-1)个数字为结尾的子数组中所有数字的和f(i-1)小于0时,如果把这个负数和第i个数相加,得到的结果反而不第i个数本身还要小,所以这种情况下最大子数组和是第i个数本身。
- 如果以第(i-1)个数字为结尾的子数组中所有数字的和f(i-1)大于0,与第i个数累加就得到了以第i个数结尾的子数组中所有数字的和
实验代码:
1 //动态规划求最大连续子数组和 2 #include<iostream> 3 using namespace std; 4 int FindGreatestSumOfSubArray(int arry[], int len, int c[]) 5 { 6 c[0] = arry[0]; 7 int start, end;//记录开始位和结束位 8 int temp = 0; 9 int maxGreatSum = -100;//设置一个相当小的值来保证接下来计算。 10 for (int i = 1; i<len; i++) 11 { 12 if (c[i - 1] <= 0) 13 { 14 c[i] = arry[i]; 15 temp = i;//记录位置i 16 } 17 else 18 c[i] = arry[i] + c[i - 1]; 19 if (c[i]>maxGreatSum)// 20 { 21 maxGreatSum = c[i]; 22 start = temp;//开始位 23 end = i;//结束位 24 } 25 } 26 //输出c[i]和最大子序列位置 27 for (int i = 0; i<len; i++) 28 cout << c[i] << " "; 29 cout << endl; 30 31 cout << "最大子序列位置:" << start << "--" << end << endl; 32 return maxGreatSum; 33 } 34 //控制输入输出,调用函数FindGreatestSumOfSubArray完成结果输出 35 int main() 36 { 37 int i,n; 38 int A[50] = {}; 39 int B[50] = {}; 40 cout << "请输入数组中数的个数:"<<endl; 41 cin >> n; 42 cout << "请依次输入数组中的数:"<< endl; 43 for (i = 0; i != n; ++i) 44 cin >> A[i]; 45 FindGreatestSumOfSubArray(A, n,B); 46 47 }
实验截图:
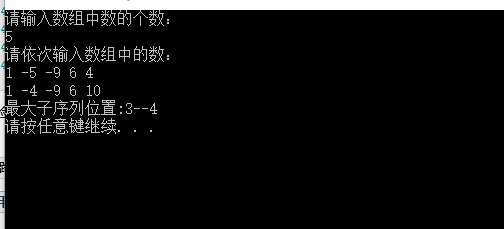

实验结果检测正常,符合题目要求,在细节设置上有所涉及。
实验总结:
这次实验给我最大的感觉是脑洞大开,让我们脱离了以往的较为简单的想法套路,对于动态规划的问题也有很大的理解。这是一个对待这类问题的捷径和极为优化的方案。