题目链接:http://poj.org/problem?id=1733
题目大意:有一个很长很长含有01的字符串,长度可达1000000000,首先告诉你字符串的长度n,再给一个m,表示给你m条信息,接下来的m行每行包含x,y,even/odd,表示区间【x,y】中1的个数,even为偶数,odd为奇数。判断前几条是对的,也就是说假设k+1条信息与前面相互矛盾,就输出k,说明前k条正确。
例:
Sample Input
10
5
1 2 even
3 4 odd
5 6 even
1 6 even
7 10 odd
Sample Output
3
解题思路:wa了n多次,但是思路正确了,字符串长度太大,开不了那么大的数组,看了题解才知道还可以离散化。
如果不会离散化,就看下这个博客:https://blog.csdn.net/xiangaccepted/article/details/73276826
不过我没有用那里的方法离散化,直接看大佬的,用map离散化挺方便的,因为这些数本身大小不重要,而重要的是他们的相对关系,所以可以进行离散化处理。
做法就是运用带权并查集,区间【x,y】中1的个数为偶数时,说明前x-1个数和前y个数中1的个数奇偶性相同,反之区间【x,y】1的个数为奇数,说明前x-1个数和前y个数中1的个数奇偶性不同。我们就可以用一个关系数组relation【】存储该节点与其父亲节点的奇偶性是否一致(0相同,1不相同)。
然后问题就在于更新它们的关系域了
第一个是查找的时候,还要进行路径压缩,所以节点的关系域要更新。
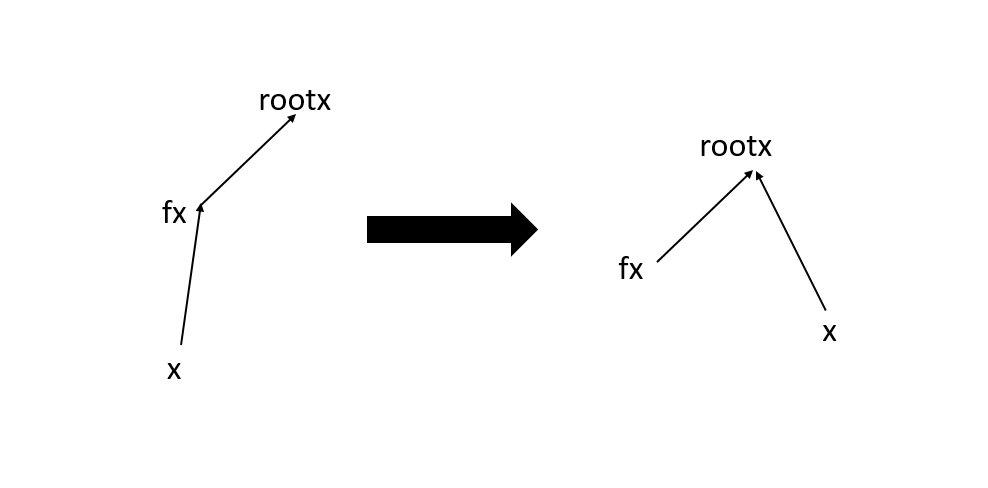
假设做图是路径压缩前,右图是路径压缩后,我们把可以简单的对他们的关系进行枚举,就可以找到他们的关系了
relation【x】 relation【fx】 更新后relation【x】
0 0 0
0 1 1
1 0 1
1 1 0
很明显就是异或的关系,所以可以得到relation[x]=(relation[x]+relation[par[x]])%2,也就是relation[x]=relation[x]^relation[par[x]].
还有就是当两个元素的根不一样时需要合并两个集合,假如是将x所在集合的根rootx合并到y所在的集合的根rooty,这时候rootx的关系域也要进行更新,因为原本它的父亲节点是它自己,后来变成了rooty。
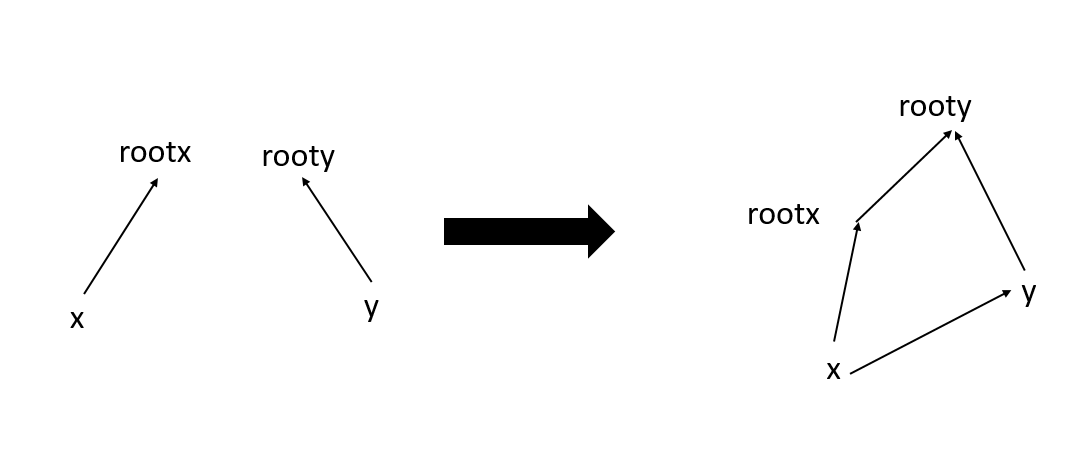
从左图变成右图,再作了一条辅助线,x->y便于理解下,我们要求的更新后relation【rootx】与它的父亲节点rooty的关系
看到这图我们是不是可以想想可不可以用向量去做呢?事实证明是可以的
根据向量的知识我们可以知道:rootx->rooy=x->y+y->rooty-x->rootx
这不就等价于我们的:relation[rootx]=x与y的关系d+relation[y]-relation[x]
为了保证不超出我们的关系的范围(【0,1】)所以我们的式子为relation[fx]=(d+relation[y]-relation[x]+2)%2(加2保证结果不为负数)
还有最后一个就是当x和y的根节点已经相同时,我们怎么判断是否与前面的信息有矛盾呢?
其实就是我们查找时更新关系域是一样的。
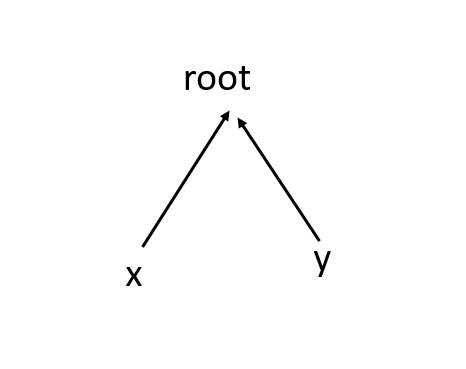
relation【x】 relation【y】 d(x与y的关系)
0 0 0
0 1 1
1 0 1
1 1 0
直接判断relation[x]^relation[y]==d
如果不等于肯定是有矛盾的。
思路基本就这样,其他也没什么了,看代码吧。
这应该是我写的最详细的一篇解题报告了。。。
附上代码:
1 #include<iostream>
2 #include<cstdio>
3 #include<map>
4 #include<cstring>
5 using namespace std;
6 int par[5005*2],relation[2*5005];
7 int ans,q;
8
9 void init(int x)
10 {
11 for(int i=0;i<=x;i++)
12 {
13 par[i]=i;
14 relation[i]=0;
15 }
16 }
17
18 int find(int x)
19 {
20 if(x!=par[x])
21 {
22 int temp=find(par[x]);
23 relation[x]=(relation[x]+relation[par[x]])%2; //更新relation[x]
24 par[x]=temp;
25 }
26 return par[x];
27 }
28
29 void unite(int x,int y,int d,int cnt) //d是x和y的关系,cnt是第几条消息
30 {
31 int fx=find(x);
32 int fy=find(y);
33 if(fx==fy)
34 {
35 if(relation[x]^relation[y]!=d&&q==0)
36 {
37 ans=cnt-1; //第cnt条消息矛盾,说明前cnt-1条消息对的
38 q++;
39 }
40 return;
41 }
42 else
43 {
44 par[fx]=fy;
45 relation[fx]=(d+relation[y]-relation[x]+2)%2;
46 }
47 }
48
49 bool same(int x,int y)
50 {
51 return find(x)==find(y);
52 }
53
54 signed main()
55 {
56 int n,m;
57 map<int,int> mp; //用于离散化
58 while(cin>>n>>m)
59 {
60 mp.clear();
61 init(2*5005);
62 ans=m;
63 int count=1;
64 int k=1,q=0;
65 while(m--)
66 {
67 int a,b,d;
68 char s[10];
69 cin>>a>>b>>s;
70 if(!mp[a-1])
71 mp[a-1]=count++;
72 if(!mp[b])
73 mp[b]=count++;
74 if(s[0]=='e') d=0; //偶数,x-1和y奇偶性相同
75 else d=1;
76 unite(mp[a-1],mp[b],d,k); //k是记录第几条消息
77 k++;
78 }
79 cout<<ans<<endl;
80 }
81 return 0;
82 }