ACM-ICPC 2018 南京赛区网络预赛 J题Sum(线性筛素数)

题目链接：https://nanti.jisuanke.com/t/30999

参考自博客：https://kuangbin.github.io/2018/09/01/2018-ACM-ICPC-Nanjing-online-J/

题目中文：

•  1000毫秒
•  512000K

无方形整数是一个整数，除了1以外的任何平方数都不可分 这个数。例如，6 = 2 *3，6=2*3，6是无方形整数，但12 = 2 ^ 2*3，,因为2 ^ 2是正方形数。有些整数可以分解为两个无方形整数的乘积，可能有多种分解方式。例如，6=1·6=6·1=2·3=3·2，n=a*b和n=b*a被认为是不同的。f （n ）是分解方式的数量n=a*b。问题在于计算

输入

第一行包含一个整数 ，表示的测试用例的数量。

对于每个测试用例，第一行有一个整数 

产量

对于每个测试用例，打印答案 

暗示

 

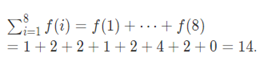
样例输入复制

2

5

8

样例输出复制

8

14

 解题思路：首先我们对f（n）分析，我们知道对于任意一个数，我们都可以把他拆分成若干素因子乘积的形式如f(n)=p^x+q^y+……r^z，如果f（n）的素因子分解式子中，某个素因子的指数大于二，则f(n)就一定为0；比如f(8)=f(2^3)=0;

如果f(n)非0，则f(n)的素因子的指数只能为1或者2了，如果该素因子的指数为1，则对结果的贡献度为2（即其余素因子分成两部分，可加入任意一边），如果该素因子的指数为1，则对结果的贡献度为1（其余素因子分成两部分，一边一个）；

所有如果单独求一个f(n)的话，只需要对n进行素因素分解。

但是现在需要求1∼2×10^7的f(n), 我们需要进行递推。

假如我们知道n的最小素因子是p的话，而且p的指数是x的话，即n=y*p^x.

那么很显然，如果x == 1, 那么f(n)=2×f(y), 如果x == 2, 那么f(n)=f(y), 如果x > 2, 那么f(n)=0.

然后这里就这要用线性筛素数了，而筛素数的同时记录每个最小的素因子。

附上代码：

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const ll maxn=2e7;
int prime[maxn+7],minprime[maxn+7];
ll cnt[maxn+7];
//线性筛素数
void getprime()
{
    memset(prime,0,sizeof(prime));
    int tot=0;
    for(int i=2;i<=maxn;i++)
    {
        if(!prime[i])
        {
            prime[tot++]=i;
            minprime[i]=i;
        }
        for(int j=0;j<tot&&i*prime[j]<=maxn;j++)
        {
            prime[i*prime[j]]=1;
            minprime[i*prime[j]]=prime[j];
            if(i%prime[j]==0)
            break;
        }
    }
}

int main()
{
    getprime();
    cnt[1]=1;
    for(int i=2;i<=maxn;i++)
    {
        int x=minprime[i];  //最小素因子
        if(i%(x*x*x)==0) cnt[i]=0;  //最小素因子指数大于2
        else if(i%(x*x)==0) cnt[i]=cnt[i/(x*x)]; //最小素因子指数等于2
        else cnt[i]=2*cnt[i/x];  //最小素因子指数为1
    }
    for (int i=2;i<=maxn;i++)
        cnt[i]+=cnt[i-1];
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        printf("%lld
",cnt[n]);
    }
    return 0;
}