本文参考自 Wearry 在集训的讲解《DP及其优化》。
简介
凸优化解决的是一类选择恰好 (K) 个某种物品的最优化问题 , 一般来说这样的题目在不考虑物品数量限制的条件下会有一个隐性的图像 , 表示选择的物品数量与问题最优解之间的关系 .
每个点就是选了 (K) 个物品的最优Dp值。(答案)也就是 ((K, f(K))) 。
问题能够用凸优化解决还需要满足图像是凸的 , 直观地理解就是选的物品越多的情况下多选一个物品 , 最优解的增长速度会变慢 .
解法
解决凸优化类型的题目可以采用二分的方法 , 即二分隐性凸壳上最优值所在点的斜率 , 然后忽略恰好 (K) 个的限制做一次原问题 .
这样每次选择一个物品的时候要多付出斜率大小的代价 , 就能够根据最优情况下选择的物品数量来判断二分的斜率与实际最优值的斜率的大小关系 .
理论上这个斜率一定是整数 , 由于题目性质可能会出现二分不出这个数的情况 , 这时就需要一些实现上的技巧保证能够找到这个最优解 .
因为相邻两个点横下标差 (1) (多选一个),纵坐标都是整数。(对于大部分的题目最优解都是整数)。
这个也就是 CTSC 上讲的 带权二分 啦。
例题
UOJ #104. 【APIO2014】Split the sequence
题意
将一个长为 (n) 的序列分成 (k+1) 个块,每次分割得到分割处 左边的和 与 右边的和 乘积的分数。
保证序列中每个数非负。最后需要最大化分数,需要求出任意一组方案。
(2 le n le 10^5, 1 le k le min {n - 1, 200})
题解
直接做斜率优化是 (O(nk)) 的,那个十分 简单 ,注意细节就行了。可以参考 我的代码 。
虽然已经过了这题了,但是有更好的做法。也就是对于 (k le n - 1) 也就是 (k,n) 同级的时候有更好的做法。
考虑前面讲的凸优化,我们考虑二分那个斜率,也就是分数的增长率。
假设二分的值为 (mid) ,相当于转化成没有分段次数的限制,但是每次分段都要额外付出 (mid) 的代价 , 求最大化收益的前提下分段数是多少 .
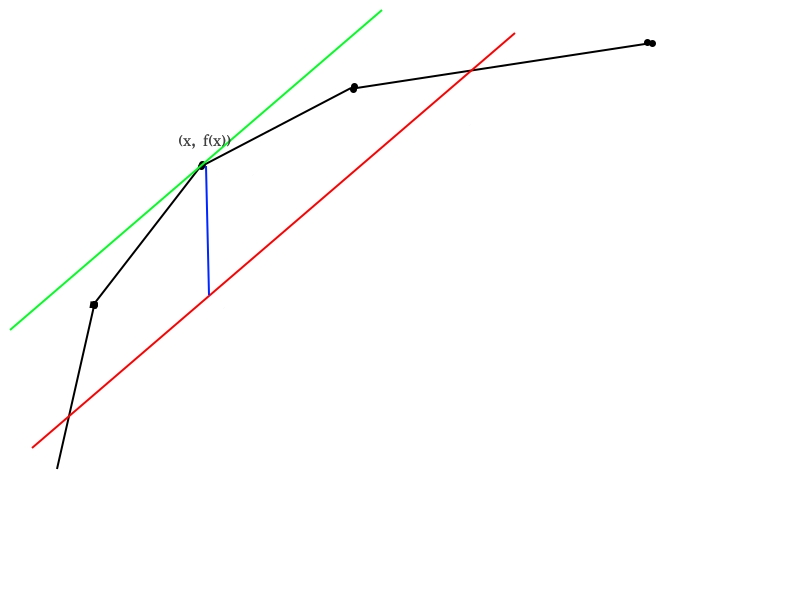
具体化来说,就例如上图,那个上凸壳就是答案的图像,我们当前二分的那个斜率的直线就是那条红线。
我们当前是最大化 (f(x) - x imes mid) 。
那么我们考虑把红线向上不断平移,那么最后接触到的点就是这条直线与上凸壳的切点。此时答案最大。
那么我们算出的分段数就是 (x) ,也就是切点的下标。然后比较一下 (x) 与 (k) 的关系,判断应该向哪边移动。
然后最后得到斜率算出的方案就是最优方案了。
我没有写 但听说细节特别多,输出方案很恶心。如果想写的话,可以看下 UOJ 最快的代码,来自同届大佬 yww 的。
这个复杂度就是 (O(n log w)) 的,十分优秀。
CF739E Gosha is hunting
题意
你要抓神奇宝贝! 现在一共有 (n) 只神奇宝贝。 你有 (a) 个『宝贝球』和 (b) 个『超级球』。 『宝贝球』抓到第 (i) 只神奇宝贝的概率是 (p_i) ,『超级球』抓到的概率则是 (u_i) 。 不能往同一只神奇宝贝上使用超过一个同种的『球』,但是可以往同一只上既使用『宝贝球』又使用『超级球』(都抓到算一个)。 请合理分配每个球抓谁,使得你抓到神奇宝贝的总个数期望最大,并输出这个值。
(n le 2000)
题解
不难发现用的球越多,期望增长率越低。这是很好理解的,一开始肯定选更优的神奇宝贝球,然后再选较劣的神奇宝贝球。
这就意味着这个隐性的图像是上凸的,我们可以类似于上题的套路,我们二分那个斜率。
然后我们就可以忽略个数的限制了。但此处这里有两个变量,那么我们二分套二分就行了。
假设当前二分的是 (mid) ,那么我们每次选择一个神奇宝贝球就要付出 (mid) 的代价。
然后求出最大化收益时需要选多少个神奇宝贝球就行了,这个可以用一个很容易的 dp 求出。
但注意两个同时选的时候,概率应该是 (p_a + p_b - p_a imes p_b) 。
但此时有一个重要的细节,就是二分到最后斜率求出的答案不一定是正确的。
但是在其中如果我们二分到 最优解要选的球和我最后用的球一样的话,那么这样就是一个最优的可行解。
至于原因?无可奉告!
似乎是可能有三点共线的情况,此时选的个数有问题。并且最后需要用给你的个数,不能用求出的个数。
代码
具体看看代码。。。反正我也不知道为什么这么多特殊情况。
#include <bits/stdc++.h>
#define For(i, l, r) for(register int i = (l), i##end = (int)(r); i <= i##end; ++i)
#define Fordown(i, r, l) for(register int i = (r), i##end = (int)(l); i >= i##end; --i)
#define Set(a, v) memset(a, v, sizeof(a))
#define Cpy(a, b) memcpy(a, b, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define DEBUG(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
inline bool chkmax(double &a, double b) {return b > a ? a = b, 1 : 0;}
inline int read() {
int x = 0, fh = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') fh = -1;
for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
return x * fh;
}
void File() {
#ifdef zjp_shadow
freopen ("E.in", "r", stdin);
freopen ("E.out", "w", stdout);
#endif
}
const double eps = 1e-10;
const int N = 2010;
int n, a, b;
double pa[N], pb[N]; int usea, useb; double f;
void Calc(double costa, double costb) {
f = 0; usea = useb = 0;
For (i, 1, n) {
int cura = 0, curb = 0; double res = 0;
if (chkmax(res, pa[i] - costa)) cura = 1, curb = 0;
if (chkmax(res, pb[i] - costb)) cura = 0, curb = 1;
if (chkmax(res, pa[i] + pb[i] - pa[i] * pb[i] - (costa + costb))) cura = curb = 1;
usea += cura; useb += curb; f += res;
}
}
int main () {
File();
n = read(); a = read(); b = read();
For (i, 1, n) scanf("%lf", &pa[i]);
For (i, 1, n) scanf("%lf", &pb[i]);
double la = 0, ra = 1, lb, rb;
while (la + eps < ra) {
double mida = (la + ra) / 2.0; lb = 0, rb = 1;
while (lb + eps < rb) {
double midb = (lb + rb) / 2.0;
Calc(mida, midb);
if (useb == b) {lb = midb; break; }
if (useb < b) rb = midb; else lb = midb;
}
if (usea == a) { la = mida; break; }
if (usea < a) ra = mida; else la = mida;
}
Calc(la, lb);
printf ("%.10lf
", f + la * a + lb * b);
return 0;
}
LOJ #2478. 「九省联考 2018」林克卡特树
题意
请点上面链接qwq 题意很好理解的。(但要认真看题)
题解
题意等价于,恰好选 (k) 条链, 使得他们的长度和最大。
我们同样可以使用凸优化对于这个来进行优化。
二分那个斜率 (mid) ,每次选择多一条链就要减去 (mid) ,最后求使得答案最优的时候,需要分成几段。
但这些都不是重点,重点是如何求出答案最优的时候有多少段。
我们令 dp[u][0/1/2] 为 (u) 这个点,向子树中延伸出 (0,1,2) 条链。
转移的话,枚举一下它从和哪个儿子的链相连,计算一下分的段数即可。
为了方便计算段数,在链的底部统计上段数,所以合并两条链的时候需要减去一段,并且把权值加回来 (mid) 。
记得要统计上别的子树的答案!!先挂下 (dp) 的代码吧。
利用
std :: pair<ll, int>写的更加方便,第一维表示答案,第二维表示段数。
typedef pair<ll, int> PLI;
#define res first
#define num second
#define mp make_pair
inline PLI operator + (const PLI &lhs, const PLI &rhs) {
return mp(lhs.res + rhs.res, lhs.num + rhs.num);
}
PLI f[N][3]; ll del;
void Dp(int u = 1, int fa = 0) {
f[u][0] = mp(0, 0);
f[u][1] = mp(- del, 1);
f[u][2] = mp(- inf, 0);
for (register int i = Head[u]; i; i = Next[i]) {
register int v = to[i]; if (v == fa) continue ; Dp(v, u);
PLI tmp = max(f[v][0], max(f[v][1], f[v][2]));
chkmax(f[u][2], f[u][2] + tmp);
chkmax(f[u][2], f[u][1] + f[v][1] + mp(val[i] + del, -1));
chkmax(f[u][1], f[u][1] + tmp);
chkmax(f[u][1], f[u][0] + f[v][1] + mp(val[i], 0));
chkmax(f[u][1], f[u][0] + f[v][0] + mp(- del, 1));
chkmax(f[u][0], f[u][0] + tmp);
}
}
然后又会有三点共线的情况,也就是对于选择连续几个答案都是相同的。
我们发现,利用 std :: pair<ll, int> 的运算符 < ,会在第一维答案相同时优先第二维段数小的在前。
所以我们更新答案的时候就需要在 (use > k) 也就是需求大于供给 通货膨胀 的时候进行更新,不然答案可能更新不到。
如果 (use = k) 那么就可以直接退出输出答案就行啦。
代码
#include <bits/stdc++.h>
#define For(i, l, r) for(register int i = (l), i##end = (int)(r); i <= i##end; ++i)
#define Fordown(i, r, l) for(register int i = (r), i##end = (int)(l); i >= i##end; --i)
#define Set(a, v) memset(a, v, sizeof(a))
#define Cpy(a, b) memcpy(a, b, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define DEBUG(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
typedef long long ll;
template<typename T> inline bool chkmax(T &a, T b) {return b > a ? a = b, 1 : 0;}
namespace pb_ds
{
namespace io
{
const int MaxBuff = 1 << 15;
const int Output = 1 << 23;
char B[MaxBuff], *S = B, *T = B;
#define getc() ((S == T) && (T = (S = B) + fread(B, 1, MaxBuff, stdin), S == T) ? 0 : *S++)
char Out[Output], *iter = Out;
inline void flush()
{
fwrite(Out, 1, iter - Out, stdout);
iter = Out;
}
}
inline int read()
{
using namespace io;
register char ch; register int ans = 0; register bool neg = 0;
while(ch = getc(), (ch < '0' || ch > '9') && ch != '-') ;
ch == '-' ? neg = 1 : ans = ch - '0';
while(ch = getc(), '0' <= ch && ch <= '9') ans = ans * 10 + ch - '0';
return neg ? -ans : ans;
}
};
using namespace pb_ds;
void File () {
#ifdef zjp_shadow
freopen ("2478.in", "r", stdin);
freopen ("2478.out", "w", stdout);
#endif
}
const int N = 3e5 + 1e3, M = N << 1;
int Head[N], Next[M], to[M], val[M], e = 0;
inline void add_edge(int u, int v, int w) {
to[++ e] = v; Next[e] = Head[u]; Head[u] = e; val[e] = w;
}
inline void Add(int u, int v, int w) {
add_edge(u, v, w); add_edge(v, u, w);
}
typedef long long ll;
const ll inf = 1e18;
typedef pair<ll, int> PLI;
#define res first
#define num second
#define mp make_pair
inline PLI operator + (const PLI &lhs, const PLI &rhs) {
return mp(lhs.res + rhs.res, lhs.num + rhs.num);
}
PLI f[N][3]; ll del;
void Dp(int u = 1, int fa = 0) {
f[u][0] = mp(0, 0);
f[u][1] = mp(- del, 1);
f[u][2] = mp(- inf, 0);
for (register int i = Head[u]; i; i = Next[i]) {
register int v = to[i]; if (v == fa) continue ; Dp(v, u);
PLI tmp = max(f[v][0], max(f[v][1], f[v][2]));
chkmax(f[u][2], f[u][2] + tmp);
chkmax(f[u][2], f[u][1] + f[v][1] + mp(val[i] + del, -1));
chkmax(f[u][1], f[u][1] + tmp);
chkmax(f[u][1], f[u][0] + f[v][1] + mp(val[i], 0));
chkmax(f[u][1], f[u][0] + f[v][0] + mp(- del, 1));
chkmax(f[u][0], f[u][0] + tmp);
}
}
int n, k, use; PLI ans;
void Calc(ll cur) {
ans = mp(-inf, 0); del = cur; Dp();
For (i, 0, 2) chkmax(ans, f[1][i]); use = ans.num;
}
ll Ans;
int main () {
File();
n = read(), k = read() + 1;
For (i, 1, n - 1) {
register int u = read(), v = read(), w = read(); Add(u, v, w);
}
ll l = -1e6, r = 8e7;
while (l <= r) {
ll mid = (l + r) >> 1;
Calc(mid);
if (use == k) return printf ("%lld
", ans.res + mid * k), 0;
if (use < k) r = mid - 1;
else l = mid + 1, Ans = ans.res + mid * k;
}
printf ("%lld
", Ans);
return 0;
}
LOJ #566. 「LibreOJ Round #10」yanQval 的生成树
题意
戳进去 >> #566. 「LibreOJ Round #10」yanQval 的生成树 。
题意简单明了 qwq
题解
首先,显然有 (mu) 是这些数的中位数。
然后我们就很容易想到考虑枚举中位数 (mid) ,然后在 (w_i < mid) (白边)与 (w_i ge mid) (黑边)分别选 (displaystyle lfloor frac{n - 1}{2} floor) 条边,组成最大生成树。
这个就显然可以进行凸优化了,二分斜率 (k) ,把白边权值 (+k) ,然后做最大生成树,看选出白边的数量与需求的关系就行了。
这样就得到了一个很好的 (O(nm log w ~alpha (n))) 的做法啦。(注意此处需要预处理排序,才能达到这个复杂度)
然后这样显然不够,我们继续考虑之前的权值是什么。白边的权值为 (mid + k - w_i) ,黑边的为 (w_i - mid) 。同时加上一个 (mid) 不会改变,那么就是 (2 imes mid + k - w_i) 和 (w_i) 。我们令 (C=2 imes mid + k) ,那么白边为 (C - w_i) ,黑边为 (w_i) 。
尝试一下二分 (C) ,然后直接判断呢?这样看起来很不真实,但却是对的。
这样可以保证在最大生成树上 (< mid) 与 (ge mid) 都各有一半。为什么呢?因为你考虑不存在,那么多的一边存在换到另外一边会更优的情况。
具体看官方解释:
首先对于 (M) 如果最大生成树 (T(M)) 含有黑边 (w_1-M) 和白边 (M-w_2) 且 (w_1<w_2) ,显然交换两条边为 (w_2-M,M-w_1) 更优(因为黑白边对应重合,交换总是可行的)。故所有黑边对应的 (w) 必然大于所有白边。那么如果最大生成树含有 (w< M) 的黑边或 (wge M) 的白边,必然只含一种,不妨设为黑边。那么设最小黑边原本的权值为 (w') ,取 (M'=w') ,可以发现其余边的权值之和不变,而这条黑边的权值从 (w'-M<0) 变成了 (0) ,增加了,故得到了一棵更大的生成树,所以这一定不是全局最大生成树。又由于方案数有限全局最大生成树(或者 (n-2) 条边生成森林)一定存在,其必然仅含有 (wge M) 的黑边和 (w<M) 的白边。
那么我们就除掉一个 (O(n)) 的复杂度啦。具体看代码实现qwq
(n) 为偶数其实也是没问题的,因为你总会选到中位数,不影响答案。
代码
#include <bits/stdc++.h>
#define For(i, l, r) for(register int i = (l), i##end = (int)(r); i <= i##end; ++i)
#define Fordown(i, r, l) for(register int i = (r), i##end = (int)(l); i >= i##end; --i)
#define Set(a, v) memset(a, v, sizeof(a))
#define Cpy(a, b) memcpy(a, b, sizeof(a))
#define debug(x) cout << #x << ": " << x << endl
#define DEBUG(...) fprintf(stderr, __VA_ARGS__)
using namespace std;
typedef long long ll;
inline bool chkmin(int &a, int b) {return b < a ? a = b, 1 : 0;}
inline bool chkmax(int &a, int b) {return b > a ? a = b, 1 : 0;}
inline int read() {
int x = 0, fh = 1; char ch = getchar();
for (; !isdigit(ch); ch = getchar()) if (ch == '-') fh = -1;
for (; isdigit(ch); ch = getchar()) x = (x << 1) + (x << 3) + (ch ^ 48);
return x * fh;
}
void File() {
#ifdef zjp_shadow
freopen ("566.in", "r", stdin);
freopen ("566.out", "w", stdout);
#endif
}
const int N = 2e5 + 1e3, M = 5e5 + 1e3;
int n, m;
namespace Union_Set {
int fa[N], Size[N];
void Init(int maxn) { For (i, 1, maxn) fa[i] = i, Size[i] = 0; }
int find(int x) { return x == fa[x] ? x : fa[x] = find(fa[x]); }
inline bool Union(int x, int y) {
int rtx = find(x), rty = find(y);
if (rtx == rty) return false;
if (Size[rtx] < Size[rty]) swap(rtx, rty);
Size[rtx] += Size[rty]; fa[rty] = rtx; return true;
}
}
struct Edge {
int u, v, w;
inline bool operator < (const Edge &rhs) const { return w > rhs.w; }
} lt[M];
ll ans, res; int use, need;
void Work(int lim) {
Union_Set :: Init(n); res = use = 0;
for (register int L = 1, R = m, cur = 0; L <= R; ) {
Edge add; register bool choose = false;
if (lt[L].w >= lim - lt[R].w) add = lt[L ++];
else add = lt[R --], choose = true, add.w = lim - add.w;
if (Union_Set :: Union(add.u, add.v)) {
res += add.w; if (choose) ++ use;
if (++ cur == need << 1) break;
}
}
res -= 1ll * lim * need;
}
int main () {
File();
n = read(); m = read(); need = (n - 1) >> 1; if (!need) return puts("0"), 0;
For (i, 1, m)
lt[i] = (Edge) {read(), read(), read()};
sort(lt + 1, lt + m + 1);
int l = 0, r = min(lt[1].w * 2 + 1, (int) 1e9);
while (l <= r) {
int mid = (l + r) >> 1; Work(mid);
if (use == need) return printf ("%lld
", res), 0;
if (use < need) l = mid + 1, ans = res; else r = mid - 1;
}
printf ("%lld
", ans);
return 0;
}