字典树 trie

Trie树

       Trie树，就是字母树。Trie树是多叉树，每个节点为一个字母。其根节点为象征节点（就是说没有含义，但是存在这个节点），从根节点开始建立，每个节点至多为26个子节点（不要我说为什么吧），这样，我们就可以用这种方便快捷的方式存储字符串。其应用也不言而喻，用于保存，统计，排序，查找大量字符串。因为很简单，我们不讲太多，根据图像，自己造几个字符串，慢慢理解，看看代码，一下就懂了。

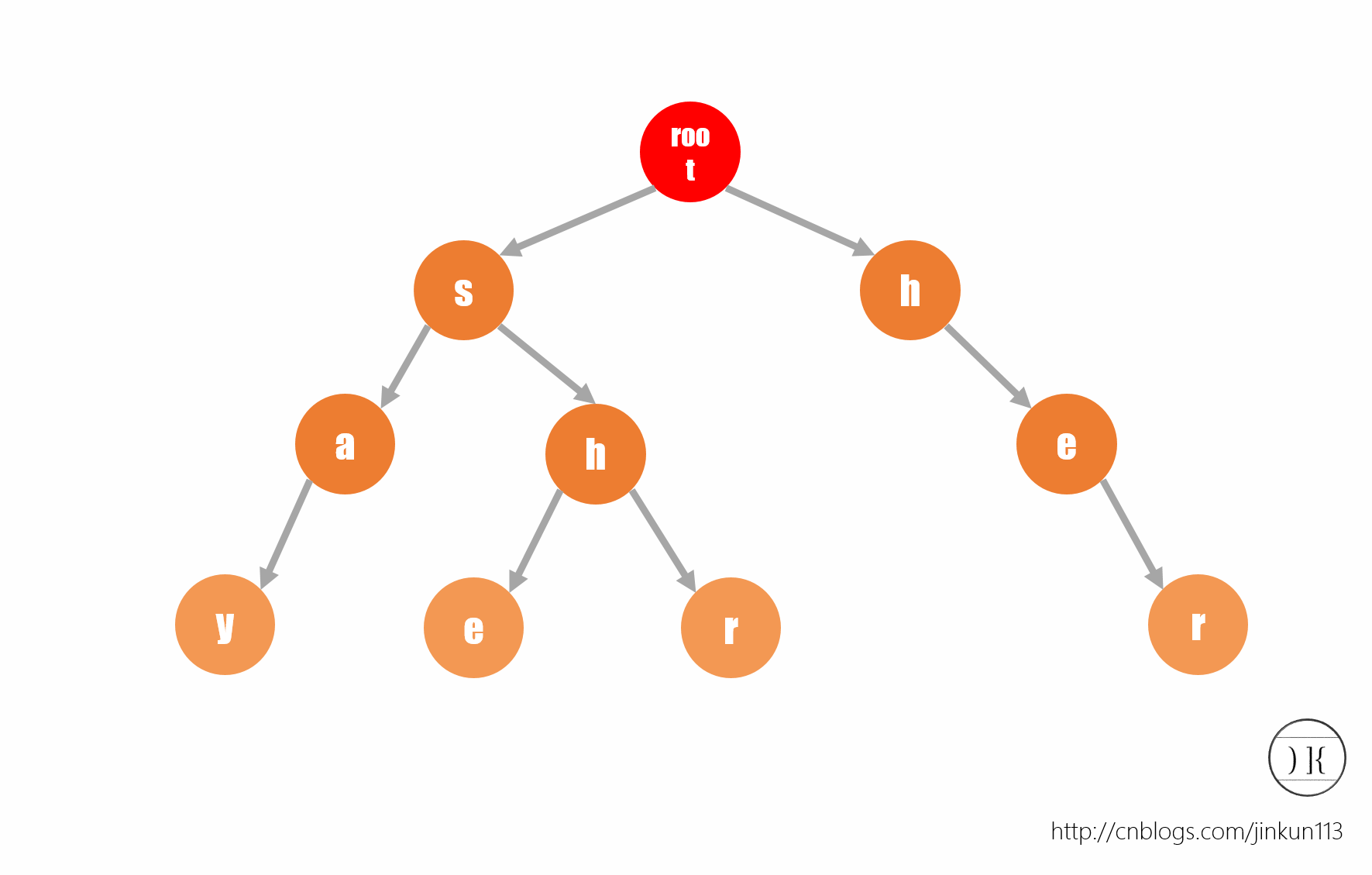
       如图所示，该字符串保存了say,she,shr,her四个字符串。有个小小的问题：在建树的时候，我们注意到最坏情况可能为二十六叉树，空间复杂度可想而知。所以，如果用指针可能更省空间。

 

 

 

Applications 应用

Trie (we pronounce "try") or prefix tree is a tree data structure, which is used for retrieval of a key in a dataset of strings. There are various applications of this very efficient data structure such as :

1. Autocomplete

Figure 1. Google Suggest in action.

2. Spell checker

Figure 2. A spell checker used in word processor.

3. IP routing (Longest prefix matching)

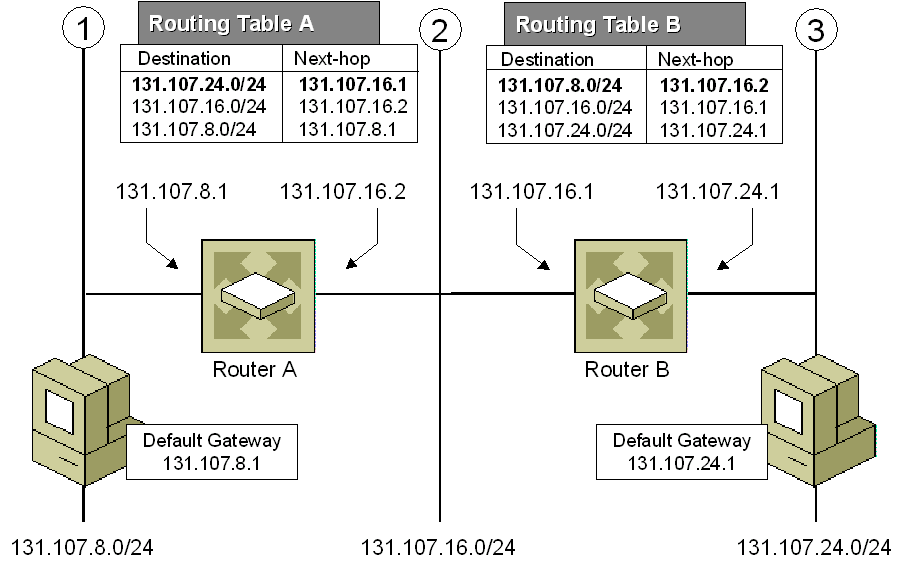
Figure 3. Longest prefix matching algorithm uses Tries in Internet Protocol (IP) routing to select an entry from a forwarding table.

4. T9 predictive text

Figure 4. T9 which stands for Text on 9 keys, was used on phones to input texts during the late 1990s.

5. Solving word games

Figure 5. Tries is used to solve Boggle efficiently by pruning the search space.

There are several other data structures, like balanced trees and hash tables, which give us the possibility to search for a word in a dataset of strings. Then why do we need trie? Although hash table has O(1)O(1) time complexity for looking for a key, it is not efficient in the following operations :

平衡树根hash表可以实现字符串搜索，为什么还需要trie?在以下操作时很低效

• Finding all keys with a common prefix.
• Enumerating a dataset of strings in lexicographical order.
• 寻找所有keys的共同前缀
• 以编辑顺序枚举所有的字符串

Another reason why trie outperforms hash table, is that as hash table increases in size, there are lots of hash collisions and the search time complexity could deteriorate to O(n)O(n), where nn is the number of keys inserted. Trie could use less space compared to Hash Table when storing many keys with the same prefix. In this case using trie has only O(m)O(m) time complexity, where mm is the key length. Searching for a key in a balanced tree costs O(m log n)O(mlogn) time complexity.

另一个原因，key变多之后，hash表会不断变大，导致冲突，时间复杂度会退化到O（n）.

Trie node structure

Trie is a rooted tree. Its nodes have the following fields:

• Maximum of RR links to its children, where each link corresponds to one of RR character values from dataset alphabet. In this article we assume that RR is 26, the number of lowercase latin letters.
• Boolean field which specifies whether the node corresponds to the end of the key, or is just a key prefix.

Figure 6. Representation of a key "leet" in trie.

Insertion of a key to a trie

We insert a key by searching into the trie. We start from the root and search a link, which corresponds to the first key character. There are two cases :

• A link exists. Then we move down the tree following the link to the next child level. The algorithm continues with searching for the next key character.
• A link does not exist. Then we create a new node and link it with the parent's link matching the current key character. We repeat this step until we encounter the last character of the key, then we mark the current node as an end node and the algorithm finishes.

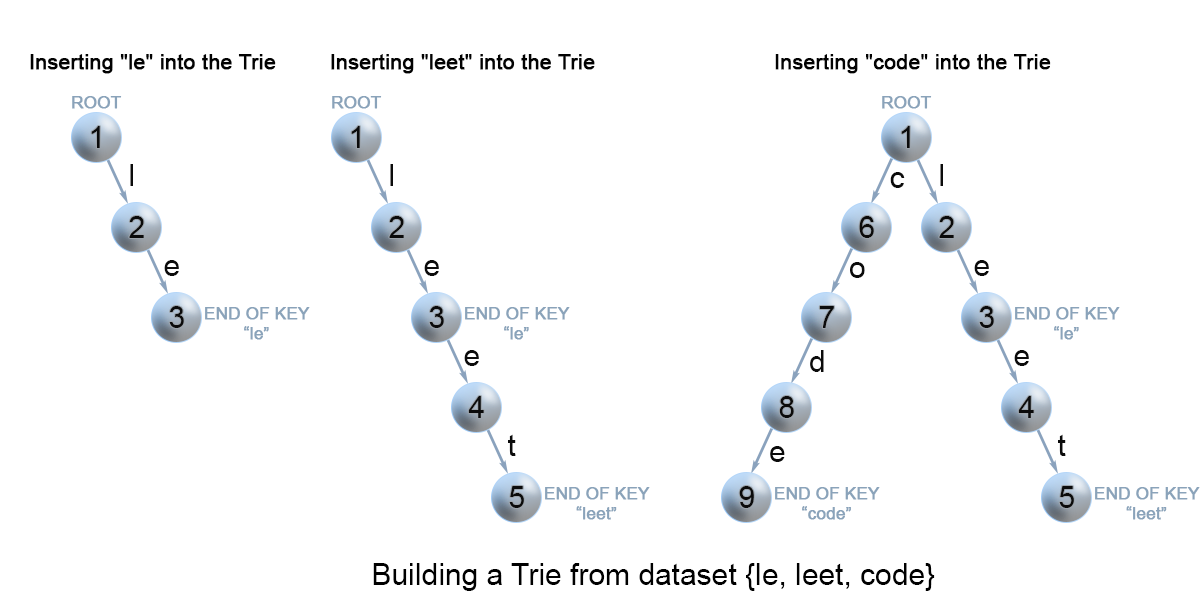
Figure 7. Insertion of keys into a trie.

 

Complexity Analysis

• Time complexity : O(m)O(m), where m is the key length.

In each iteration of the algorithm, we either examine or create a node in the trie till we reach the end of the key. This takes only mm operations.

• Space complexity : O(m)O(m).

In the worst case newly inserted key doesn't share a prefix with the the keys already inserted in the trie. We have to add mm new nodes, which takes us O(m)O(m) space.

Search for a key in a trie

Each key is represented in the trie as a path from the root to the internal node or leaf. We start from the root with the first key character. We examine the current node for a link corresponding to the key character. There are two cases :

• A link exist. We move to the next node in the path following this link, and proceed searching for the next key character.

• A link does not exist. If there are no available key characters and current node is marked as isEnd we return true. Otherwise there are possible two cases in each of them we return false :

  • There are key characters left, but it is impossible to follow the key path in the trie, and the key is missing.
  • No key characters left, but current node is not marked as isEnd. Therefore the search key is only a prefix of another key in the trie.

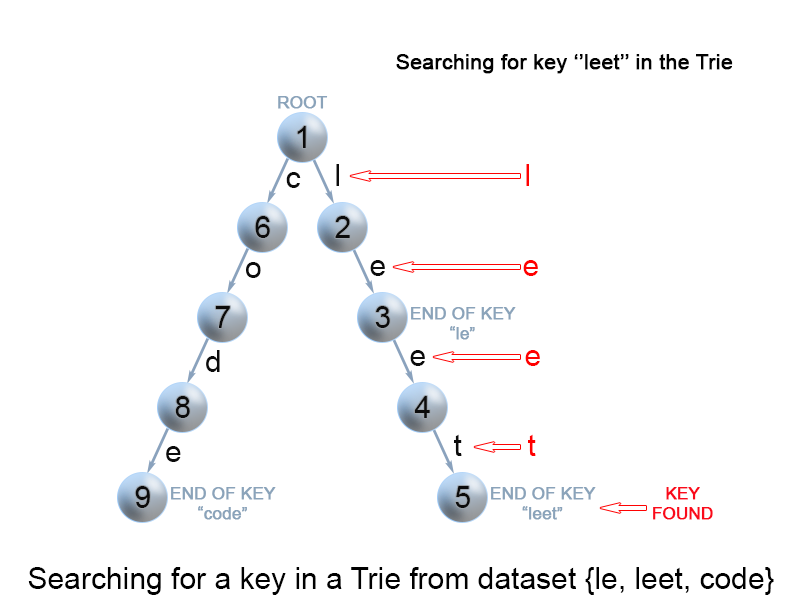
Figure 8. Search for a key in a trie.

 

Complexity Analysis

• Time complexity : O(m)O(m) In each step of the algorithm we search for the next key character. In the worst case the algorithm performs mm operations.

• Space complexity : O(1)O(1)

Search for a key prefix in a trie

The approach is very similar to the one we used for searching a key in a trie. We traverse the trie from the root, till there are no characters left in key prefix or it is impossible to continue the path in the trie with the current key character. The only difference with the mentioned above search for a key algorithm is that when we come to an end of the key prefix, we always return true. We don't need to consider the isEnd mark of the current trie node, because we are searching for a prefix of a key, not for a whole key.

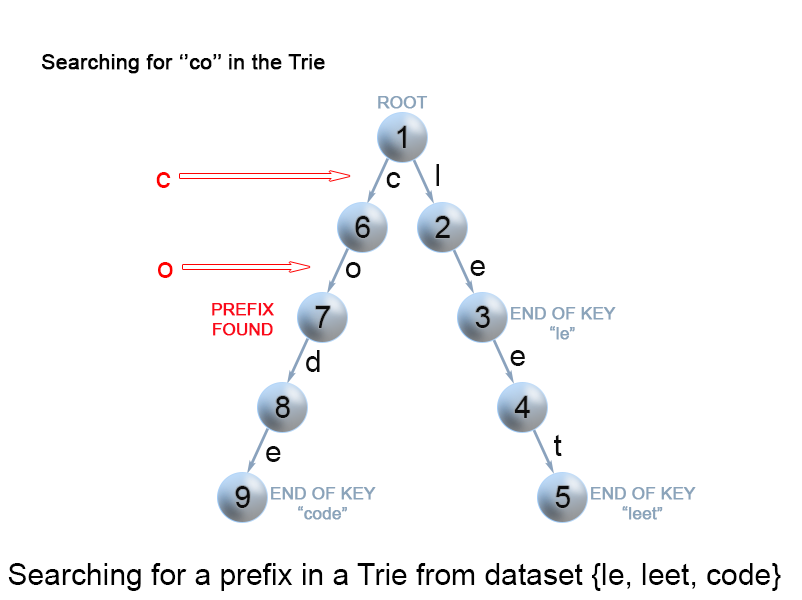
Figure 9. Search for a key prefix in a trie.

Complexity Analysis

• Time complexity : O(m)O(m)

• Space complexity : O(1)O(1)

Practice Problems

Here are some wonderful problems for you to practice which uses the Trie data structure.

1. Add and Search Word - Data structure design - Pretty much a direct application of Trie.
2. Word Search II - Similar to Boggle.

Analysis written by: @elmirap.