数论

取模运算

同余

设a,b是整数，若它们除以正整数m的余数相同，则称a,b对于模m同余，记为aΞb(mod m)。

费马小定理

假如p是质数，a是整数，且a、p互质，那么a的(p-1)次方除以p的余数恒等于1，即：a^(p-1)≡1(mod p)  可以改写为bb^c-2Ξ1(mod c)

但是反过来却不一定成立，就是说，如果a、p互质，且a^(p-1)≡1(mod p)，不能推出p是质数，比如Carmichael数。

加法和乘法形式相同

(a + b)%c = (a%c + b%c)%c

(ab)%c = (a%c)(b%c)%c

注意减法和除法的取模运算

(a − b)%c = (a%c − b%c + c)%c

(a / b)%c = ab^-1%c

最大公因数和最小公倍数

记a，b的最大公因数为gcd(a,b)

最大公因数的性质

1. gcd(a,b)=gcd(b,a)
2. gcd(a,b) = gcd(a − b,b)(a ≥ b)
3. gcd(a,b) = gcd(a%b,b)
4. gcd(a,b,c) = gcd(gcd(a,b),c)

性质2即为辗转相减法

性质3即为欧几里得算法

性质4可以说明多个数的最大公因数可以递推地进行求解

性质3求最大公因数的代码

int gcd(int a,int b)
{
    return b == 0 ? a : gcd(b,a%b);
}

最小公倍数lcm

int lcm(int a,int b)
{
    return a*b/gcd(a,b);
}

扩展欧几里得算法

考虑方程      ax+by=c      其中a,b,c是已知的正整数，如何求出方程的解

定理 上述方程有解的充要条件是 gcd(a,b)|c（c是 gcd(a,b)的倍数）

我们先将问题简化，求方程  ax+by=d 的解，其中 a,b是正整数， d=gcd(a,b)

算法过程

例 求方程   36x+28y=4  的解

1. 36=28×1+8
2. 28=8×3+4
3. 8=4×2
   

将前两步改写一下：

1. 8=36−28×1
2. 4=28−8×3
   

再代入一下，得
4=28−(36−28×1)×3=28×4+36×(−3)
因此

x=−3,y=4 是方程的一组解，方程的任一解可以表示成

  x=−3+7t
  y=4−9t

更一般地，方程 ax+by=d,d=gcd(a,b)的所有解为

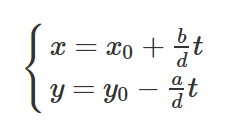    其中 x₀,y₀是一组特解

回到最开始的问题，方程 ax+by=c,gcd(a,b)|c的所有解为

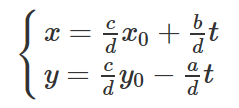其中 x₀,y₀是方程 ax+by=d,d=gcd(a,b)的一组特解.

ll ext_gcd(ll a,ll b,ll& x,ll& y)
{
    ll d = a;
    if (!b){
        x = 1;y = 0;
    }else{
        d = ext_gcd(b,a%b,y,x);
        y -= a/b*x;
    }
    return d;
}

回到前面除法取模中挖的坑，要找到 b^-1使得 bb^-1≡1(mod c)，实质上是求解方程 bx+cy=1中的 x，当然只有 gcd(b,c)=1时才有解，否则逆元不存在

素数

素数定义：如果一个数只能被1和它本身整除那么我们就成其为素数。

一般的素数判断

bool isPrime(int n)
{
    if(n==1)
    return false;
    for(int i=2;i*i<=n;i++)
        if(n%i==0)
        return false;
        return true;
}

素数筛

埃拉托斯特尼筛法，或者叫埃氏筛法

const int N = 100005;  
bool prime[N];  
void init()
{  
    for(int i=2;i<N;i++) 
    prime[i]=true;//先全部初始化为素数  
        for(int i=2;i<N;i++)
        {  
            if(prime[i])//如果i是素数
            {  
                 for(int j=i*i;j<N;j+=i)//从i的两倍开始的所有的倍数(i*i也行)
                 {  
                       prime[j] = false;  
                 }  
            }  
        }  
}

这种方法的原理是从小到大将素数的倍数筛掉，复杂度为 O(n*logn)，注意到每个合数如果有多个素因子，那么就 会被重复筛掉，造成复杂度的浪费，因此，用下面的方法可以保证每个合数只被它最小的素因子筛掉一遍，以O(n)的复杂度解决上述问题

线性筛法（欧拉筛）

ll getPrime(ll n,bool vis[],ll prime[]){
    ll tot=0;
    for(ll i=1;i<=n;i++)vis[i]=0;
    for(ll i=2;i<=n;i++){
        if(!vis[i])prime[tot++]=i;
        for(ll j=0;j<tot;j++){
            if(prime[j]*i>n)break;
            vis[prime[j]*i]=1;
            if(i%prime[j]==0)break;
        }
    }
    return tot;
}

 Miller_Rabin大素数判定

  bool miller_rabin(long long n)//Miller-Rabin素数检测算法  
  {      
      long long i,j,a,x,y,t,u,s=10;      
      if(n==2)        
        return true;      
      if(n<2||!(n&1))        
        return false;      
      for(t=0,u=n-1;!(u&1);t++,u>>=1);//n-1=u*2^t      
      for(i=0;i<s;i++)      
      {          
         a=rand()%(n-1)+1;          
         x=ModExp(a,u,n);          
         for(j=0;j<t;j++)          
         {              
             y=mood(x,x,n); //对x的x次方快速幂然后对n取模             
             if(y==1&&x!=1&&x!=n-1)                
             return false;              
             x=y;          
         }          
         if(x!=1)            
         return false;     
      }      
         return true;
   }
            

 预处理每个数的所有质因数

const int N = 100000 + 5;  
vector<int > prime_factor[N];  
void init()
{  
    for(int i = 2; i < N; i ++)
        if(prime_factor[i].size() == 0)//如果i是质数
            for(int j = i; j < N; j += i)
                prime_factor[j].push_back(i);   
}

预处理每个数的所有因数

const int N = 100000 + 5;  
vector<int > factor[N];  
void init()
{  
    for(int i = 2; i < N; i ++)
        for(int j = i; j < N; j += i)
            factor[j].push_back(i);
}

预处理每个数的质因数分解

const int N = 100000 + 5;  
vector<int > prime_factor[N];  
void init()
{  
    int temp;  
    for(int i = 2; i < N; i ++)
        {  
        if(prime_factor[i].size() == 0)
        {  
            for(int j = i; j < N; j += i)
            {  
                temp = j;  
                while(temp % i == 0)
                {  
                    prime_factor[j].push_back(i);  
                    temp /= i;  
                }  
            }  
        }  
    }  
}

组合数运算和快速幂见另一篇博客https://www.cnblogs.com/zlhdbk/p/10548959.html