codeforces 903D

D. Almost Difference

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Let's denote a function

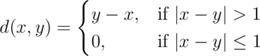
You are given an array a consisting of n integers. You have to calculate the sum of d(ai, aj) over all pairs (i, j) such that 1 ≤ i ≤ j ≤ n.

Input

The first line contains one integer n (1 ≤ n ≤ 200000) — the number of elements in a.

The second line contains n integers a1, a2, ..., an (1 ≤ ai ≤ 109) — elements of the array.

Output

Print one integer — the sum of d(ai, aj) over all pairs (i, j) such that 1 ≤ i ≤ j ≤ n.

Examples

input

5
1 2 3 1 3

output

4

input

4
6 6 5 5

output

0

input

4
6 6 4 4

output

-8

Note

In the first example:

1. d(a1, a2) = 0;
2. d(a1, a3) = 2;
3. d(a1, a4) = 0;
4. d(a1, a5) = 2;
5. d(a2, a3) = 0;
6. d(a2, a4) = 0;
7. d(a2, a5) = 0;
8. d(a3, a4) =  - 2;
9. d(a3, a5) = 0;
10. d(a4, a5) = 2.

题意很好理解，这里就不说了。

解题思路：由给出的公式可以得到d(a1,an)+d(a2,an)+d(a3,an)+...+d(ai,an)的答案是i*an-sum (sum是a1~ai中与an差的绝对值大于1的数之和，那么这样只需要遍历一遍数组，执行i*an-sum并减去a1~ai中与an差的绝对值小于等于1的数就行了。所以还要用map记录一下。

坑点：注意数据1e9,1e9-2,1e9-4...-1e9+4,-1e9+2,-1e9 (共有200000个 ，这种时候答案近似于100000*100000*1e9 数据会爆long long,所以要用long double

附ac代码：

#include <cstdio>
#include <cstring>
#include <string>
#include <iostream>
#include <algorithm>
#include <map>
#include <iomanip>
using namespace std;
typedef long double ld;
const int maxn = 200000+10;
ld nu[maxn];
map<ld,ld>mp;
int main()
{
    int n;
    scanf("%d",&n);
    for(int i=0;i<n;++i)
        cin>>nu[i];
    ld s=0;
    ld sum=0;
    mp.clear();
    for(int i=0;i<n;++i) //根据推出的公式可得，i从0开始比较简单
    {
        s+=i*nu[i]-sum+mp[nu[i]+1]-mp[nu[i]-1];
        //s+=((i-mp[nu[i]-1]-mp[nu[i]+1]-mp[nu[i]])*nu[i]-(sum-mp[nu[i]+1]*(nu[i]+1)-mp[nu[i]-1]*(nu[i]-1)-mp[nu[i]]*[i]));
        mp[nu[i]]++;
        sum+=nu[i];
    }
    cout<<fixed<<setprecision(0)<<s<<endl;
    return 0;
}