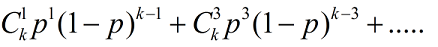【非原创】LightOJ

学习博客：

戳这里

戳这里 　　

戳这里

戳这里

题意：
在一个三维的空间，每个点都有一盏灯，开始全是关的,
现在每次随机选两个点，把两个点之间的全部点，开关都按一遍；问ｋ次过后开着的灯的期望数量；

题解：

肯定不能从随机抽取两个数这里入手的，要求开着的灯的数量就从对每一盏灯，操作结束后灯开着的概率，然后将这些概率求和就是对于整个矩阵到最后开着的灯的数量了，这就把矩阵的问题落实到了对于求每个坐标的概率的问题。

对每个点单独计算贡献，即k次过后每个点开关被按了奇数次的期望

一个点如果被包到所选空间里，那么说明选的两个点，x坐标在这个点两侧，y坐标在这个点两侧，z坐标在这个点两侧；

对于一维的，可以用求出两个点在x这一点两侧的概率。然后三维的只要当成三个一维的乘起来就行了。

E=

求法：

 代码（亦非原创）：

#include<bits/stdc++.h>

using namespace std;

int t,x,y,z,m;

int main()

{

    scanf("%d",&t);

    int cas=0;

    while(t--)

    {

        scanf("%d%d%d%d",&x,&y,&z,&m);

        double ans=0.0;

        for(int i=1;i<=x;i++)

        for(int j=1;j<=y;j++)

        for(int k=1;k<=z;k++)

        {

            double p=0.0;

            p= 1.0-1.0*((x-i)*(x-i)+(i-1)*(i-1))/(x*x);

            p*=1.0-1.0*((y-j)*(y-j)+(j-1)*(j-1))/(y*y);

            p*=1.0-1.0*((z-k)*(z-k)+(k-1)*(k-1))/(z*z);

 

            ans+=0.5-0.5*pow(1.0-2*p,1.0*m);

        }

        printf("Case %d: %.11lf
",++cas,ans);

    }

    return 0;

}