在straight模型中,F0被看成是瞬时频率,从1999年straight模型被提出,到目前的TANDEM-STRAIGHT等各个版本中,先后有4种语音信号基频提取方法, 1)基于AM-FM,利用滤波器使判别值最大(1999a);2)fixed-point法(1999b);3)YIN auto-correlation法(02、05);4)spectral division法(08,for TANDEM)。这里准备对第2、4种方法加以研究。
1基于fixed-point的基频提取法
该方法是99年提出的,详见论文《Fixed Point Analysis of Frequency to Instantaneous Frequency Mapping for Accurate Estimation of F0 and Periodicity》。
1.1基本思路
该方法实际上是利用Hilbert变换,得到正交信号,从而得到瞬时频率,作为基频,这后面还会再讲。不过在那之前,首先需对信号滤波,比如我们先验地知道,语音的基频在60~500Hz的范围内,则可以将这段频率,在log域(适应人耳)内平均划分为若干份(如104份),设计若干滤波器,分别滤出相应频段的信号,再对信号进行瞬时频率提取。
那么首先滤波器的设计是一个重点。为简单起见,采用FIR滤波器,冲激相应就是滤波器系数(卷积系数),且具有线性相位,这在上一篇报告中详细讲了。先设计LP滤波器,再变频为BP滤波器。为了获得好的频率响应,采用类似Gabor变换的方法,设计滤波器系数(FIR中即冲激响应)为
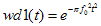
其中f0为所设计的中心频率,其傅里叶变化仍为类高斯函数,带宽约为2f0。为了进一步压缩带宽,用另一B-锤形函数与它卷积
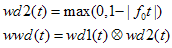
从而可以进一步压缩带宽为f0。要变为BP滤波器,只要乘以余弦即可变频

由下面两个例子可以更形象的看出这种滤波器的设计思路。
T0=10.5ms,f0=95.2Hz时
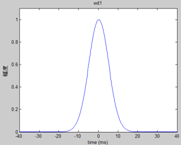
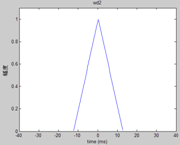
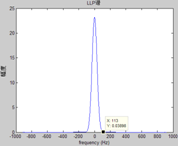

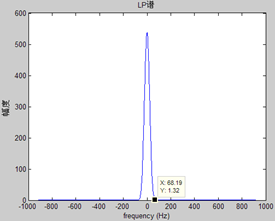
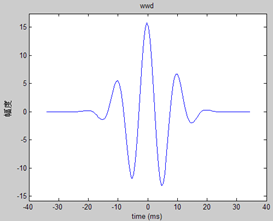
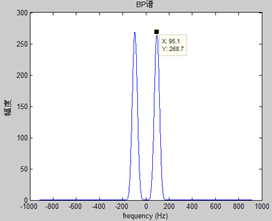
T0=7.87ms,f0=127.1Hz时
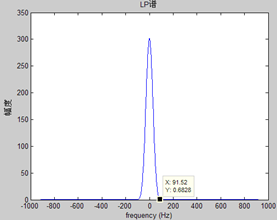

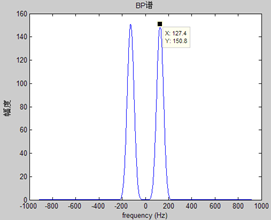
提取瞬时频率,一个常用的方法是利用正交信号。举最简单的例子
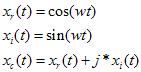
xr(t)和xi(t)是一对正交信号,由他们构成复解析信号xc(t),那么提取xc(t)的瞬时相位,再对时间微分即可获得角频率
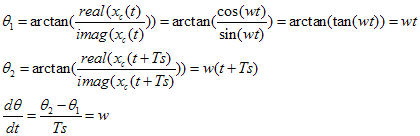
这种关系,对于非单纯余弦信号同样适用,因此这也成为提取瞬时频率的一种常用方法。那关键就是如何获取一个信号的正交信号,这其实就是著名的Hilbert变换。它是时间域到时间域的变换,也可以看成一个滤波器,其频率响应如下,滤得的信号与原信号正交,可以用cos,sin函数做一个验证。
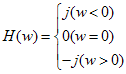
教科书中常用的表达方式为
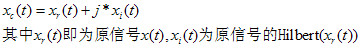
在我们的应用场景中,可用一个巧妙的方法获得xc(t),具体如下
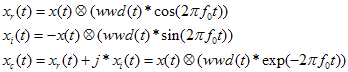
那关键就是这里的xr(t)和xi(t)是否是正交的,我们可以从它们的频谱中判断
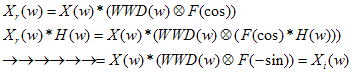
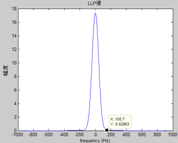
到此,基本的原理就清楚了,如下图,是用第30个滤波器(即f0=95.2Hz)滤得的信号,经上述方法,得到的瞬时频率的轨迹图,可以看出总体上在130Hz附近,还是比较准确的。
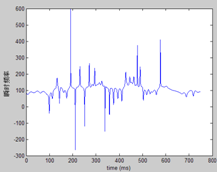
1.2基频提取方法
在某一时刻,每个滤波器滤得的信号都会有一个瞬时频率,如下图蓝色线所示,横坐标表示滤波器的中心频率,纵坐标表示该滤波器所得信号此刻的瞬时频率。图中红线表示滤波器的中心频率。
显然,若信号的瞬时频率为f0,则附近的几个滤波器滤得的信号,在此刻的瞬时频率都应该是f0,即在该频率段应该近似为水平,与红线的交点即是该处的瞬时频率,如左图所示。所有这些点都称为fixed-point,而其中最平的那个应该是基音频率,另两个应该是二次、三次谐波。


如上图右所示,是10ms处的,此处为unvoiced段,貌似也有fixed-point,但我们知道那不是,因为这里都是噪声,没有基音。STRAIGHT采用一种叫carrier-to-noise-ratio(C/N比)的参数来判别所得的fixed-point是否为基音频率。
信号经某一滤波器滤波后,得到中心为wc(即fixed-point指示的频率)的信号,那现在我们要确定该频率点是否为元音部分基音频率,还是清音部分的类噪声频率。首先我们假设滤波后的信号,由频率为wc的主要部分,和频率在wc附近的次要部分组成,如下
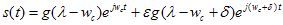
其中g()为滤波器的频率响应(归一化的),g(0)附近近似为1;δ为次要部分的频偏,ε为次要部分的幅度值(以主要部分归一为参考)。那么我们的任务就是求出ε的值,若它足够小,则说明主要部分是突出的,即可认为主要部分就是基音成分;否则,若ε值较大,和1相仿,则表明主要成分和次要成分一样,都是噪声。
怎么求ε呢?时域信号混在一起,分不开主次部分,只能从频域入手,对上式近似得
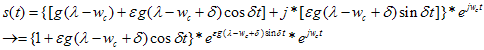
这步近似是认为实部约为1,虚部很小,所以写成指数形式,角度就为虚部。然后可以得
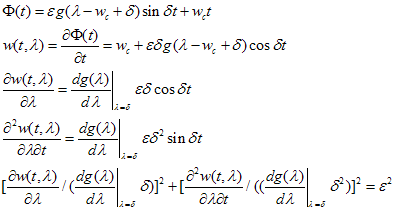
其中w(t,f)我们是知道的,每个滤波器滤得的信号的瞬时频率轨迹构成t的函数,所有滤波器又构成f的函数;另外滤波器的频响g我们也是直到的;关于频偏δ,我们可以取wc附近的若干值,然后求平均。
这样就得到了所谓的C/N比,如下图所示

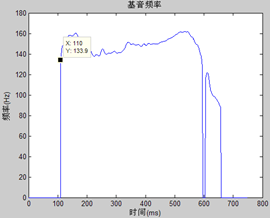
收索的过程还需要一些软件技巧,C/N值cnr并不能绝对地来判定,我们为它设定两个阈值,hth=0.12,lth=0.9,低于hth,则认为一定是元音部分,高于lth,则认为一定是非元音部分,介于中间的则需另作判定。判定的方法是利用基因频率的连续性,即一个元音段内,基频是连续变化的,不应出现陡然变化,我们设为thf0j=(f(n+1)-f(n))/f(n),设定阈值为4%。另外设一变量von指示上个时间点是否为元音段,为1表是,为0表不是。
软件流程如下:
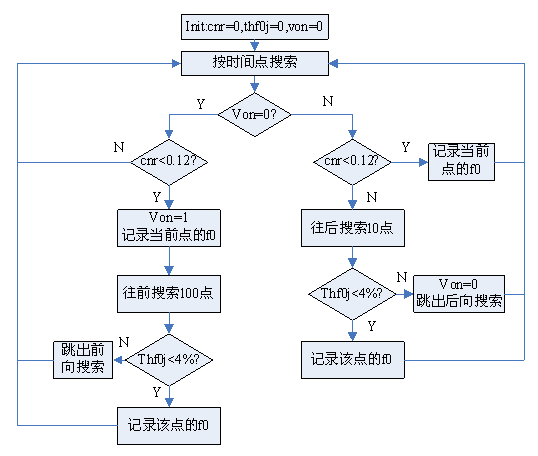
2.基频自适应频谱分析
STRAIGHT模型一个重要的部分就是自适应频谱分析,即要得到平滑的、无干扰的谱。那么到底有什么干扰呢?源于何?怎么消除?后面再看。做谱分析,首先要选窗函数,下面先看两个例子。
设一信号,基频为100Hz,共有5次谐波,幅度都相同,采样频率为1000Hz,分别用两种窗,得到的频谱如下图所示:
wRect 不同时刻
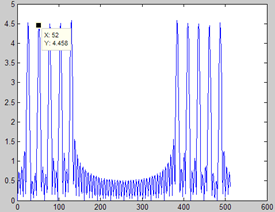
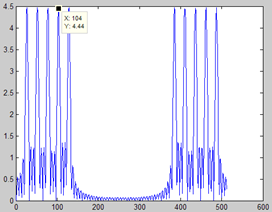
wGaussian 不同时刻

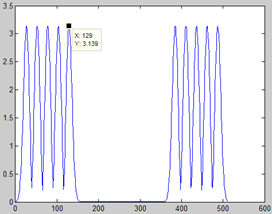
矩形窗主瓣较窄,频率分辨率,但旁瓣较大;高斯窗的时域、频域都是高斯函数,主瓣较宽,频率分辨率不高,但没有旁瓣,且其时域和频域的分辨率相同(分别相对于t0、f0),是时频分析的基础,相关的知识还需查阅资料。
要得到平滑的频谱,一般采用高斯窗。不过首先要注意的是,不管用什么窗,所得的频谱都会在时域上有周期波动,尤其是谷值处,这是相位的影响。再看频域,首先给出高斯窗函数
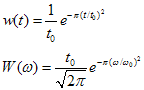
设计高斯窗首先需估计出基频的周期,如上图所示,都是在得知准确的基频周期后,所得的频谱,幅度很准确。但若基音估计不准呢,如下图左,是fes=2f0时的频谱。这称为频域上的周期波动。STRAIGHT把它们统称为time-frequency periodicity interferences,也是它要消除的(eliminate)。
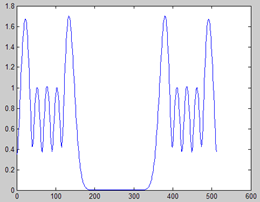
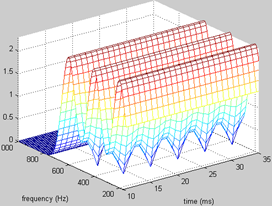
实际中,我发现,只要基频估计得不是太离谱,所得频谱的频域波动并不会很大,不会像上图那样夸张,但是它带来了频谱时域上的波动却是很明显的。另外,当fs很高时,fft后每点代表频率值很大,即频率的分辨率较低,由于窗泄露的问题,得到的频谱也不准确。下面两张图分别是基音估计准确与有10%误差时,所得到的spectrogram三维图:
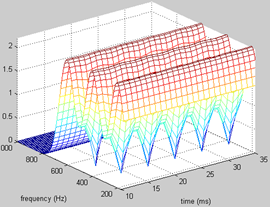
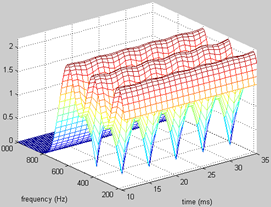
可见,基频估计误差在频率轴上引起的波动不是很大,但在时间轴上引起的波动却很明显,另外,频谱谷值处的时域上周期性地存在空洞hole,这是由于不同时刻的信号的相位差异造成的。要消除这两种波动,采取了两种办法。
消除基频估计误差带来的波动,是利用改进窗的方法,使原高斯窗与一个锤形窗卷积
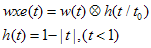
这样得到的窗谱主瓣更窄,也确实消除了时域上的波动,如下图左,为什么??
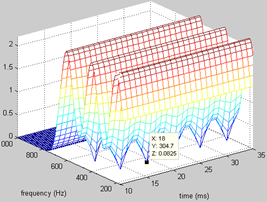
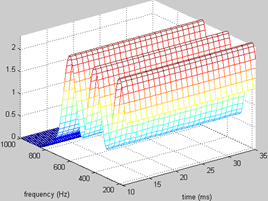
消除谷值处的空洞hole,是利用了互补的方法,即再用另一个窗,然后把两窗得到的频谱相加。如上图右所示,所用系数0.28^2。

两窗wxe、wxd只是从低通变为带通的频谱搬移,且搬移的距离为0.5f0(即那个sin函数的频率)。另外我们知道所得谱是实际谱与窗函数谱的卷积,我们用的窗函数谱的带宽约为f0(前面有验证),即中间为峰值,两边0.5f0处为谷值。
PC的谱是由Po的谱分别向两边移0.5f0在相加的结果,与Po的谷峰值刚好相反,因此相加则可平衡。其得到的谱如下图所示:

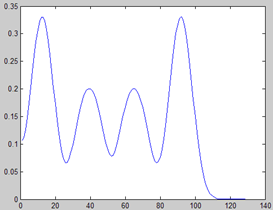

这些基本弄懂了,觉得还是有问题,主要3个:1)高斯窗和锤形窗卷积后,只是使得该窗的主瓣更窄了些,因此它起得作用主要是抑制各谐波间的干扰,达到了一定的消除波动的效果。但频谱在频域内的波动主要是fs较高时,频域分辨率低,由窗函数泄露引起的误差,该方法没有考虑这个吧(还是我没理解??)!如下图,是将fs提高5倍后所得谱

2)消除空洞hole时,用了两个互补窗叠加的方法,这多少有点像凑的,没什么理论意义(还是我不理解??),且系数选择不太稳定,即用论文中的0.136,对有些频谱好像不对,比如该文中用了0.28^2较准确。
3)空洞(即时域波动)由不同时刻信号的相位引起(联想周期延拓的概念),那么消除了它,将相当于舍弃了相位信息啊?合成时应由补偿。另外到底怎么消除才好呢,是填补空洞,还是移除突起内??这也不好说吧。应该是填补,最终要得到谱包络。
3.语音合成及参数控制原理
前面得到了基频轨迹、基频自适应的频谱。还是用例子来说明,设信号基频100Hz,共有15次谐波,其幅度成阶梯状,采样频率为10000Hz。首先来看其频谱,如下图分别是直接SFT分析及基频自适应+互补法所得的频谱,(前两张是不同时刻的SFT谱,细看还是有差异的,但论文中方法所得谱都差不多,如第三张),可见利用上述的方法确实显著改善了频谱形状。但也有问题,如实际的高低幅度比为2:1,直接SFT谱中还勉强吻合,然而后者中比为5:3.2左右。
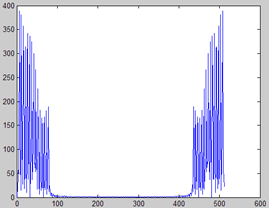

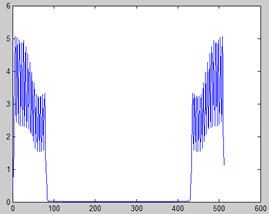
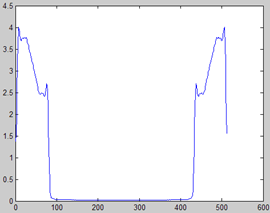
这里的频谱是取的abs()幅度,再有前面的互补法可得知这种谱是完全省略了相位信息,那么它得到的波形是怎样呢?另外更重要的一点是,我们一直说,提取基频轨迹,并自适应分析频谱,目的就是要是语音分解为基频和谱相独立的部分,好分别控制,然而,我们得到的谱还是有基频信息的(并没完全分离),其中一条条谱线正是谐波分量啊。因此我们想到谱包络,那样就展现了频谱的整体状况,而和具体的频率分开了,可采用卷积的方法,详见getF0AdaptiveSpectral()的最后几行代码,包络如上图。
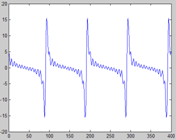
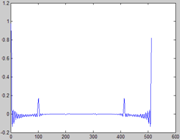
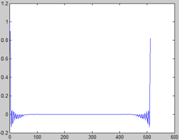
如上图,分别是原信号,自适应谱的信号,谱包络的信号。由于自适应谱的空洞被填补,已倾向于包络。包络则是完全撇开了基频的影响,那么给定新的基频,怎么合成出信号呢?这里其实是利用了一个基本原理,新信号的频谱应该是谱包络被一串脉冲抽样(以新基频为周期),那到时域了,就是信号的周期延拓(以基频周期为周期)。
好!我们现在用新基频200Hz来合成新信号(谱包络信号先进行一个fftshift移位)。得到的新信号及其频谱如下图所示。可以看出,新信号的频谱仍保持原谱的包络特征,只是基频变了。
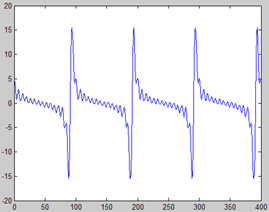
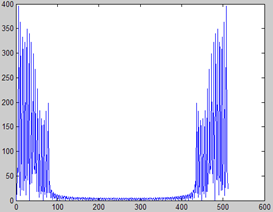

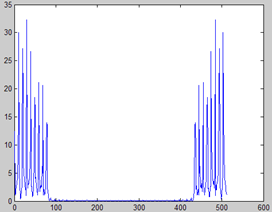
但也很明显看出其差距,原信号幅度是正负对称的,而新信号却几乎为正。这主要是因为相位信息的丢失,谱包络是实数,其相频响应恒为零,我们可以人为地给它加上相位,先通过幅频响应得到唯一的最小相位谱,在此基础上,在用一个随机相位的全通滤波器,为该最小相位再加上一些随机相位。
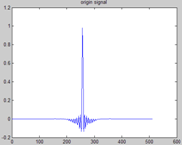
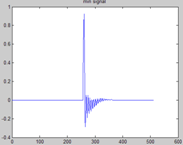

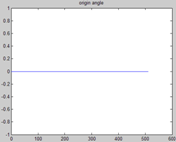
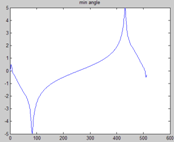
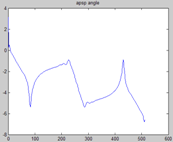
上图分别是原谱、最小相位谱、随机相位全通谱所得的信号波形及其相频响应,从中可以看出它们所反映的事情,至于最小相位系统、全通系统的原理及实现,以后再看吧。注意一下,原谱的相位为0,其实是线性相位,联想FIR滤波器,w从0到2pi,相位变化很大的,为2k*pi。