0.PTA得分截图

1.本周学习总结
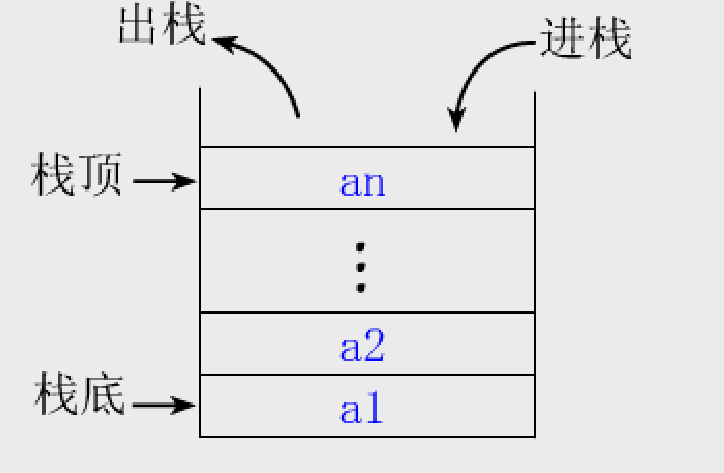
1.1 栈的基本操作内容
1.1.1栈的定义及其特点
- 栈是一种只能在其一端进行插入或删除操作的线性表。允许插入和删除的一端称为栈顶,不允许的另一端则称为栈底。
- 栈的特点是:先进后出、时进时出(即栈未满也可出栈)。
- 栈的存储结构:顺序栈和链栈
顺序栈:
1.1.2栈结构定义
顺序栈:

- 顺序栈实际就是利用数组来存储数据。而栈顶指针top,则用来表示当前栈顶元素的数组下标,因此定义为int。
链栈:
采用链表存储的栈称为链栈,采用带头结点的单链表实现。

1.1.3初始化栈
顺序栈
void InitStack(SqStack& s)
{
s = new Stack;
s->top = -1;
}
链栈
void InitStack(LiStack& s)
{
s = new LiNode;
s->next = NULL;
}
- 初始化链表时,与新建链表操作相同,初始时即指向空。
对比pta 6-1另类堆栈(顺序栈) 中不同定义形式的初始化写法
结构定义:
struct SNode {
ElementType *Data; /* 存储元素的数组 */
Position Top; /* 栈顶指针 */
int MaxSize; /* 堆栈最大容量 */
};
typedef PtrToSNode Stack;
初始化函数:
Stack CreateStack( int MaxSize )
{
Stack S = (Stack)malloc(sizeof(struct SNode));
S->Data = (ElementType *)malloc(MaxSize * sizeof(ElementType));
S->Top = 0;
S->MaxSize = MaxSize;
return S;
}
- 注意此时S申请内存时如何用/* C语言 */写。
- 此时题意是Top定义为栈顶的上一个位置。因此初始化 S->Top = 0;
- 注意此时定义的结构中/* S->data是指针 */,因此同样/* 需要为其申请数组大小的内存 */。指针类型为ElementType *,数组大小为MaxSize,数组中要存储的数据类型为:ElementType,因此申请大小为MaxSize * sizeof(ElementType)。
1.1.4销毁栈
顺序栈:
void DestroyStack(SqStack& s)
{
delete s;
}
- 注意此时的顺序栈我们可以直接delete s;
链栈:
void DestroyStack(LiStack& s)
{
LiStack p;
while (s != NULL)
{
p = s;
s = s->next;
free(p);
}
}
- 注意与顺序栈销毁操作不同,链栈中的每个结点都需释放。
1.1.5判断栈是否为空
顺序栈:
bool StackEmpty(SqStack s)
{
return(s->top == -1);
}
链栈:
bool StackEmpty(LiStack s)
{
return(s->next == NULL);
}
1.1.6进栈
顺序栈:
bool Push(SqStack& s, ElemType e)
{
if (s->top == MaxSize - 1)
return false;
s->top++; //栈顶指针增1
s->data[s->top] = e;
return true;
}
- 注意进栈操作我们要先判断是否栈满,否则就会溢出。因为我们使用的是顺序栈,有数组长度MaxSize限制。
- 根据特性将栈顶指针先移动到新位置,再给新的栈顶位置赋值,即为进栈。
链栈:
void Push(LiStack& s, ElemType e)
{
LiStack p;
p = new LiNode;
p->data = e; //新建元素e对应的节点*p
p->next = s->next; //插入*p节点作为开始节点
s->next = p;
}
-
由于链表的特点,链栈我们则无需考虑链栈满的情况
-
依据栈的先进后出的特点,我们采用头插法插入链中
1.1.7出栈
顺序栈:
bool Pop(SqStack& s, ElemType& e)
{
if (s->top == -1) //栈为空的情况,栈下溢出
return false;
e = s->data[s->top];//取栈顶指针元素
s->top--; //栈顶指针减1
return true;
}
-
注意该函数头的写法:* ElemType& e *。在该出栈过程中,我们是先取栈顶元素值赋给e,再移动指针。所以该出栈操作中,我们不仅出栈,还记录了出栈元素e。
-
需注意的是,此时我们仅仅是将记录了出栈元素的值,然后指针移动,实现逻辑上的出栈删除,但实际上该元素并未删除。即此时s->data[s->top+1]==e**
链栈
bool Pop(LiStack& s, ElemType& e)
{
LiStack p;
if (s->next == NULL) //栈空的情况
return false;
p = s->next; //p指向开始节点
e = p->data;
s->next = p->next; //删除*p节点
free(p); //释放*p节点
return true;
}
-
出链栈操作实际上 相当于 链表删除链头元素(头结点后的第一个元素)。
-
注意出链栈过程中有:free(p);因此是真实地删除了该结点。
1.1.8取栈顶元素
顺序栈:
bool GetTop(SqStack* s, ElemType& e)
{
if (s->top == -1) //先判断栈为空的情况
return false;
e = s->data[s->top];
return true;
}
- 与出栈相同,取元素先判断是否栈空
链栈:
bool GetTop(LiStack s, ElemType& e)
{
if (s->next == NULL) //栈空的情况
return false;
e = s->next->data;
return true;
}
1.1.9共享栈
-
即两个相同类型的栈共享同一个数组。

-
两栈分别以数组头和尾为栈顶,不断储存元素向中间靠拢。
-
共享栈的重要操作
共享栈的结构定义:
typedef struct
{
ElemType data[MaxSize];
int top1,top2; //两个栈的栈顶指针
} Stack;
/*共享中栈的重要判断条件*/
- 判断栈1空条件:top1 == -1
- 判断栈2空条件: top2 == MaxSize
- 判断栈满条件: top1 + 1 = top2
1.2队列的基本操作及内容
1.2.1队列的定义及其特点
- 队列:只允许在表的一端进行插入,而在表的另一端进行删除的线性表。
- 队尾(rear)——允许插入的一端,队头(front)——允许删除的一端
- 队列特点:先进先出(FIFO)
- 队的存储方式:顺序队和链队。
顺序队:

1.2.2队列的结构定义
顺序队
typedf struct
{
Elemtype data[MaxSize];
int front;//队头指针;
int rear;//队尾指针;
}Queue;
链队
typedef struct node//用于保存每个结点;
{
Elemtype data;
struct node *next;
}Node,*LinkNode;
typedef struct
{
LinkNode front;//队头指针;
LinkNode rear;//队尾指针;
}Queue;
- 注意链队的结构定义,链队的结点和链队的首尾指针分开定义
1.2.3初始化队列
顺序队
void InitQueue(Queue &q)
{
q = new Queue;
q.front=q.rear=-1;
}
链队
void InitQueue(Queue &q)
{
q = new Queue;
q.front->next = q.rear->next = NULL;
}
-
注意我们构造的链队通常是带头结点,实际上队头位置就相当于链头结点位置
-
注意此时指向写法。如q.front->next = NULL。front是q的结构体成员所以用‘.’,而q.front则是指针,类型为LinkNode,所以用“->”指向。
1.2.4判断是否队空
顺序队和链队一样
bool IsEmpty(Queue &q)
{
if(q.rear==q.front) return true; //队空
else return false; //队不空
}
1.2.5进队
顺序队
bool Push(Queue& q, Elemtype e)
{
if (q.rear == MaxSize - 1) return false;//在进队之前一定要先判断是否队满;
else
{
q.rear++; q.data[q.rear] = e;
return true;
}
}
链队
void Push(Queue& q, Elemtype e)
{
LinkNode p;
p->data = e;
p->next = NULL;
q.rear->next = qtr;//尾插入队
q.rear = qtr;
}
- 同样的链队也无需考虑链队满的情况
- 此时链队即是用尾插法入队
- 注意初始化时我们令 q.front->next = q.rear->next,即空链队时首尾指向同处,因此无需另做处理(链队空时将队头指向p)。
1.2.6出队
顺序队
bool Pop(Queue& q, Elemtype& e)
{
if (q.rear==q.front) return false;//出栈是要先判断是否为空栈
else
{
q.front++;
e = q.data[q.front];
return true;
}
}
- 注意与栈的操作不同,由于队头指针指向的是队头元素的前一个位置,因此是先增加下标再取元素值。
- 同样的队头加一,只是下标变了,并未真正删除。
链队
bool Pop(Queue& q, Elentype& e)
{
LinkNode p;
if (q.rear == q.front) return false;//若队已空
else
{
p = q.front->next;//用p保存要出队的结点;
q.front->next = p->next;
e = p->data;
delete p;//删除结点;
}
}
- 此时相当是链中删除头结点后的结点。
- 注意delete p;说明链队是真正的删除了该元素
1.2.7销毁队列
顺序队
void DestroyQueue(Queue &q)
{
delete q;
}
链队
/*链栈*/
void DestroyQueue(Queue &q)
{
LinkNode p;
while(q.front)
{
p = q.front;//str保存当前删除的结点
q.front = q.front->next;//s指向下一个需要删除的结点;
delete p;
}
}
- 同样链结构只能一个结点一个结点删除。
1.2.8循环队列(顺序表)
- 在顺序队列中,随着不断出队,队头下标不断增大,以q.rear==Maxsize-1为队满条件,实际不够合理,这是假溢出。因为一旦出队,顺序队中就有剩余的空间可进队。
- 而为了解决利用不充分的问题我们使用了循环队列,而当我们使用循环队列时,队空和队满的条件都为rear==front
- 而为了解决队空队满条件相同问题,我们少用一个元素空间,另队头指针指向队头元素的前一个位置。
- 循环队列的重要判断操作
队空条件:q.rear == q.front;
队满条件:(q.rear + 1) % Maxsize == q.front;
而当进队出队的首尾指针移动(以尾指针为例)
q.rear++; => q.rear = (q.rear + 1) % Maxsize;
计算队列长度:
length = (q.rear - q.front + Maxsize) % Maxsize;
1.3栈的应用
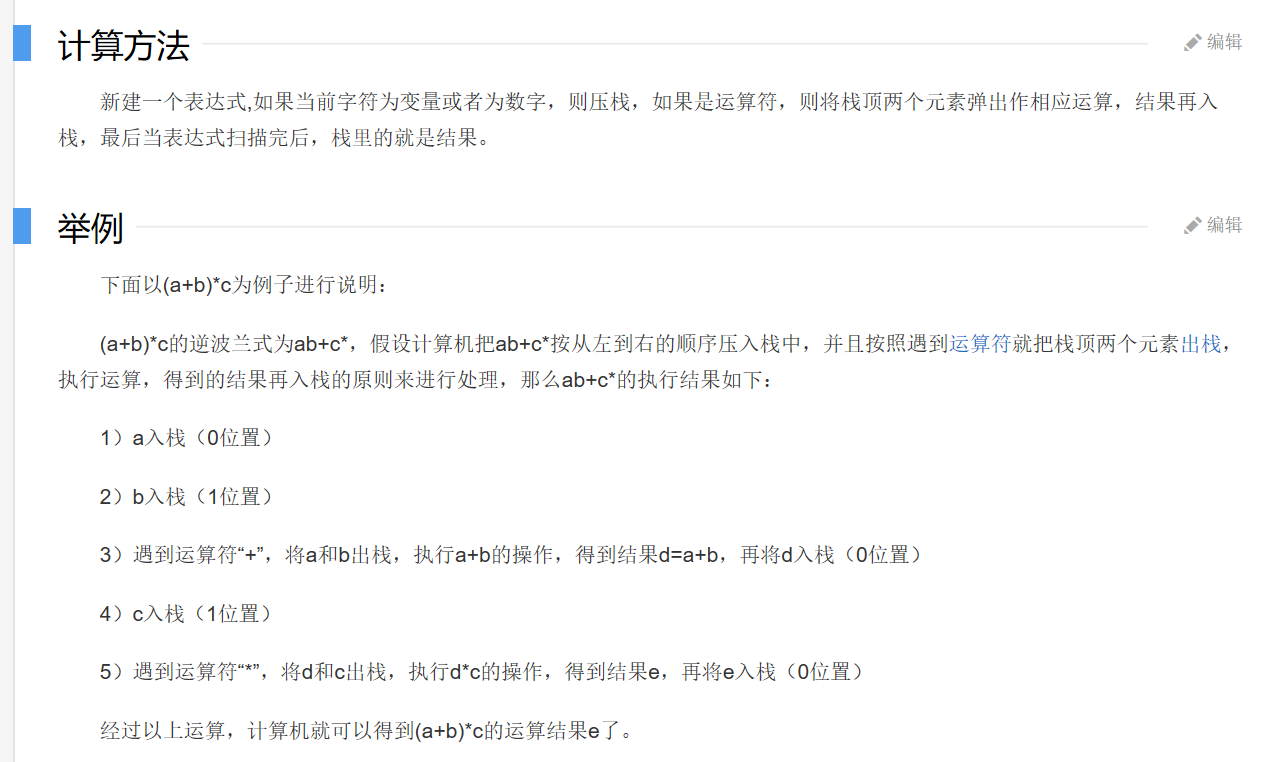
1.中缀表示式转后缀表达式,以及利用后缀表达式进行计算
关于中缀表达式转后缀表达式的转换规则

根据转换规则,分享一个链接帮助理解转换过程:
https://blog.csdn.net/lcl497049972/article/details/83061274
利用后缀表达式进行计算的方法:
2.符号配对(实际上配对匹配类的题目都可考虑用栈处理)
-
关于符号配对我们正是利用的匹配思想。有关符号的配对处理,我们是将左括号入栈内,利用栈的先进后出的特点,正好能与右括号进行一一的匹配比较。
-
同样PTA的7-2 jmu-字符串是否对称,是否对称问题,我们也可将字符串的前半段入栈内,在与后半段一一比较即可。
这里我们学习了一点map的用法:我们利用大约映射的特点,利用map进行匹配

想要更多了解map用法:https://blog.csdn.net/sevenjoin/article/details/81943864
3.数字进制转换
该栈的利用是,曾在课后的测试题中出现(栈的复习测试题-3.填空题)。原题是利用链栈结构实现一个十进制数转换成八进制数的一个填空题。
由此进行改造为十进制数转换为任意进制数的方法:
代码实现
#include <iostream>
#include <stack>
using namespace std;
int main()
{
stack <int>s;
int n, d;
cout << "请输入你要转换的十进制数:";
cin >> n;
cout << "请输入你的目标进制数:";
cin >> d;
while (n)
{
s.push(n % d);
n = n / d;
}
while (!s.empty())
{
cout << s.top();
s.pop();///pop的返回值类型为空
}
return 0;
}
4.迷宫
(有关查找迷宫路径的具体分析放在下面队列中,这里仅对栈的迷宫实现进行简单分析以及与队列的方法的比较)
具体代码实现:
int mgpath(int xi,int yi,int xe,int ye) //求解路径为:(xi,yi)->(xe,ye)
{
int i,j,k,di,find;
StType st; //定义栈st
st.top=-1; //初始化栈顶指针
st.top++; //初始方块进栈
st.data[st.top].i=xi; st.data[st.top].j=yi; st.data[st.top].di=-1;
mg[xi][yi]=-1;
while (st.top>-1) //栈不空时循环
{
i=st.data[st.top].i;j=st.data[st.top].j;di=st.data[st.top].di; //取栈顶方块
if (i==xe && j==ye) //找到了出口,输出路径
{
printf("迷宫路径如下:
");
for (k=0;k<=st.top;k++)
{
printf(" (%d,%d)",st.data[k].i,st.data[k].j);
if ((k+1)%5==0) //每输出每5个方块后换一行
printf("
");
}
printf("
");
//return(1); //找到一条路径后返回1
}
find=0;
while (di<4 && find==0) //找下一个可走方块
{
di++;
switch(di)
{
case 0:i=st.data[st.top].i-1;j=st.data[st.top].j;break;
case 1:i=st.data[st.top].i;j=st.data[st.top].j+1;break;
case 2:i=st.data[st.top].i+1;j=st.data[st.top].j;break;
case 3:i=st.data[st.top].i,j=st.data[st.top].j-1;break;
}
if (mg[i][j]==0) find=1; //找到下一个可走相邻方块
}
if (find==1) //找到了下一个可走方块
{
st.data[st.top].di=di; //修改原栈顶元素的di值
st.top++; //下一个可走方块进栈
st.data[st.top].i=i; st.data[st.top].j=j; st.data[st.top].di=-1;
mg[i][j]=-1; //避免重复走到该方块
}
else //没有路径可走,则退栈
{
mg[st.data[st.top].i][st.data[st.top].j]=0;//让该位置变为其他路径可走方块
st.top--; //将该方块退栈
}
}
return(0); //表示没有可走路径,返回0
}
- 栈的搜索迷宫路径是深度搜索,其就是沿着找到的可走的方块一直不断搜寻。即找到可走方块就进栈,未找到就当前位置退栈。
- 其实际的过程中其搜索路径无法预测,路径很可能就像是我们玩迷宫时,碰到思路返回换个方向重新搜寻的样子,路径可能是返回是重复的。
5.网络浏览器将用户最近访问过的网页组织为一个栈。
6.递归算法也采用了栈的结构。
1.4队的应用
1.求迷宫最短路径:
由于利用队列搜索迷宫路径时,是广度搜索,每走一个方块都会搜寻附近所有的可走方块都会入队中,然后一旦发现找到出口就输出,因此一发现即为最快到达出口的路径。
下面对该做法进行分析:
数据存储结构的定义:

伪代码:

- 将起始位置的pre设为1,可看出是一个出口的标志来使用
如题7-8 电路布线中,关于求路径长度的函数,我们这样写:
void numbox(Queue Q, int pre)
{
int num = 0;
do
{
num++;
pre = Q.data[pre].pre;
} while (pre != -1);
num++;
cout << num;
}
以方块pre为-1为循环结束条件,即回溯到了起始位置,然后起始位置也算一个长度,所以num++;
-
关于起始位置迷宫设为-1 ,其实和下面一样,一旦入队的方块的迷宫值都设为-1,这是为了避免重复搜索,由于判断是否可走的条件是利用迷宫值是否为0,因此我们改变其值。
与栈搜索方法不同,由于我们使用的是广度搜索能够找出最短路径,为了是找到最短路径,因此我们就应该避免方块重复入队。 -
循环先让队头出队,一开始的时候不是很明白为什么要一边入队一边出队,后面看注释才慢慢理解明白。让出队元素判断是否是出口,一边找寻该位置附件可走位置。
出队意义:
一在于,一边循环不断地对队中地每个方块进行判断,因为只有出队我们才可遍历一下这个队列。
二则是,与记录方块的上一位置紧密相连。 -
下面即对 记录方块上一位置操作分析:由于我们的队头指针是指向元素的上一位置,当我们出队时,指针位置即为出队的位置。而我们后面进行找寻该出队位置附近可走位置时,要记
录可走方块的上一位置时,即为该出队方块的位置。
因此不断出队另一方面也是,确保了 入队方块的来源关系pre 与 队头指针位置 的统一性。 -
而我们需要输出路径时,则又是利用了顺序队出队实际并未出队的特点,也就是虽然一直在出队判断寻找,但实际都还在队中,根据每一个方块的pre,我们就可以不断回溯直到出口位置。
2.报数问题:报到某数m时的人出队
这里我们以PTA题-7-6 jmu-报数游戏 进行分析
伪代码:

- 该解决问题的主要思想就是:未报到数的人继续排到队伍的最后,因此循环不断地对每一个人进行判断,若不符号就将队头先入队,再将队头出队
1.3谈谈你对栈和队列的认识及学习体会。
学习体会:
- 刚学栈和队列的时候感觉虽然概念都能看得懂,但是到了应用部分就没那么容易了。一开始是利用栈来解决计算表达式问题,一开始看课件都不是很懂,是百度搜索了一些中缀怎样转后缀的
资料才慢慢搞懂。还有关于栈和队列分别用于解迷宫的应用,以及pta中队列的银行问题,感觉比以前的题目都难了一些,要花比较多的心思取构思调试。
一些学习认识:
-
*一个易错点 *:关于'.'和'->'的使用。
这是在复习测试题中出现,当我们要表示的是结构体成员时用'.',而当我们已经有结构体指针时,则可以使用'->'来指向结构体成员。
错误分析:
之所以我们混淆会都使用'->',是因为我们之前在链表部分,由于头结点啊、每个结点我们都是用指针来定义,因此相关每个结点的操作我们也都是直接使用'->'来做
而如今有如栈的部分,例如顺序栈,顺序栈的结构体成员中包含顺序数组,和top指针,而当我们需要使用定义时,仅仅只是定义了这个结构类型来使用,而不是用指针,因此就不能用'->'. -
一个易错点:关于栈空,队空问题
在学习出栈和出队的基本操作函数过程中,我们会强调先要判断是否空的问题。
而当我们在实际的一些问题中,由于我们常使用stl容器,在每一次的操作时,我们都应有意识地判断是否可能栈空。
例如,可能while循环条件以栈空为结束条件,循环操作是一次出栈,这样正确地就是不断出栈。而实际问题中在这样地一个while循环中,根据需要我们可能会有多次地出栈操作,但是经常
很容易忘记,* 每一次 *出栈操作都先要判断 -
关于队列的出队
在链表中我们利用指针来进行遍历,在数组中我们利用下标进行遍历。而在报数问题中,我们不断的对队列中的队头进行判断出队进队操作,实际上队列的不断出队操作最后就相当是遍历了队
列,在队列的不断出队推动后移。有如 顺序队中的出队就像数组的遍历,数组遍历我们通常用i++通过下标变化遍历,我们利用则是头指针后移,实质上上一样的,因为顺序队本身就利用的数
组的存储结构。
2.PTA实验作业
2.1.题目1:7-5表达式转换
2.1.1代码截图
#include<iostream>
#include<stack>
#include<string>
#include<map>
using namespace std;
bool IsNumber(char ch);
int main()
{
string str;
stack<char> S;
int len, i;
int flag = 0,symbol=0;//flag表示是否已经输出第一个字符,symbol表示是否是正负符号
map<char, int> mp;//设置优先级
mp['+'] = mp['-'] = 1;
mp['*'] = mp['/'] = 2;
mp['('] = 3;
cin >> str;
len = str.size();
for (i = 0; i < len; i++)
{
if (IsNumber(str[i]) || str[i] == '.')//若为数字或小数点就直接输出
{
if (flag == 0|| symbol == 1 || IsNumber(str[i - 1]) || str[i - 1] == '.')//第一个输出,前一个为正负符号,前一个为数字或‘.’
{
cout << str[i]; flag = 1;
}
else cout << " " << str[i];
}
else if ((str[i] == '-' || str[i] == '+') && i == 0 || (str[i] == '-' || str[i] == '+') && str[i - 1] == '(')//为第一个符号或减号前有左括号即为负号
{
if (str[i] == '-')
{
symbol = 1;
if (flag == 0)
{
cout << str[i]; flag = 1;
}
else cout << " " << str[i];
}
}
else//即为运算符时
{
symbol = 0;
if (S.empty()) S.push(str[i]);//若栈空则直接进栈
else
{
if (str[i] == ')')//若为右括号则输出左括号前的符号
{
while (!S.empty()&&S.top() != '(')
{
cout << " "<<S.top(); S.pop();
}S.pop();//左括号也要出栈
}
else if (S.top() == '(') S.push(str[i]);//若栈顶为左括号则无条件进栈,该情况不符合优先级情况另作讨论
else//根据比较优先级
{
if (mp[str[i]] > mp[S.top()]) S.push(str[i]);
else
{
while (!S.empty() &&S.top()!='('&& mp[str[i]] <= mp[S.top()])
{
cout << " "<<S.top(); S.pop();
}//将所以小于等于的输出,并且最后将该符号入栈
S.push(str[i]);
}
}
}
}
}
while (!S.empty())
{
cout <<" "<< S.top();
S.pop();
}
}
bool IsNumber(char ch)
{
int number=ch-'0';
if (number <= 9 && number >= 0) return true;
else return false;
}
2.1.2本题PTA提交列表说明。
(该提交列表还算短,但在完全正确之前,在自己调试的时候实际上也花了很多时间,因此记录一下该题做的过程中的错误)
-
1.一开始只是按照伪代码正确的将表达式转换为后缀表达式,但没注意到空格输出,因此对空格输出的条件开始进行改代码:
首先是通过第一个输出的字符不带空格输出,后面的都带空格输出,因此添加了flag变量来表示是否为第一个输出的数。
(而由于第一个输出的只可能是判断为正负号的字符或者是数字,因此对于flag的判断我们只在这两种情况中做。即判定为运算符时,输出时一定不是第一个,直接输出时带空格即可) -
2.此外在该位置字符判定为数字时,还需考虑实际可能是不止一位的数字,带小数点的数字,带正负号的数字。因此都要另行判断后输出不带空格的数字。
因此在数字部分需判断判断,若前为正负符号,或者前为小数点,我们也是不带空格输出。 -
3.还有关于正负符号的判断:第一个为字符为加减号,或是加减后前有左括号都是正负号
经过判断后只有为负号时要输出,写的时候因为想着只用减号输出所以把判断条件中的正号判断去掉了,但经过调试,表达式中还是会可能出现正号,所以判断条件必须是正号和负
号都判断,在判断中在判断是否负号输出。 -
4.部分错误中一个是运算符前有正负。错误原因是:写右括号时,将左括号前的都出栈操作写法不够严谨。While循环时不止应将左括号作为限制条件,还需先判断是否栈空。同样的错误也
在比较栈顶优先级,低于或等于就出栈,用while循环控制时同样需要先判断是否栈空。说明某些情况下先要判断是否栈空的条件。这种意识仍不够高。 -
5.部分错误中另一个错误是:嵌套括号。错误原因是:比较优先级判断是否出栈是不够严谨。因为在比较栈顶优先级时,低于或等于栈顶就出栈,这个操作必须是与左括号前的符号相比。否
则由于优先级关系,其他符号都低于左括号优先级,此时就会将左括号出栈,这是错误的。因此比较时修改前提条件。 -
6.其他代码思路,由实验课上的同学讲解得:可以将栈外和栈内的优先级分开设置。这样一来对于运算符的判断然后操作这一部分就会简单很多,因为大多设置都是由于受限于优先级的
影响。
2.2.题目2:7-4 符号配对
2.2.1代码截图
#include<iostream>
#include<stack>
#include<map>
#define max 200
using namespace std;
int main()
{
char str[max];
stack<char>S;
int i, j = 0;
char ch;//用来记录未找到匹配的符号
map<char, char> mp;
int flag = 1;
mp[']'] = '['; mp['}'] = '{'; mp[')'] = '(';//!!!!!!!
mp['*'] = '*'; mp['/'] = '/';
while (1)
{
cin.getline(str, max);
if (str[0] == '.' && (!str[1])) break;//循环读入字符直至结束
i = 0;
while (str[i])
{
if (str[i] == '(' || str[i] == '{' || str[i] == '[')
{
S.push(str[i]);//左括号进栈
}
else if (str[i] == '/' && str[i + 1] == '*')//两个字符都需进栈
{
S.push(str[i]);
i++;
S.push(str[i]);
}
else if (str[i] == '}' || str[i] == ']' || str[i] == ')')
{
if (!S.empty() && mp[str[i]] == S.top())//前提栈不空才匹配
{
S.pop();
}
else
{
if (flag == 1) { flag = 0; ch = str[i]; break; } //不匹配
}
}
else if (str[i] == '*' && str[i + 1] == '/')
{
if (!S.empty() && mp[str[i]] == S.top())//若不匹配
{
S.pop(); i++;
if (!S.empty() && mp[str[i]] == S.top())
{
S.pop();
}
else
{
if (flag == 1) { flag = 0; ch = '*'; break; }//不匹配
}
}
else
{
if (flag == 1) { flag = 0; ch = '*'; break; }//不匹配
}
}
i++;
}
}
if (S.empty() && flag == 1) cout << "YES";
else
{
if (S.empty())
{
if (ch == '*') cout << "NO" << endl << "?-*/";
else cout << "NO" << endl << "?-" << ch;
}
else//栈未空
{
if (S.top() == '*')cout << "NO" << endl << "/*-?";
else cout << "NO" << endl << S.top() << "-?";
}
}
}
2.2.2提交列表及说明

1.一开始答案错误也是对输出格式没有控制好,对于如何记录未匹配成功的符号进行改动。分为两种情况:
一是右括号未匹配对,即栈不空情况下。此时匹配未成功我们直接用ch记录。二是左括号未匹配成功,即结束了栈不空,此时取栈顶即为未匹配成功符号。由于是要第一个未匹配成功的,因此又引入了flag,来表示是否为第一个不匹配的符号。
2.一些大大小小的错误主要还是在调试中修改的,本题相比于之前的符号配对,难点在于‘/’的判断是两个字符组成,因此只能另外分情况判断。
有如‘/’的判断,判断时要排除单独的‘’‘/’,进栈时要都进栈。
‘/’的与栈中比较时,只有两个字符都匹配才算匹配,否则都算不匹配。
还有关于输出时,一开始还纠结不匹配时将这两个字符都存入,记录的不匹配字符需要分情况,会比较麻烦。因此最后只使用一个‘*’来作为不匹配符号,输出时自行控制输出样式就好
3.阅读代码
3.1 题目及解题代码
题目:验证栈序列
实际上就是以pushed序列为进栈顺序,判断popped的序列有没有可能是其出栈的顺序

解题代码:
class Solution {
public:
bool validateStackSequences(vector<int>& pushed, vector<int>& popped) {
int n=popped.size(); /*获取序列的大小*/
stack<int> s;
int k=0;
for(int i=0;i<n;i++)
{
s.push(pushed[i]);
/*三个条件的顺序很重要*/
while((!s.empty())&&(k<n)&&(s.top()==popped[k]))
{
s.pop();
k++;
}
}
if(!s.empty()) /*如果非空,则返回false*/
{
return false;
}
return true;
}
};
3.1.1 该题的设计思路
-
该题的解题思路其实较好理解,就是相当于模拟pushed序列的进栈出栈过程,来判断该popped序列是否正确。
-
具体设计思路:
-
1.引入一个栈stack
-
2.把pushed序列按顺序放到栈stack中,每放一个数据对比栈顶与序列popped中元素是否相同,若相同,则栈stack执行pop操作,移到popped的下一个元素,继续对比栈顶与该元素是否相同。
图示模拟过程:
3.1.2 该题的伪代码

3.1.3 运行结果
pushed = [1,2,3,4,5], popped = [4,5,3,1,2] 结果应为false;
pushed = [1,2,3,4,5], popped = [4,3,5,2,1] 结果应为true;

3.1.4分析该题目解题优势及难点。
-
该解题优点在于思路清晰好懂,验证栈序列。该思路就是直接借助栈按照popped序列来模拟出栈过程,比较匹配。
-
难点在于思路简单,但是代码实现起来,如果没有已有的模板,可能没有那么快就理清实现过程。就是想的容易,写起来思路需要考虑的周全。
-
分析一下一些解题思路:
根据栈时进时出的特点,因此我们一遍将pushed序列一个个进栈时,一边就需比较popped序列,是否已经要出栈了。
while中的三个条件顺序,在栈不空,剩余要比较的序列也不空情况下,我们才能比较栈顶和当前比较的popped元素。
若栈不空就返回false。这是因为若是匹配的话,栈中元素最终会在while循环中都出栈,因此会变成空栈。且栈不空时,此时栈顶元素,正说明了popped序列出错的地方。
3.2 题目及解题代码
题目:验证栈序列
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。

解题代码:
class MinStack {
public:
/** initialize your data structure here. */
stack<int> s_data;//存放数据
stack<int> s_min;//存放每一次压入后,栈内的最小值
MinStack() {
}
void push(int x) {
s_data.push(x);
if (s_min.size() == 0) s_min.push(x);
else
{
if (x < s_min.top()) s_min.push(x);
}
}
void pop() {
if (s_data.size() == 0) return false;
s_data.pop();
}
int top() {
return s_data.top();
}
int min() {
return s_min.top();
}
};
3.2.1 该题的设计思路
- 借助一个辅助栈,s_min,在每次s_data压入数据后,与s_min的top进行比较,如果比s_min当前的top的大,则将该数据压入到s_min中,如果s_min的top更大,则将top压入到s_min中
3.2.2 该题的伪代码

3.2.3运行结果

3.2.4分析该题目解题优势及难点。
-
本题难点:本题难点: 普通栈的 push() 和 pop() 函数的复杂度为 O(1);而获取栈最小值 min() 函数需要遍历整个栈,复杂度为 O(N) 。
-
优点:该解题思路清晰,s_data保留原始的栈顺序,而s_min则保留每一次进栈后目前最小值。
-
每次进栈时只与s_min比较一次即可,保证了push操作的时间复杂度仍为O(1),根据操作特点,min即取s_min的栈顶,也保证了min函数的时间复杂度为O(1).
实际上与普通遍历栈的方法相比,时间复杂度是小了,但实际上也牺牲了空间,空间复杂度为o(n). -
注意pop函数写的时候必须两个栈的栈顶都要出栈,而s_min栈中仍保留降序,因此出栈后的栈顶仍为s_data的最小值。