DS博客作业03--树

0.PTA得分截图

1.本周学习总结

二叉树

简单概念部分

• 定义：二叉树或为空树，或由一个根结点和至多两根称为根的左右子树组成的二叉树。
• 特点：不存在度大于2的结点，并且有左右子树之分。
• 满二叉树定义：在一支二叉树中的所有分支结点度都为2，并且叶结点都集中在二叉树的最下一层
• 完全二叉树定义：与完全二叉树相似，但最底层并非全满，允许最底层右边缺少连续若干个结点

二叉树性质及其结点计算部分

• 高度为h的满二叉树恰好有2^h - 1 个结点。

完全二叉树:

• n1 = 0或者n1 = 1。n1可由n的奇偶性确定：
  n为奇数  n1 = 0
  n为偶数  n1 = 1

• 在顺序存储结构中：若i≤n / 2，则编号为i的结点为分支结点，否则为叶结点。

• 完全二叉树结点计算：
  由于完全二叉树最底层却允许在右边缺少连续若干个结点。
  深度为h的完全二叉树的结点个数应为：2^(h - 1) - 1 < n <= 2^h - 1

二叉树的存储结构

二叉树的顺序存储（简单了解）

• 即用数组来存储二叉树的每个结点，利用其数组下标编号来确定其父子关系。

定义如下：

typedef  ElemType  BTree[MaxSize];

其建树过程

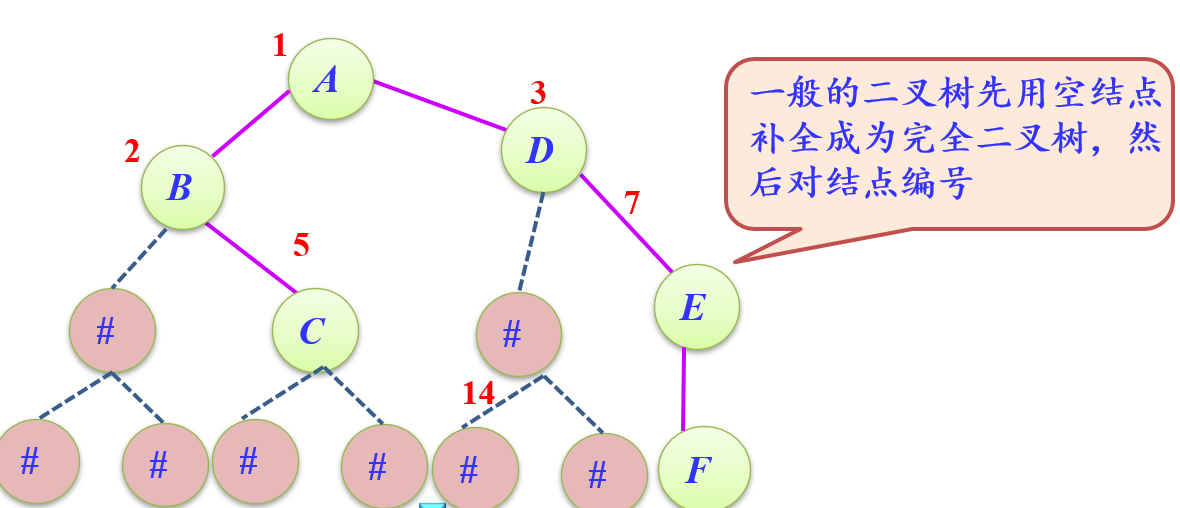
• 注意下标0不用于存储(0参与计算无意义，也就无法确定父子关系，因此不用)

其下标为i的结点，父子关系如下

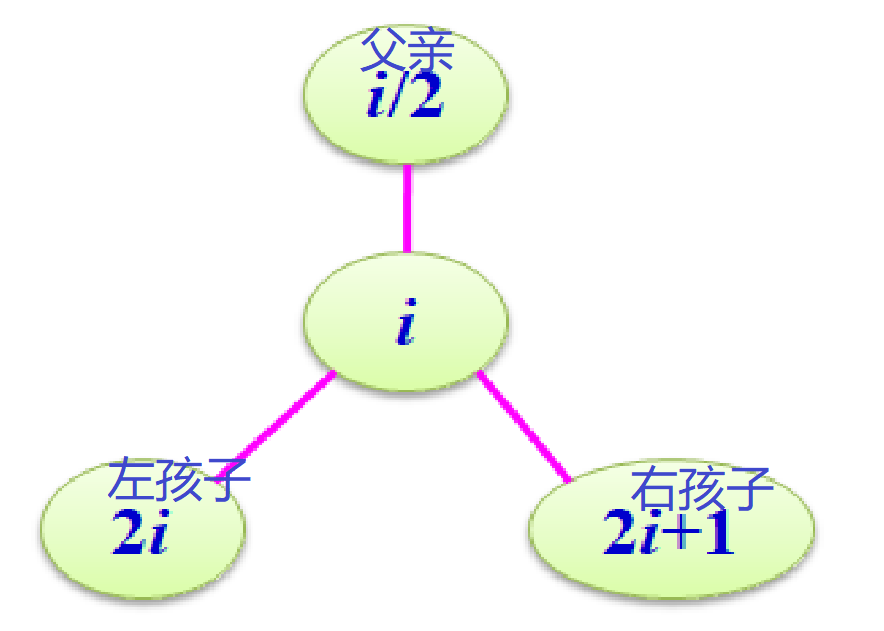
• 实际上我们很少使用顺序存储这种方式来存储二叉树，且进行树的操作。(缺点如下)

  首先由于维持数组下标的计算关系决定父子关系，除了满二叉树，绝大部分二叉树用顺序存储时都会浪费大量的数组空间。

  其次由于数组这种存储方式本身的限制，当我们进行一些树的操作，插入结点删除结点，就要对数组进行移动，其花费成本较大，并不好操作。

二叉树的链式存储

常用的二叉树孩子链存储方式

typedef struct node {
	ElemType data;
	struct node* left, * right;
}BTnode, * BTree;

如图理解将二叉树转成链式结构

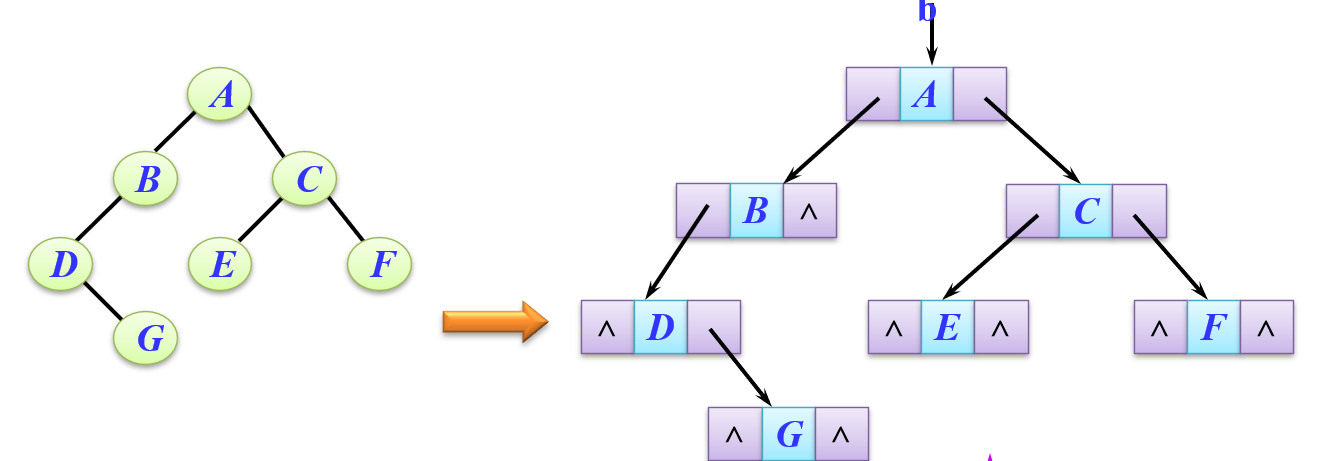
• 通过孩子指针我们可以探知每个结点的左右孩子

• 度为1或0的结点就会出现孩子指针指向空

二叉树的遍历

1.先序遍历：先根再左后右

void PreOrderPrint(BTree BT)
{
	if (BT != NULL)
	{
		printf(" %c", BT->data);
		PreorderPrint(BT->left);
		PreorderPrint(BT->right);
	}
}

2.中序遍历：先左再根后右

void InOrderPrint(BTree BT)
{
	if (BT != NULL)
	{
		InOrderPrint(BT->left);
		printf(" %c", BT->data);
		InOrderPrint(BT->right);
	}
}

3.后序遍历：先左再右后根

void PostOrderPrint(BTree BT)
{
	if (BT != NULL)
	{
		PostOrderPrint(BT->left);
		PostOrderPrint(BT->right);
		printf(" %c", BT->data);
	}
}

注意：无论先序中序后序遍历都是访问结点两次，由于该函数调用采用递归方式，调用时一次返回时一次

4.层次遍历：层层遍历，从左到右

伪代码设计思路

具体代码实现过程

void LevelTraversal(BTree BT)//层次法遍历利用队列
{
	queue<BTree>Q;
	BTree node;

	if (BT)//判断是否空树
	{
		Q.push(BT);//根结点先入队
	}
	else
	{
		cout << "NULL"; return;
	}

	while (!Q.empty())
	{
		node = Q.front();//保存队头
		Q.pop();//出队
		cout << node->data
		
		if (node->left)
		{
			Q.push(node->left);
		}
		if (node->right)
		{
			Q.push(node->right);
		}
	}
}

注意此处队列类型的定义：queueQ

该队列应当是将结点存入队列，而不仅仅是该结点的data。(刚开始编程时的错误)

二叉树的构造

1.顺序存储转二叉树

前提注意：顺序存储时先要把二叉树补成满二叉树后，得到其对应字符串，该建树函数根据该字符串进行处理建树

如：

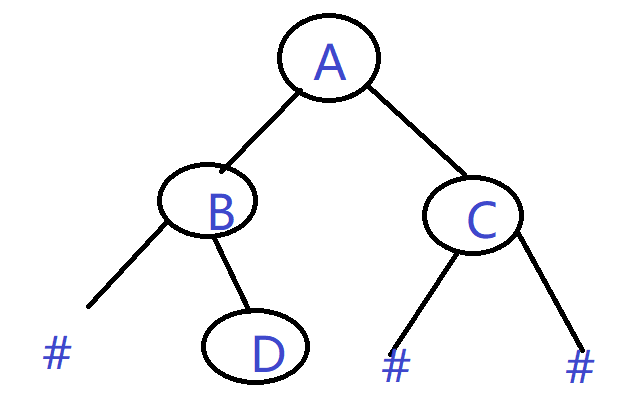
其对应的字符串为：“#ABC#D##” (str[0]不用)

具体实现过程

• 两种类型皆需考虑，字符串遍历完，或结点为“#”的情况。

void类型函数

void CreateBTree(BTree& BT, string str, int i)
{
	int len;
	len = str.size();
	if (i > len || str[i] == '#')
	{
		BT = NULL; return;
	}

        BT = new BTnode;
	BT->data = str[i];
	CreateBTree(BT->left, str, 2 * i);
	CreateBTree(BT->right, str, 2 * i + 1);
}

• 注意BTree& BT，建树过程会对结点进行改变

注意函数类型是void若为空情况，不能返回NULL，也不能直接返回，结点要先赋空，再返回

BTree类型

BTree CreatBTree(string str, int i)
{
	BTree BT;
        int len = str.size();
        if (i > len - 1 || str[i] == '#') return NULL;

	BT = new BTnode;
	BT->data = str[i];
	BT->left=CreatBTree( str, 2 * i);
	BT->right=CreatBTree(str, 2 * i + 1);
	return BT;
}

2.先序遍历建树

注意前提：顾名思义，该方法是按照先序遍历的顺序建树，因此补二叉树时与顺序存储不同，并非是补全，而是将所有的结点都补全为度为2.

如：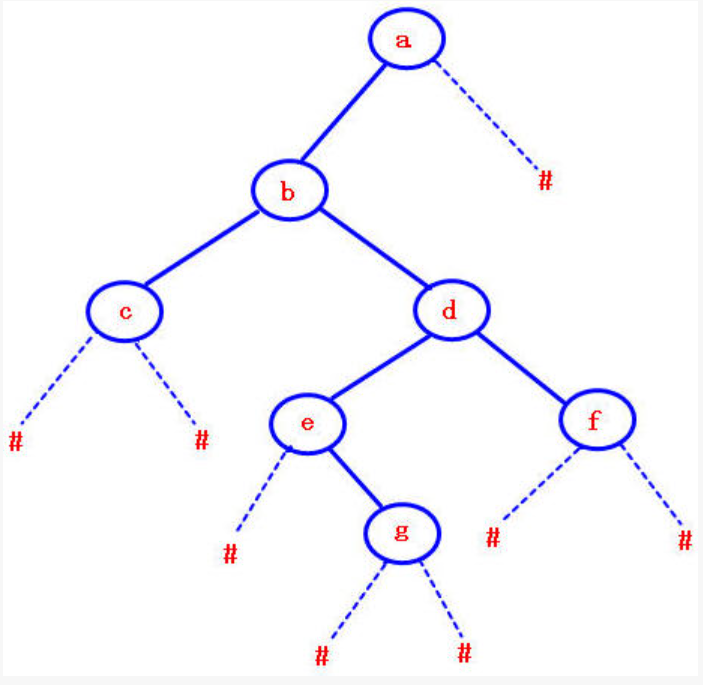

其所获得前提字符串为：“abc##de#g##f###”

代码具体实现过程：

BTree CreateTree(string str, int& i)//先序遍历建树
{
	BTree bt;
	int len =str.size();
	if (i > len - 1 || str[i] == '#')return NULL;

	bt = new BTnode;
	bt->data = str[i];
	bt->lchild = CreateTree(str, ++i);
	bt->rchild = CreateTree(str, ++i);
	return bt;
}

• 总体而言大致步骤与顺序转存储相差不大需注意的是，调用时++i。（由于按照先序遍历顺序，其左右孩子的关系就是++i）

• 注意函数头int& i ，正是由于先序遍历顺序，调用左孩子递归后返回，右孩子的i值是应为改变后的，因此& i （可变）.

3.层次遍历建树

• 其设计思路与迷宫大致相同，利用队列,进行一层层的入队遍历

其补全二叉树也是将结点补为度为2，得到到的字符串顺序则是按照层次遍历

如：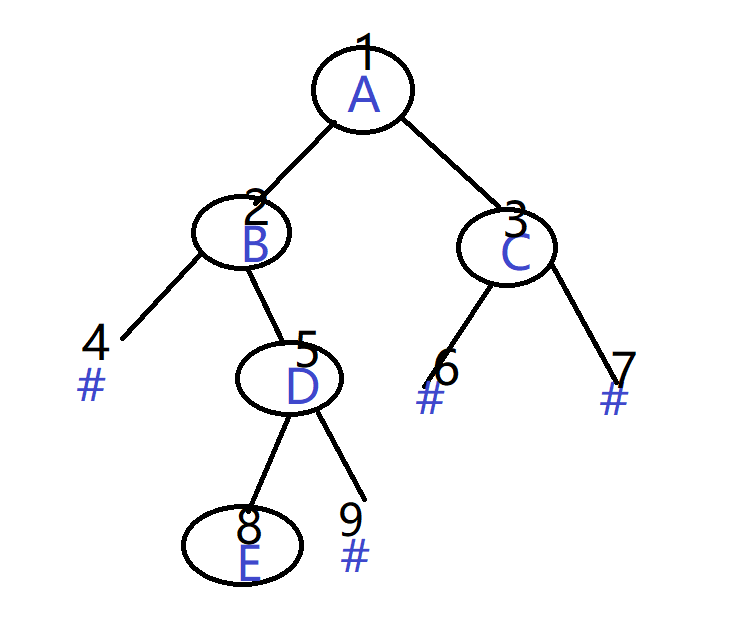

其得到的字符串就为："ABC#D##E#"

伪代码过程：

具体代码实现过程：

void CreatBTree(BTree& BT, string str)
{
	queue<BTree> Q;//队列是树结点类型
	BTree node;//树的每个结点
	int i = 0, len = str.size();

	BT = new BTnode;//创根结点并入队
	BT->data = str[i];
	Q.push(BT);

	while (!Q.empty())
	{
		node = Q.front();
		Q.pop();

		i++;//判断左孩子
		if (i>=len-1||str[i] == '#') node->left = NULL;
		else
		{
			node->left = new BTnode;
			node->left->data = str[i];
			Q.push(node->left);
		}
	
		i++;//判断右孩子
		if (i >= len - 1 ||str[i] == '#')node->right = NULL;
		else
		{
			node->right = new BTnode;
			node->right->data = str[i];
			Q.push(node->right);
		}
	}
}

• **注意结束标志是由队空决定，而不是字符串遍历结束！！！！，否则最后一层的结点就无法处理完全 **

具体实现过程中注意条件判断：i >= len - 1 ，基于对字符串遍历完毕的判断，仍赋为NULL

4.先序中序建树

根据其特点：先序序列第一个为根结点，因此在中序找到根结点，就可区分左右子树

具体代码

BTree  CreateBT(char* pre, char* in, int n)
{
	BTree s;  char* p;  int k;
	if (n <= 0) return NULL;
	s = new BTnode;
	s->data = *pre;//创建节点并赋值             
	for (p = in; p < in + n; p++)      //找到在中序中s的位置指针p
		if (*p == *pre) break;

	k = p - in;//通过p计算中序中该位置到头的长度

	s->left = CreateBT(pre + 1, in, k);//构造左子树
	s->right = CreateBT(pre + k + 1, p + 1, n - k - 1);		 //右子树
	return s;

• 函数头第一个参数为构造部分的先序序列，中序序列，以及序列长度

• 根据先序先根的特点，我们取结点就为目前先序序列的首个字符即*pre

• 先找到中序中当前结点位置指针p，再通过p计算出，该位置到中序首位置的长度。
  通过k，就可分出先序和中序的根以及左右子树了.

• 构造左子树部分：
  先序序列中左子树部分从pre+1开始。
  中序顺序是左先，因此左子树在中序中的序列仍旧是从in开始。
  左子树序列长度即为k（中序根之前都为左，由计算得k）。

• 构造右子树部分：
  先序序列中右子树部分从pre+1 +k,（左子树开始加上左子树序列长度即为右子树开始的部分）。
  中序序列中右子树部分即从当前结点位置p后开始，所以是p+1。
  右子树序列长度为n-k-1（序列总长-左子树序列长度-根结点，剩下的即为右子树长度）。

• For循环限制：
  在中序中找到结点位置，因此从头开始，所以from p=in。
  中序序列长度为n,因此限制到p=in+n-1 查找。（即到中序序列的最后一个位置）

5.后序中序建树

根据其特点：后序的最后一个为根结点，在中序中找到根结点后，就可区分左右子树

BTree CreateBT(int* post, int* in, int n)
{
	BTree s; int* p;  int k;
	if (n <= 0) return NULL;
	s = new BTnode;//创建节点
	s->data = *(post + n - 1);        //构造根节点
	for (p = in; p < in + n; p++)//在中序中找为s的位置k
		if (*p == *(post + n - 1)) break;
	k = p - in;

	s->left = CreateBT(post, in, k);	//构造左子树
	s->right = CreateBT(post + k,in + k + 1, n - k - 1);//构造右子树
	return s;
}

6.二叉树的销毁

具体代码

void DestroyBTree(BTree BT)//先序遍历销毁树
{
	if (BT != NULL)
	{
		DestroyBTree(BT->left);
		DestroyBTree(BT->right);
		delete BT;
	}
}

注意只可能是先序遍历销毁树，因为我们是通过根结点才知其左右孩子，若是先删除左右孩子，就找不到根或另一个孩子了。

二叉树的应用

树

• 树的性质：

• 1.树中的结点数等于所有结点的度数之和加1.

• 2.度为m的树中第i层上至多有mi - 1个结点（i≥1）.

树的结构定义(常见类型)

1.双亲存储结构

typedef struct
{
	ElemType data;	//结点的值
	int parent;		//指向双亲的位置
} BTree[MaxSize];



2.孩子链结构

typedef struct node
{
	ElemType data;		  //结点的值
	struct node* sons[MaxSons];	      //指向孩子结点
}  BTreeNode;



3.兄弟孩子链结构

typedef struct tnode
{
	ElemType data;	//结点的值
	struct tnode* son;  	//指向兄弟
	struct tnode* brother;  //指向孩子结点
} BTeeNode;

树的遍历

• 1.先根遍历

• 2.后根遍历

• 3.层次遍历

• 由于只有二叉树有左右子树之分，因此树的递归遍历时只有先根和后根

二叉树与树、森林的相互转换

• 森林、树转换为二叉树：
  1.相邻兄弟节点加一水平连线
  2.除了左孩子和叶子节点，删掉连线
  3.水平连线以左边节点轴心旋转45度

• 二叉树还原为一颗树：
  1.任一节点k，搜索所有右孩子
  2.删掉右孩子连线
  3.若节点k父亲为k0，则k0和所有k右孩子连线

线索二叉树

• 基本概念：

  二叉链存储结构时，每个节点有两个指针域，总共有2n个指针域。

  有效指针域：n - 1（根节点没指针指向）
  空指针域：n + 1

  利用这些空链域, 指向该线性序列中的“前驱”和“后继”的指针，称作线索。

• 结点结构
  若左右有孩子，则指针指向其孩子，若无孩子，则分别指向其前驱后继。添加两个标志域，来区别是否指孩子。
  

• 线索由顺序决定，先序中序或是后序
  线索用虚线表示.

• 中序线索树中可能出现头尾悬空，为防止悬空，增设头结点：

  1.头结点左孩子指向根节点
  2.右孩子为线索，指向最后一个孩子
  3.遍历序列第一个结点前驱为头结点，最后一个节点后继为头结点

• 注意：中序线索二叉树可以找到对应树每个节点的前驱和后继节点。先序和后序线索二叉树无法做到。

• 中序线索二叉树好处在于遍历二叉树不需要递归，所有节点只需遍历一次！！

哈夫曼树

• 定义：设二叉树具有n个带权值的叶子节点，那么从根节点到各个叶子节点的路径长度与相应节点权值的乘积的和，叫做二叉树的带权路径长度。
  而具有最小带权路径长度的二叉树称为哈夫曼树。

• 构造哈夫曼树的原则：
  权值越大的叶结点越靠近根结点。
  权值越小的叶结点越远离根结点。

• 构造哈夫曼树的过程：
  （1）根据给定的n个权值{ w1,w2,……wn }，构造n棵只有根结点的二叉树。F = { T1，T2，…，Tn }。
  （2）在F中选取根结点的权值最小和次小的两棵二叉树作为左、右子树构造一棵新的二叉树，这棵新的二叉树根结点的权值为其左、右子树根结点权值之和。
  （3）在集合F中删除作为左、右子树的两棵二叉树，并将新建立的二叉树加入到集合F中。
  （4）重复（2）、（3）两步，当F中只剩下一棵二叉树时，这棵二叉树便是所要建立的哈夫曼树。

-图示过程：例 {2 3 4 6}

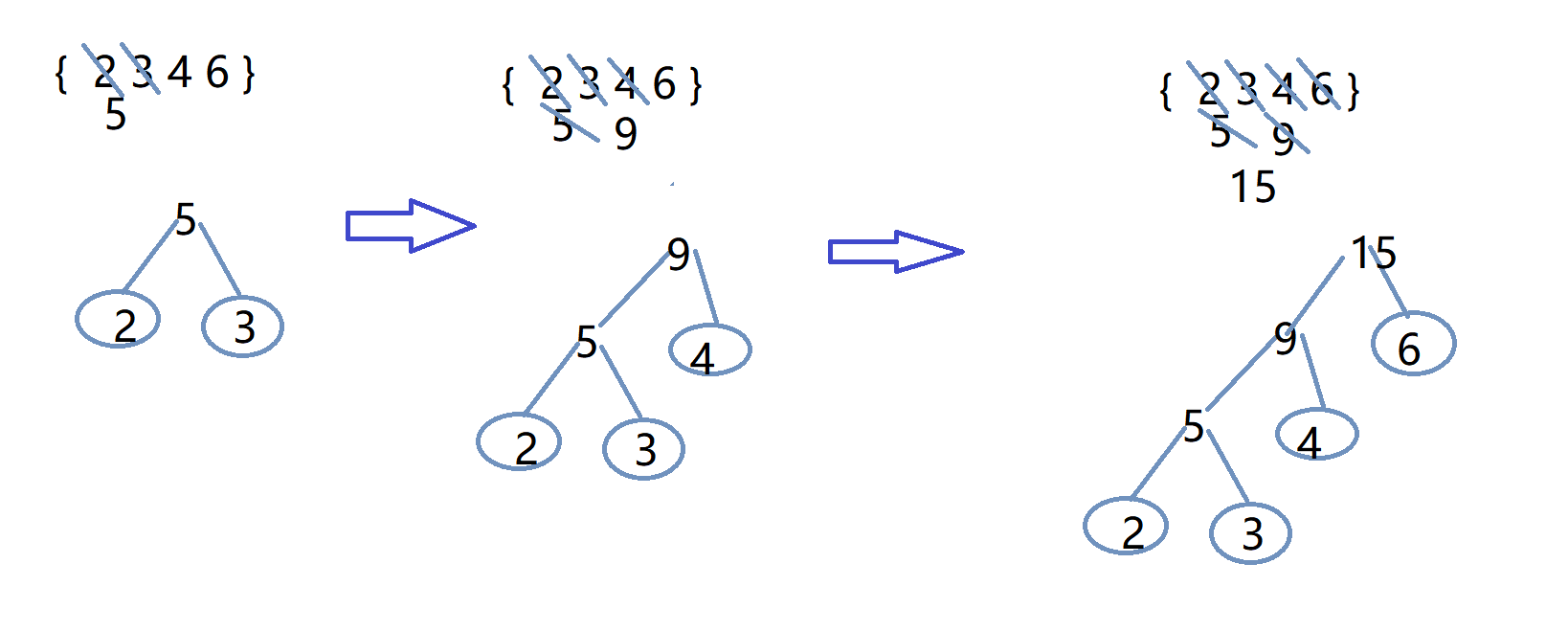
• 注意生成后的结点权值也要再放入序列中进行比较

结构体定义

typedef struct node {
	float weight;
	int parent;
	int lchild;
	int rchild;
}HTnode;

在结点较多情况下，数组最好改为在堆区申请

具体代码

#include<iostream>
#define max 10000
using namespace std;
typedef struct node {
	float weight;
	int parent;
	int lchild;
	int rchild;
}HTnode;
void CreatHtree(HTnode *HT, int n);/建哈夫曼树
void Calculate(HTnode *HT, int n);//计算权值
int main()
{
	HTnode* HT;
	int n;//叶子结点数
	cin >> n;
	HT = new HTnode[2 * n - 1];

	for (int i = 0; i < n; i++)
	{
		cin >> HT[i].weight;
	}
	CreatHtree(HT, n);
	Calculate(HT, n);
	
}
void CreatHtree(HTnode *HT, int n)
{
	int i, j, lnode, rnode;
	float min1, min2;

	for (i = 0; i < 2 * n - 1; i++)
	{
		HT[i].parent = -1;	HT[i].lchild = HT[i].rchild = -1;//初始化，后用于判断是否已经用于生成根  	
	}
	for (i = n; i < 2 * n - 1; i++)//构造非叶子结点,for循环为非叶子结点在数组中的范围
	{
		min1 = min2 = 1000000;//每次遍历查找前都将min重新赋值
		rnode = lnode = -1;
		for (j = 0; j < i; j++)//从已生成的结点中查找，每生成非叶子结点，也要列入遍历查找的范围
		{
			if (HT[j].parent == -1)//从未有父母的结点中查找，即未利用于生成根
			{
				if (HT[j].weight < min1)//小于最小值
				{
					min2 = min1; min1 = HT[j].weight;
					rnode = lnode; lnode = j;
				}
				else if (HT[j].weight < min2)//小于次小值
				{
					min2 = HT[j].weight;
					rnode = j;
				}
			}
		}//遍历完后找到最小和次小，由此生成根结点.
		HT[lnode].parent = HT[rnode].parent = i;//只有在遍历之后才可确定最终的最小次小，才能进行此操作，不能在遍历同时赋父母值
		HT[i].weight = HT[lnode].weight + HT[rnode].weight;
		HT[i].lchild = lnode; HT[i].rchild = rnode;
	}
}

void Calculate(HTnode *HT, int n)
{
	int i;
	int num=0;
	for (i = n; i < 2 * n - 1; i++)//非叶子结点权值总和
	{
		num+= HT[i].weight;
	}
	cout << num;
}

注意计算权值时，可利用非叶子结点的权重总和这一特点

并查集

• 基本概念：
  查找一个元素所属的集合及合并2个元素各自专属的集合等运算。（常应用于朋友圈）
  在并查集中，每个分离集合对应的一棵树，称为分离集合树。整个并查集也就是一棵分离集合森林。

• 并查集的主要操作

Union(Root1, Root2)   //合并操作
Find(x)                          //查找操作
UFSets(s)                      //构造函数

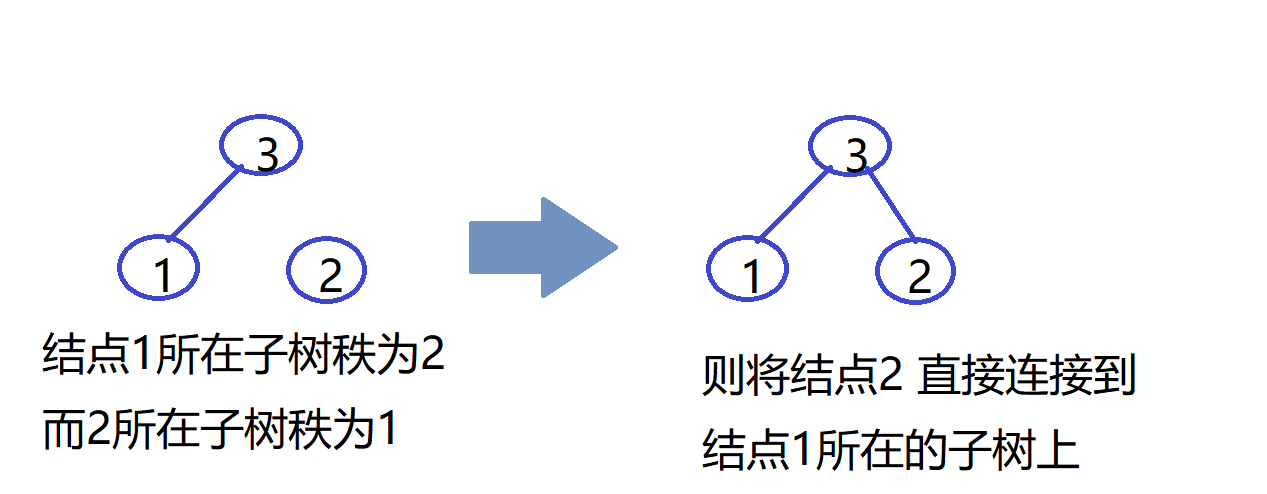
图示合并过程

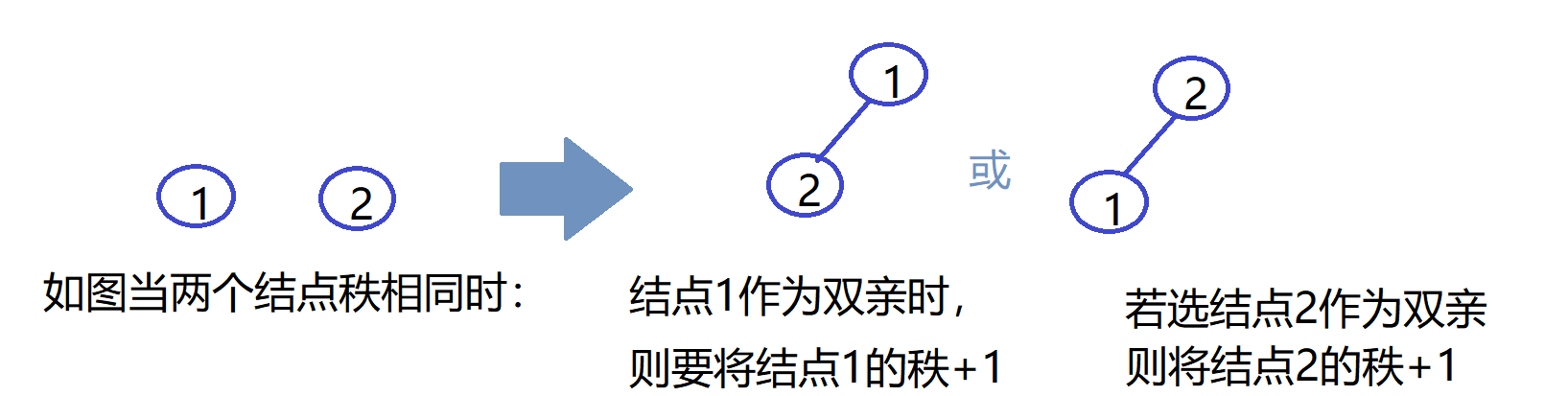
结构定义

typedef struct node
{
	int data;		//结点对应人的编号
	int rank;  //结点秩：子树的高度，合并用
	int parent;		//结点对应双亲下标
} BTree;		//并查集树的结点类型

具体代码实现

void MAKE_SET(UFSTree t[],int n )  //初始化并查集树
{
	int i;
	for (i = 1; i <= n; i++)
	{
		t[i].data = i;		//数据为该人的编号
		t[i].rank = 0;		//秩初始化为0
		t[i].parent = i;		//双亲初始化指向自已
	}
}

void UNION(UFSTree t[],int x,int y)       //将x和y所在的子树合并
{
	x = FIND_SET(t,x);	        //查找x，y分别所在分离集合树的编号
	y = FIND_SET(t,y);	       
	if (t[x].rank > t[y].rank)	        //y结点的秩小于x结点的秩
		t[y].parent = x;		        
	else			        //y结点的秩大于等于x结点的秩
	{
		t[x].parent = y;		        
		if (t[x].rank == t[y].rank)      //x和y结点的秩相同时。秩需增1
			t[y].rank++;	        
	}
}

int FIND_SET(UFSTree t[],int x)    //在x所在子树中查找集合编号
{
	if (x != t[x].parent)		                    //双亲不是自已
		return(FIND_SET(t,t[x].parent));   //递归在双亲中找x
	else
		return(x);			      //双亲是自已，返回x
}

树的应用

表达式树

• 我们会发现建成表示式的树其后序遍历正是表达式的后缀表达式，我们可以借此进行计算

伪代码

建树即计算具体实现

void InitExpTree(BTree& T, string str)//建二叉表达式树 
{
	stack<BTree> btnode;
	stack<char> op;
	int i=0;
	BTree node;

	while (str[i])
	{
		if (str[i] >= '0' && str[i] <= '9')
		{
			node = new BTNode; node->data = str[i]; node->lchild = node->rchild = NULL;
			btnode.push(node);
		}
		else if (In(str[i]))//若是运算符
		{
			if (op.empty()) op.push(str[i]);//若空直接入栈
			else
			{
				if (str[i] == ')')
				{
					while (!op.empty() && op.top() != '(')
					{
						CreateExpTree(node, NULL, btnode.top(), op.top());
						btnode.pop(); op.pop();
						node->lchild = btnode.top(); btnode.pop();
						btnode.push(node);
					}op.pop();//左括号也要出栈

				}
				else if (str[i] == '(') op.push(str[i]);
				else
				{
					if (Precede(op.top(), str[i]) == '<') op.push(str[i]); //若大于栈顶入栈
					else //弹出两个结点和运算符形成新根
					{
						while (!op.empty()&&Precede(op.top(), str[i]) != '<' )
						{
							CreateExpTree(node, NULL, btnode.top(), op.top());
							btnode.pop(); op.pop();
							node->lchild = btnode.top(); btnode.pop();
							btnode.push(node);
						}op.push(str[i]);
					}
				}
			}
		       
		}
		i++;
	}
	while (!op.empty())
	{
		CreateExpTree(node, NULL, btnode.top(), op.top());
		btnode.pop(); op.pop();
		node->lchild = btnode.top(); btnode.pop();
		btnode.push(node);
	}
	
	T = btnode.top();
}

double EvaluateExTree(BTree T)//计算表达式树
{
	double num1,num2;
	if (!T->lchild && !T->rchild)//若为操作数
	{
		return T->data - '0';
    }
	num1 = EvaluateExTree(T->lchild);
	num2 = EvaluateExTree(T->rchild);
	switch (T->data)
	{
	case '+':return num1 + num2;
	case '-':return num1 - num2;
	case '*':return num1 * num2;
	case '/':
		if (num2 == 0) 
		{
			cout << "divide 0 error!"; exit(0);
		}
		else return num1 / num2;
	default:
		break; exit(0);
	}

}

朋友圈(并查集)

伪代码

• 其他基本操作都与并查集基本操作相同

• 注意朋友圈人数，和朋友圈较大情况下，利用堆区申请
  

串

串的顺序存储结构：

定长存储:
char str[max];


堆区分配存储：
char*str;
int length;

str=new char[length];

• 链串的操作不方便较少使用

string

• find函数的使用：

1.find(str,position) 。string的find()函数用于找出字母在字符串中的位置。函数形式：
str：是要找的元素，position：字符串中的某个位置，表示从从这个位置开始的字符串中找指定元素。
可以不填第二个参数，则默认从字符串的开头进行查找。返回值为目标字符的位置，当没有找到目标字符时返回npos（打印出来为4294967295）

2.rfind()：反向查找，即rfind()是从指定位置起向前查找，直到串首。

3.find_first_of()：查找目标字符在字符串中第一次出现的位置，查找是从从位置pos起往后查找

4.find_last_of()：查找目标字符在字符串中最后一次出现位置，即查找是从pos起往前查找

5.find_first_not_of()：查找字符串中第一个与目标字符不同的字符所出现位置，即查找位置从pos起往后查找

6.find_last_not_of()：查找字符串中最后一个与目标字符不同的字符所出现位置。即查找是从位置pos起往前查找

串的BF算法（简单匹配算法）

• 从目标串的第一个字符开始和模式串的第一个字符比较，一旦不同就由目标串的第二个字符重新与模式串进行比较。

伪代码

串的KMP算法

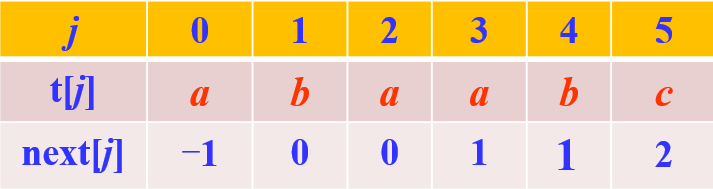
• KMP算法用next数组保存部分匹配信息：
  next[j]是指失配时，模式串下一次匹配位置

定义next[j]数组：

1.当 j=0 时，next[j] = -1

2.当 j=1 时，next[j] = 0

3.其他：当模式串t存在某个k（0＜k＜j），使得以下成立:

 “t0 t1… tk-1” = “ tj-k tj-k + 1… tj-1 ”
 **即从字符串头k个字符组成的字符串** 与 **位置j和前k-1个位置的组成字符串相同

 此时取最大k作为 next[j]

图示：求最大k

例:next[j]的对应关系

总的next数组分析，如字符串：abaabc

代码实现

void GetNext(SqString t, int next[])
{   
	int j, k;
	j = 0;  k = -1;  next[0] = -1;
	while (j < t.length - 1)
	{
		if (k == -1 || t.data[j] == t.data[k])
		{
			j++; k++;
			next[j] = k;
		}
		else  k = next[k];
}

nextval数组的引进：

对next数组的改进，多次滑动，改为直接滑到最后。

• nextval数组原则：

  t.data[j] ? = t.data[next[j])
  1.若不等，则 nextval[j] = next[j]
  2.若相等，则nextval[j] = nextval[k]

图示：

代码实现

void GetNextval(SqString t, int nextval[])	
{
	int j = 0, k = -1;
	nextval[0] = -1;
	while (j < t.length)
	{
		if (k == -1 || t.data[j] == t.data[k])
		{
			j++; k++;
			if (t.data[j] != t.data[k])
				nextval[j] = k;
			else
				nextval[j] = nextval[k];
		}
		else
			k = nextval[k];
	}
}

2.阅读代码

2.1 题目及解题代码

题目：在树的每行中找到最大值

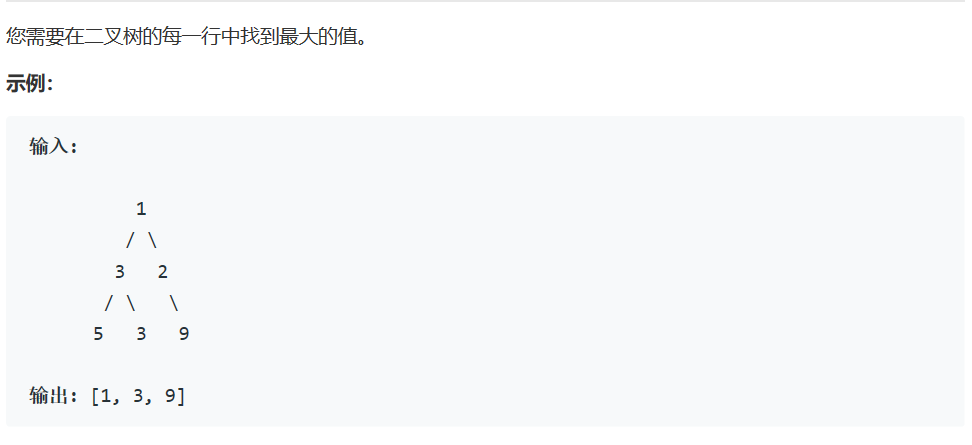
解题代码

class Solution {
public:
    vector<int> largestValues(TreeNode* root) {
        vector<int> res;

        if(root == NULL)
            return res;
        
        queue<TreeNode*> q;
        q.push(root);

        while(!q.empty()) {
            int curMax = INT_MIN;
            int size = q.size();

            for(int i=0; i<size; ++i) {
                TreeNode* node = q.front();
                q.pop();

                curMax = max(curMax, node->val);
                if(node->left)
                    q.push(node->left);
                if(node->right)
                    q.push(node->right);
            }

            res.push_back(curMax);
        }

        return res;
    }
};

2.1.1 该题的设计思路

• 该题是广度搜索树，即层次遍历（利用队列），实现遍历一层就搜索出该层最大值。

• 主要设计思路就是，在每一层层次遍历入队后，size记录该队的大小，来控制限制层之间的最大值比较。
  

2.1.2 该题的伪代码

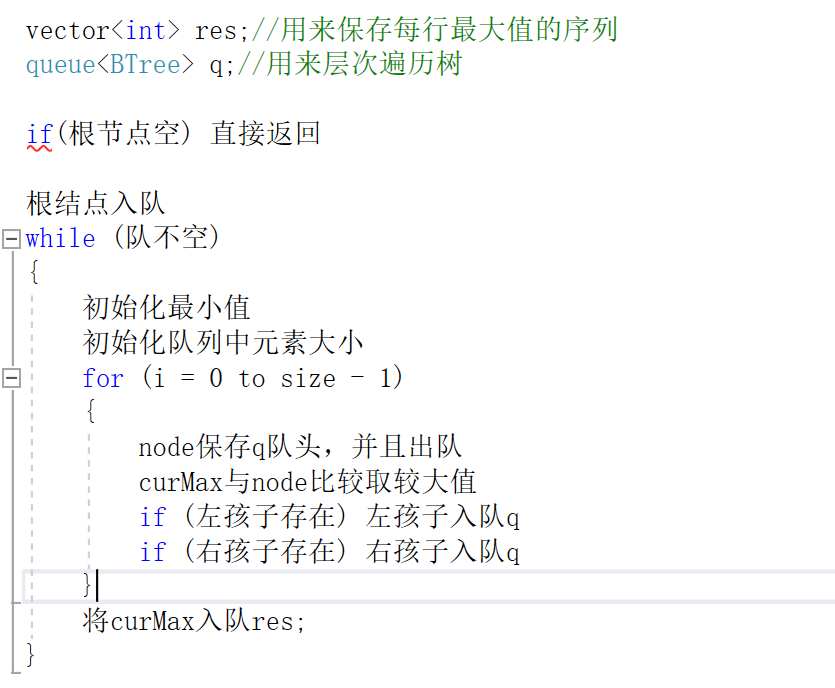
-层次遍历，出队孩子进队的操作不变，通过size值for循环来控制层之间最大值的比较，

2.1.3 运行结果

先序遍历建树 字符串：“122##5##4#3##”

建成树如下：

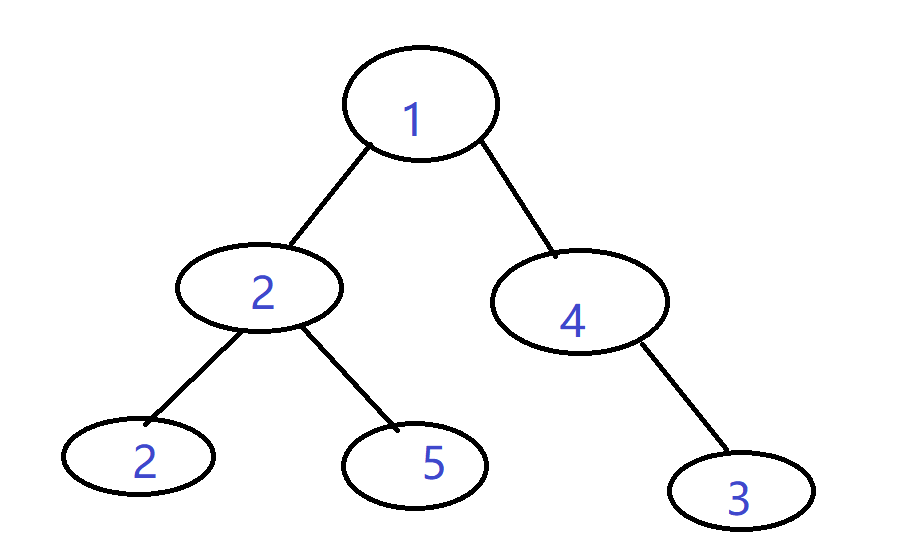
因此输出结果应为： 1 4 5

2.1.4分析该题目解题优势及难点。

• 优势：广度搜索层次遍历，一层层遍历时即比较得层得最大值，因此该题解解题思路简单

• 难点在于如何控制层之间的比较，何时最大值重新初始化进行比较。

• 若使用深度搜索利用递归的时候，要考虑该层的层数，以及每层的最大值，也是实时更新。不过对于函数设计需要思考的多一点。

• 层次遍历，时间复杂度为O（n）,利用vector序列保存，空间复杂度也O (n)

2.2题目及解题代码

题目：二叉树的后序遍历

解题代码

class Solution {//迭代解法
public:
    vector<int> postorderTraversal(TreeNode* root) {
        vector<int> res;
        stack<TreeNode*> s;
        if(root) s.push(root);
        else return res;
        while(!s.empty()){
            TreeNode* temp=s.top();
            res.push_back(temp->val);
            s.pop();
            if(temp->left) s.push(temp->left);//区别1：左孩子先入栈
            if(temp->right) s.push(temp->right);//    右孩子后入栈
        } 
        reverse(res.begin(),res.end());/区别2：结果vector需要翻转
        return res;       
    }
};

2.2.1 该题的设计思路

• 迭代法达成后序遍历。
  先序遍历的方式是根入栈，栈不空为循环条件，出栈入队，左右孩子入队，由于栈结构的特殊性，得到 根右左，进行翻转得到后序序列 左右根。

2.2.2伪代码

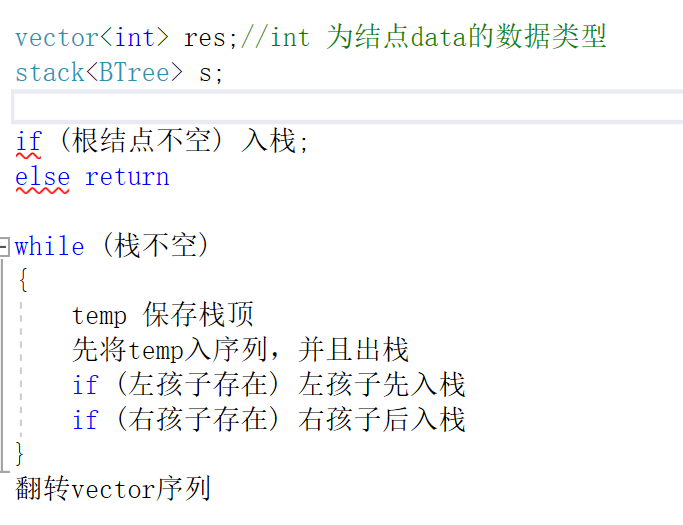
最后vector的序列即为该数后序遍历顺序

2.2.3运行结果

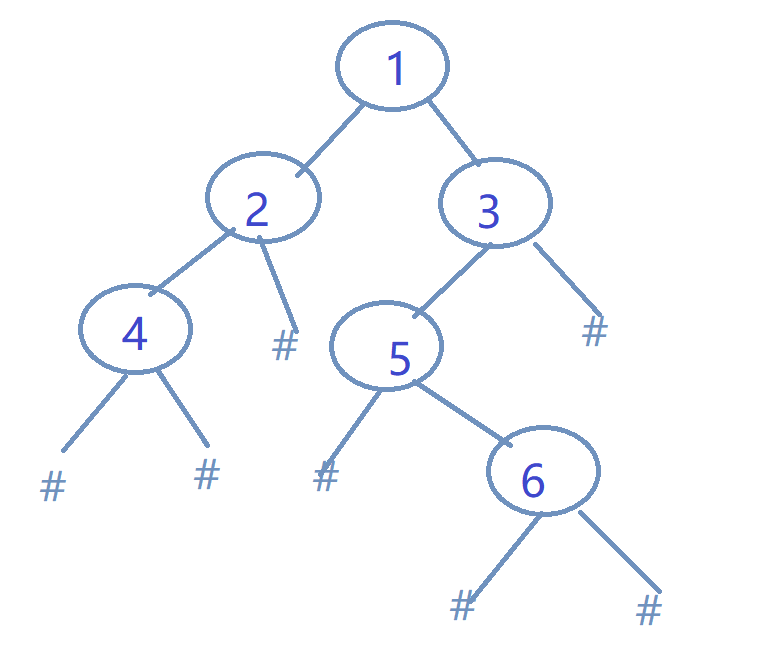
层次遍历建树，字符串为：“12345#6######”

建成树如下：

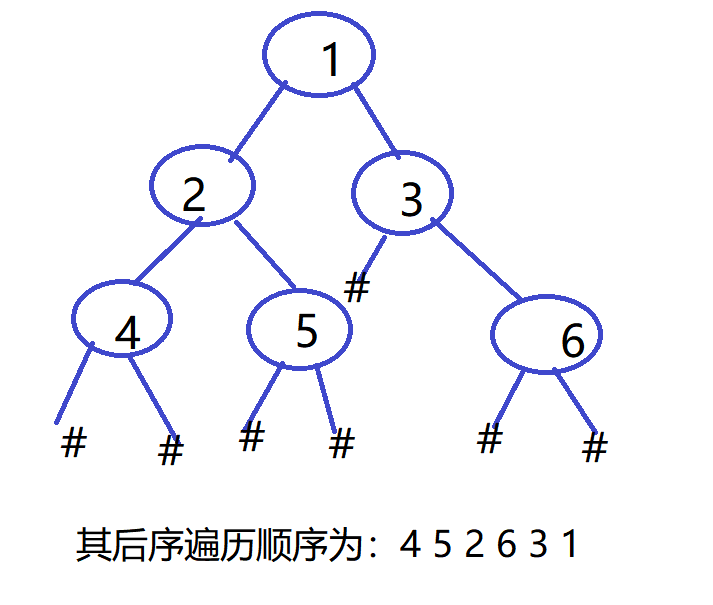
运行结果

ize

2.2.4分析该题目解题优势及难点。

• 该题难点就在于：如果用递归的话很好达成，但是要求用迭代法

• 解题优势：遍历一遍树，因此时间复杂度为O（n）,用vector保存序列，空间复杂度也为O（n）。

• 通过该题对迭代法有所了解，学习了先序序列的迭代法后进而在此基础上改造，对该题后序序列进行应用

2.3题目即解题代码

题目：

解题代码

class Solution {
public:
    TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
        return helper(nums, 0, nums.size()-1);
    }

    TreeNode* helper(vector<int>& nums, int start, int end){
        // 递归结束
        if(start > end) return nullptr;
        // 找到最大值以及索引
        int index = searchMax(nums, start, end);
        // 构造根节点
        TreeNode* root = new TreeNode(nums[index]);
        root->left = helper(nums, start, index-1); 
        root->right = helper(nums, index+1, end);
        return root;
    }

    /*
    * nums：  数组
    * start： 数组起始查找位置(闭区间)
    * end：   数组结束查找位置(闭区间)
    * return：起始到结束区间内，最大值索引
    */
    int searchMax(vector<int>& nums, int start, int end){
        int maxValue = nums[start], index = start;
        for(int i = start+1; i<=end; ++i){
            if(maxValue < nums[i]){
                maxValue = nums[i];
                index = i;
            }
        }
        return index;
    }
};

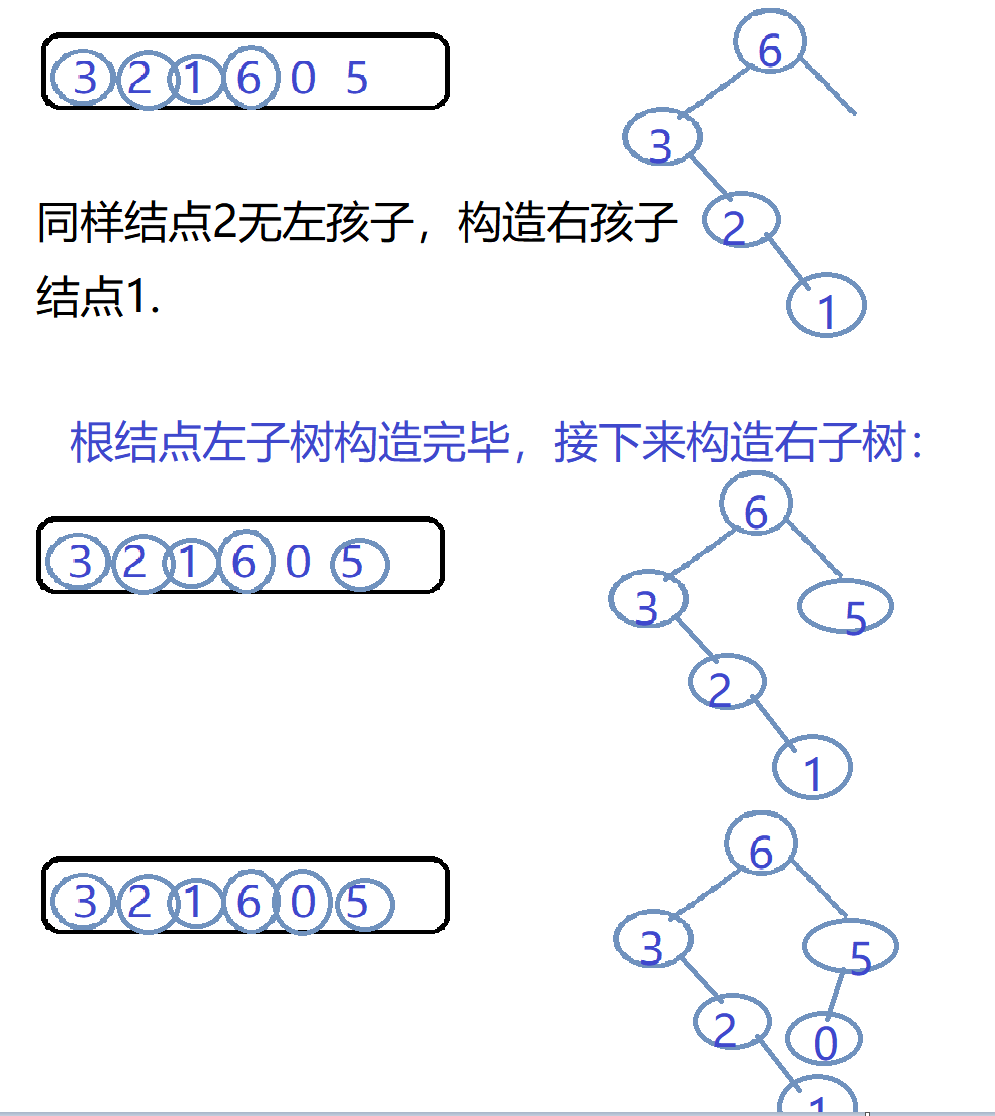
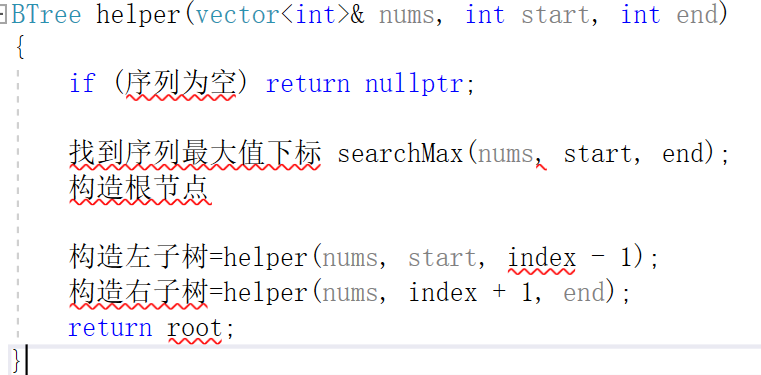
2.3.1设计思路

在序列中找到最大值，生成新结点，在分别以结点左右的序列构造该结点的左右子树

2.3.2伪代码

2.3.3运行结果

输入样例

运行结果

2.3.4分析该题目解题优势及难点。

• 优势：思路很清晰，就是根据题目要求：找出当前序列中最大值建根结点，根据最大值左右序列再分别建树。很明显采用递归的方法

• 递归类型是结点类型，最后也就是返回结点，递归建树。
  倒是和先序中序，还有中序后序建树一样，都是不断地传序列进行操作建树，不过该题倒是更为简单。

2.4题目与解题代码

题目

解题代码

class Solution {
public:
    int res = 0;
    int maxlevel = 0;
    int findBottomLeftValue(TreeNode* root) {
        helper(root, 1);
        return res;
    }

    void helper(TreeNode* root, int level){
        if(root == NULL) return;

        helper(root->left, level + 1);

        if(level > maxlevel){
            maxlevel = level;
            res = root->val;
        }

        helper(root->right, level + 1);
    }
};

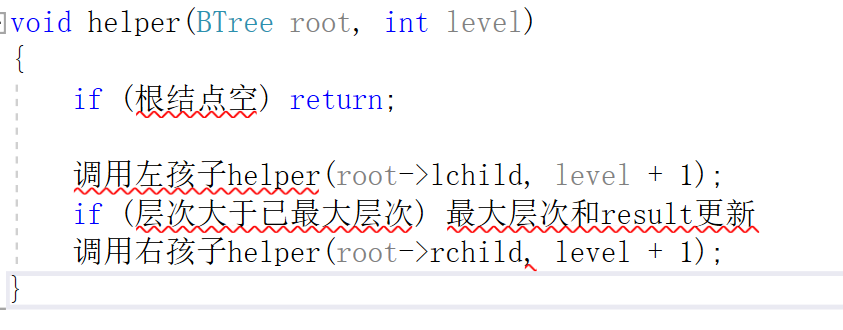
2.4.1设计思路

• 中序遍历，使用一个全局遍量记录最大深度，当到达的深度大于目前的最大深度时，为第一次到达该最大深度。之后继续更新结果，不超过该深度时，均不会更新。

图示过程

2.4.2建表达式树伪代码

2.4.3运行结果

先序序列建树：字符串“124###35#6###”

建成树应为

运行结果应为：6

2.4.4分析题目题解难点及优势

• 难点在于如何用递归达成，如何设计递归

• 解题优势：直接设全局变量来比较记录最深层，和记录数据。
  题目求得是最左角（即深度最深的左边），想想PTA中同样要求树深度有点相似。
  觉得与自己之前，将最深层变量设计在递归函数头中，用全局变量会更容易理解，递归函数内的操作写起来也简单很多

• 本题先深度最深，再要求左边。
  据此要求，作者利用全局变量不断比较更新，同时利用中序遍历，确保了在最深层次下，是左边的先被记录，因此同层的右边数据就不会被录入result。

• 中序遍历一次树 时间复杂度为O(n)，空间上用两个全局变量存储，以及递归调栈。