0.PTA得分截图

1.本周学习总结(0-5分)
1.1 总结图内容
基本概念特点
-
图分为有向图和无向图
-
若一个图中有n个顶点和e条边,每个顶点的度为di(0≤i≤n-1),则有:
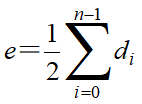
图的存储结构
邻接矩阵
-
顶点表存放顶点信息
-
邻接矩阵存放边的信息
-
特点:
邻接矩阵取边直接,因此对顶点出入度的情况也较易掌握。
邻接矩阵适合用于稠密图
结构定义
#define MAXV <最大顶点个数>
typedef struct
{ int no; //顶点编号
InfoType info; //顶点其他信息
} VertexType;
typedef struct //图的定义
{ int edges[MAXV][MAXV]; //邻接矩阵,存放边的信息
int n,e; //顶点数,边数
VertexType vexs[MAXV]; //顶点表,存放顶点信息
} MatGraph;
MatGraph g;//声明邻接矩阵存储的图
此为最基本的邻接矩阵结构定义,该邻接矩阵定义简单栈区申请,当顶点数较大时,我们需要到堆区申请。
- 注意二级指针的写法如下:

为二级指针申请完地址后,要利用循环依次为每个一级指针申请地址
以上邻接矩阵的基本结构定义中,顶点的相关信息有另外定义结构体存储信息,我们可以根据需求自行定义。
*如通常如果顶点只有编号区分,甚至直接以数字顺序为编号时,而无其他信息时,我们也可以选择像上述邻接矩阵一样,直接用一维数组表示顶点。
而经常,当边的信息不止包含长度,如带权值,带费用等其他信息时,此时我们也需要,另外定义一个结构体,来专门存储边的相关信息
- 对边另定义结构体,且无需另外的顶点信息写法参考如下:
typedef struct
{
int length;
int cost;
}edge;
typedef struct
{
int edge[MAXV][MAXV];
int n, e;
}MGraph;
- 将上述注意点结合起来,对边另定义结构体,且动态申请的方法这样写:

邻接表
基本概念特点
-
邻接表是一种顺序分配和链式分配相结合的存储结构。
(即利用数组和链表相结合) -
用数组存储每条链头结点(头结点即每个顶点),链结点存储的是边的内容(存储该顶点的邻接表或出边)。
头结点结构定义,需存储顶点信息即其后继边,保存后继关系。
链表结点保存边内容,包含该边所连终点编号,以及链的后继关系(但要注意,并非是边与边的后继关系。实际上是头结点顶点与边终点的后继关系)
利用一维数组保存头结点,称为邻接表
结构体定义
typedef struct Vnode
{ Vertex data; //顶点信息
ArcNode *firstarc; //指向第一条边
} VNode;//头结点数组
typedef struct ANode
{ int adjvex; //该边的终点编号
struct ANode *nextarc; //指向下一条边的指针
InfoType info; //该边的权值等信息
} ArcNode;//链表节点,存边内容
typedef struct
{ VNode adjlist[MAXV] ; //邻接表
int n,e; //图中顶点数n和边数e
} AdjGraph;
AdjGraph *G;//声明一个邻接表存储的图G
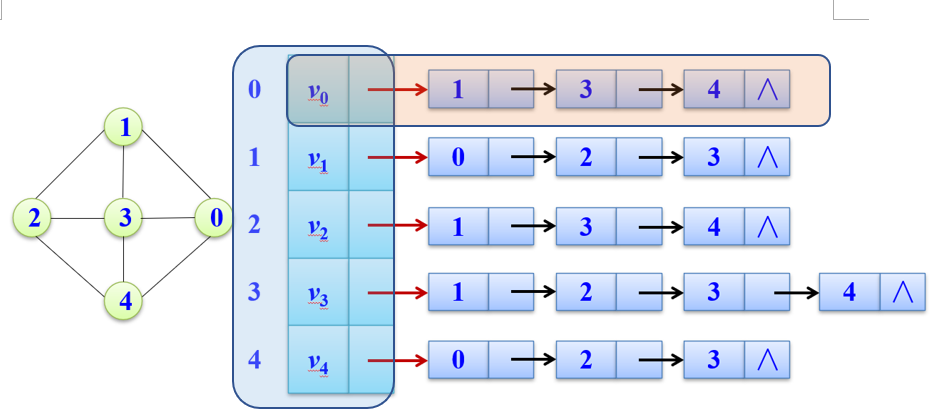
- 结合图像理解:
蓝框部分的头结点紧密相连,就如数组地址相邻
而橙框部分,则是链式结构,指针相连。
构造图
构造邻接矩阵
void CreateMGraph(MGraph& g, int n, int e)//建无向图
{
int a,b;
for (int i = 1; i <= e; i++)
{
cin >> a >> b;
g.edges[a][b] = 1;
g.edges[b][a] = 1;
}
g.e = e; g.n = n;
}
-
由代码可知

-
此邻接矩阵沿着对角线对称,因此为无向图
-
若建有向图则直接:
g.edges[a][b] = 1;
建邻接表
void CreateAdj(AdjGraph*& G, int n, int e)//创建图邻接表
{
int i, a, b;
G = new AdjGraph;
ArcNode* p;
for (i = 1; i <= n; i++)//初始化头结点都指向空
{
G->adjlist[i].firstarc = NULL;
G->adjlist[i].data = i;
}
for (i = 1; i <= e; i++)//根据输入的边
{
cin >> a >> b;
p = new ArcNode;
p->adjvex = b;
p->nextarc = G->adjlist[a].firstarc;//头插入邻接表
G->adjlist[a].firstarc = p;
p = new ArcNode;//无向图则需要双向指向
p->adjvex = a;
p->nextarc = G->adjlist[b].firstarc;
G->adjlist[b].firstarc = p;
}
G->n = n; G->e = e;
}
- 同样此为无向图,若建有向,则如注释忽略
邻接表与邻接矩阵的相互转换
图的遍历
-
概念:从图中的某个顶点开始,以某种搜索方式,对图中的其他顶点仅访问一次
-
无论是广度优先遍历还是深度优先遍历,通常使用数组visited[]来标记顶点是否被访问,通常定义成全局变量。
深度优先遍历(DFS)
-
类似迷宫问题:利用栈或者递归
-
这里我们使用递归的方法对其邻接点不断遍历。
-
遍历过程思路

邻接表的深度遍历
邻接表的深度遍历
void DFS(AdjGraph* G, int v)//v节点开始深度遍历
{
ArcNode* p;
visited[v] = 1;
cout << v;
p = G->adjlist[v].firstarc;
while (p)
{
if (visited[p->adjvex] == 0)
{
DFS(G, p->adjvex);
}
p = p->nextarc;
}
}
邻接矩阵的深度遍历
邻接矩阵的深度遍历
void DFS(MGraph g, int v)//深度遍历
{
int i;
visited[v] = 1; cout << v;
for (i = 1; i <= g.n; i++)//循环查找是否有边
{
if (visited[i]==0&&g.edges[v][i] == 1)
{
DFS(g, i);
}
}
}
- 注意由于邻接矩阵的写法:
无法知道那些边与v结点是直接相连,因此只能通过循环找点判断边是否存在,并且判断点是否被访问过
由遍历思路我们可知,我们是顺着连通的顶点不断遍历下去,因此**一旦图为非连通图,我们调用函数,就只能遍历该起点顶点所在的部分连通图**
因此特别的,考虑到图可能为非连通图的情况,我们做出以下改善:
非连通图调用过一次函数后,仍有其他点未被遍历。我们通常在**主函数中循环判断各顶点是否被遍历过,再决定是否再次调用深度遍历函数**
- 注意判断在主函数中做,DFS函数仅做连通图的深度遍历。
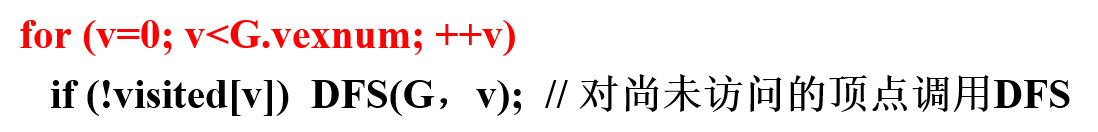
广度优先遍历(BFS)
-
同样类似迷宫问题,利用队列保存每层结点。
-
广度优先遍历思路

邻接表的广度优先遍历
邻接表的广度优先遍历
void BFS(AdjGraph* G, int v) //v节点开始广度遍历
{
queue<VNode>Q;
ArcNode* p; Vnode front;
visited[v]=1;
Q.push(G->adjlist[v]);
while (!Q.empty())
{
front = Q.front();
Q.pop();
cout << front.data ;
p = front.firstarc;
while (p!=NULL)
{
if (visited[p->adjvex] == 0)
{
Q.push(G->adjlist[p->adjvex]);
visited[p->adjvex] = 1;
}
p = p->nextarc;
}
}
}
邻接矩阵的广度优先遍历
邻接矩阵的广度优先遍历
void BFS(MGraph g, int v)//广度遍历
{
int Q[MAXV];
int f=0, r=0;//队的首尾指针
visited[v] = 1;
Q[++r] = v;//入队
while (f != r)//队不空
{
f++;
cout << Q[f];//出队
for (int i= 1; i <= g.n; i++)//同样需要循环每个顶点判断是否有边
{
if (visited[i]==0&&g.edges[Q[f]][i] == 1)//未被广度遍历过
{
visited[i] =1 ;
Q[++r] = i;//入队
}
}
}
}
- 注意邻接矩阵这里的队列,我们用了自己写的简易顺序队列:
首尾指针是: int f=0, r=0;
- 同样的与邻接表相比,无法直接知道于其有边的点,因此也是需要通过**循环查找每个点判断是否有边存在**
DFS,BFS遍历图判断图是否连通
!!多次调用函数遍历的,记得要先将visited[]数组初始化
DFS图不连通的问题已经在上面阐述过了:
我们只需在主函数中,第一次调用DFS函数后,若有出现仍未被遍历的点,则说明是非连通图。
并且只要继续调用DFS,就可做到将非连通图中的各个连通部分都分别遍历完毕。
关于BFS图是否连通问题:
判断BFS图是否连通的办法一样,一次执行后也是利用循环判断点是否全都被遍历。
但由于BFS函数并不是通DFS一样递归写法,因此也用循环判断点是否被遍历这个写法,
1.可以在BFS函数中,将所有内容都嵌套在循环内,主函数一次调用。
2.当然也可以还是一样,循环在主函数中写。
最小生成树
基本概念
-
生成树:一个连通图的生成树是一个极小连通子图,它含有图中全部n个顶点和构成一棵树的(n-1)条边。不能回路。
-
且生成树并不唯一
利用深度优先遍历,我们可以得到深度优先生成树
利用广度优先遍历,我们可以得到广度优先生成树
图示:
- 最小生成树:对于带权值的图,其中权值之和最小的生成树称为图的最小生成树。
非连通图和最小生成树(容易忽略)
- 生成树的过程一定是在一个连通图才能完成,因此非连通图必须多次调用最小生成树函数,为其多个不同连通部分生成树
- 所有连通分量的生成树组成非连通图的生成森林。
普利姆算法(Prim)
设置2个辅助数组:
1.closest[i]:最小生成树的边依附在U中顶点编号。
2.lowcost[i]表示顶点i(i ∈ V-U)到U中顶点的边权重,取最小权重的顶点k加入U。
并规定lowcost[k]=0表示这个顶点在U中
每次选出顶点k后,要队lowcost[]和closest[]数组进行修正
伪代码设计过程


具体代码
void Prim(MGraph g, int v)
{
int lowcost[MAXV], closest[MAXV];//lowcost表示到该点最短距离,closest
int i, j, k, min ;// k记录最近顶点的编号
lowcost[1] = 1;//起点最近点为它本身
for (i = 1; i <= g.n; i++) //顶点从1开始,给lowcost[]和closest[]置初值
{
lowcost[i] = g.edges[v][i];//建图时未有直接相连的边,lowcost=edges为无穷大INF
closest[i] = v;
}
for (i = 1; i < g.n; i++) //找(n-1)次剩下的顶点
{
min = INF;
for (j = 1; j <= g.n; j++) // 在(V-U)中找出离U最近的顶点k
if (lowcost[j] != 0 && lowcost[j] < min)
{
min = lowcost[j]; k = j; //
}
lowcost[k] = 0; //遍历所有点后找到距离最近点,标记k已经加入
for (j = 1; j <= g.n; j++) //修改数组lowcost和closest
if (lowcost[j] != 0 && g.edges[k][j] < lowcost[j])
{
lowcost[j] = g.edges[k][j];
closest[j] = k;
}
}
}
应用-公路村村通题目分析

1. 本题有所给数据造成不畅通情况,其实就是图不连通情况。因为选过的点我们用lowcost[]=0来表示,因此可通过遍历lowcost数组,若每个点都被选入即畅通,反之则不畅通。
2. 若不畅通根据题目要求直接输出返回,若畅通,此时我们就根据closest数组计算最低预算。因为通过closest[]数组可以知道包含全点的最短路径,closrst[]所表示的就应该是该点的前驱点
克鲁斯卡尔算法(kruscal)
- 按权值的递增次序选择合适的边来构造最小生成树的方法
- 克鲁斯卡尔算法过程:
(1)置U的初值等于V(即包含有G中的全部顶点),TE(最小生成树的边集)的初值为空集(即图T中每一个顶点都构成一个连通分量)。
(2)将图G中的边按权值从小到大的顺序依次选取:
若选取的边未使生成树T形成回路,则加入TE;
否则舍弃,直到TE中包含(n-1)条边为止。
-由于克鲁斯卡尔算法过程是对边的权重排序选边,因此我们需要另外一个存储结构来存储边的权重信息
typedef struct
{ int u; //边的起始顶点
int v; //边的终止顶点
int w; //边的权值
} Edge;
Edge E[MAXV];
- 我们利用树的并查集来解决判断是否有环路问题
具体代码实现
void Kruskal(AdjGraph *g)
{ int i,j,k,u1,v1,sn1,sn2;
UFSTree t[MAXSize];//并查集,树结构
ArcNode *p;
Edge E[MAXSize];
k=1; //e数组的下标从1开始计
for (i=0;i<g.n;i++) //由g产生的边集E
{ p=g->adjlist[i].firstarc;
while(p!=NULL)
{ E[k].u=i;E[k].v=p->adjvex;
E[k].w=p->weight;
k++; p=p->nextarc;
}
HeapSort(E,g.e); //采用堆排序对E数组按权值递增排序
MAKE_SET(t,g.n); //初始化并查集树t
k=1; //k表示当前构造生成树的第几条边,初值为1
j=1; //E中边的下标,初值为1
while (k<g.n) //生成的边数为n-1
{ u1=E[j].u;
v1=E[j].v; //取一条边的头尾顶点编号u1和v2
sn1=FIND_SET(t,u1);
sn2=FIND_SET(t,v1); //分别得到两个顶点所属的集合编号
if (sn1!=sn2) //两顶点属不同集合
{ printf(" (%d,%d):%d
",u1,v1,E[j].w);
k++; //生成边数增1
UNION(t,u1,v1);//将u1和v1两个顶点合并
}
j++; //扫描下一条边
}
}
最短路径
-
最短路径与最小生成树不:
最小生成树需要包含所有顶点, 而最短路径只考虑路径最短,
Dijkstra算法
1.从T中选取一个其距离值为最小的顶点W, 加入S
2.S中加入顶点w后,对T中顶点的距离值进行修改:
若加进W作中间顶点,从V0到Vj的距离值比不加W的路径要短,则修改此距离值;
3.重复上述步骤1,直到S中包含所有顶点,即S=V为止。
伪代码设计思路

这里我们同Prim算法建最小生成树的过程来比较看看,方便记忆:

1.Prim建成最小生成树和Dijkstra求最短路径,这两种方法的大致过程框架看起来似乎很相似。似乎都是选出最近临近点,记录选入,然后修正数组值。
2.求最短路径多了s[]数组来记录已选入的点,而生成最小树时直接由lowcost[]=0来表示已选入的点。这是由于dist[]数组最终获得的数据是源点到各点的最短距离,记录过程中不能轻易改变,而生成最小树lowcost[],是一边走一边选并且修正未选入点的距离值。因此已选入点的lowcost[]信息就可以置空来表示,而求最短路径时只能另辟数组s[]来存。
3.关于修正过程都是注意选入新点后最短路径是否发生了改变。最小生成树时,是需要边选点k边修正两个顶点集合间的最短路径,修正时只要注意选入该点后两集合间的最短路径是否改变。
而相比最短路径,最短路径中不一定包含所有的点,因此即使选入点u后,是将带选入点u的路径与当前最短路径相比较取较小。
具体代码
void Dijkstra(MGraph g, int v)//源点v到其他顶点最短路径
{
int dist[MAXV], path[MAXV],s[MAXV];
int mindistance,u;//u为每次所选最短路径点
for (int i = 0; i < g.n; i++)//初始化各数组
{
s[i] = 0;//初始已选入点置空
dist[i] = g.edges[v][i];//初始化最短路径
if (dist[i] < INF) path[i] = v;
else path[i] = -1;//即无直接到源点V的边,因此初始化为-1
}
s[v] = 1;//源点入表示已选
for (int j = 0; j < g.n; j++)//要将所有点都选入需循环n-1次
{
mindistance = INF;//每次选之前重置最短路径
for (int i = 1; i < g.n; i++)//每次都遍历源点以外其他点来选入点
{
if (s[i] == 0 && dist[i] < mindistance)//在未选的点中找到最短路径
{
mindistance = dist[i];
u = i;//u记录选入点
}
}
s[u] = 1;//最后记录的u才为最后选入点
for (int i = 1; i < g.n; i++)//修正数组值
{
if (s[i] == 0)//!!仅需修改未被选入点的,已选入的既定
{
if (g.edges[u][i] < INF && dist[u] + g.edges[u][i] < dist[i])//先判断选入点到与该点存在时再比较判断
{
dist[i] = dist[u] + g.edges[u][i];
path[i] = u;
}
}
}
}
Dispath(dist, path, s, g.n, v);
}
Dijkstra算法特点:
1.不适用带负权值的带权图求单源最短路径。
2. 不适用求最长路径长度:
最短路径长度是递增
顶点u加入S后,不会再修改源点v到u的最短路径长度
(按Dijkstra算法,找第一个距离源点S最远的点A,这个距离在以后就不会改变。但A与S的最远距离一般不是直连。)
Floyd算法
- 该算法思路较简单:
就是不断将每个顶点都加入的过程中,同时不断更新最短路径矩阵**
算法思路
- 有向图G=(V,E)采用邻接矩阵存储
- 二维数组A用于存放当前顶点之间的最短路径长度,分量A[i][j]表示当前顶点i到顶点j的最短路径长度。
- 递推产生一个矩阵序列A0,A1,…,Ak,…,An-1
Ak+1[i][j]表示从顶点i到顶点j的路径上所经过的顶点编号k+1的最短路径长度。
具体代码
void Floyd(MatGraph g) //求每对顶点之间的最短路径
{
int A[MAXVEX][MAXVEX]; //建立A数组
int path[MAXVEX][MAXVEX]; //建立path数组
int i, j, k;
for (i = 0; i < g.n; i++)
for (j = 0; j < g.n; j++)
{
A[i][j] = g.edges[i][j];
if (i != j && g.edges[i][j] < INF)
path[i][j] = i; //i和j顶点之间有一条边时
else //i和j顶点之间没有一条边时
path[i][j] = -1;
}
for (k = 0; k < g.n; k++) //求Ak[i][j]
{
for (i = 0; i < g.n; i++)
for (j = 0; j < g.n; j++)
if (A[i][j] > A[i][k] + A[k][j]) //找到更短路径
{
A[i][j] = A[i][k] + A[k][j]; //修改路径长度
path[i][j] = k; //修改经过顶点k
}
}
}
拓扑排序及关键路径
拓扑排序基本概念特点
-
拓扑序列:在一个有向图中找一个拓扑序列的过程称为拓扑排序。
-
序列必须满足条件:
每个顶点出现且只出现一次。
若存在一条从顶点 A 到顶点 B 的路径,那么在序列中顶点 A 出现在顶点 B 的前面。 -
拓扑排序:在一个有向无环图中找一个拓扑序列的过程称为拓扑排序。
注意必须是有向无环图
排序过程
- 1.从有向图中选取一个没有前驱的顶点,并输出之;
- 2.从有向图中删去此顶点以及所有以它为尾的弧;
- 3.重复上述两步,直至图空,或者图不空但找不到无前驱的顶点为止。
根据此排序规则,我们对下图进行拓扑排序

得到的拓扑序列为:C1--C2--C3--C4--C5--C7--C9--C10--C11--C6--C12--C8
或: C9--C10--C11--C6--C1--C12--C4--C2--C3--C5--C7--C8
由此可知,拓扑序列并未是唯一的
伪代码

- 需注意的是,我们不仅可以栈结构来保存要删除的前驱点,我们**同样可以使用队列**
- 但正是**由于栈和队列出入方式的不同**,所以同一个有向图,我们得到的可能就是不同的拓扑序列
具体代码
void TopSort(AdjGraph* G)//邻接表拓扑排序
{
ArcNode* p;
int stack[MAXV], top=-1;//顺序栈结构
int visitedcout = 0;//记录已得到的拓扑序列长度
int sequence[MAXV];//用于保存拓扑序列
for (int i = 0; i < G->n; i++)
{
G->adjlist[i].count = 0;
}
for (int i = 0; i < G->n; i++)//遍历每条链,记录每个节点的入度
{
p = G->adjlist[i].firstarc;
while (p)
{
G->adjlist[p->adjvex].count++;
p = p->nextarc;
}
}
for (int i = 0; i < G->n; i++)//先遍历图顶点,找出入度为0的点入栈
{
if (G->adjlist[i].count == 0)
{
top++; stack[top] = i;
}
}
int i = 0;
while (top!=-1)//接下来通过不断出栈过程中同时判断是否有点要入栈
{
sequence[i] = stack[top]; visitedcout++;//保存拓扑序列,并且记录已遍历点
p = G->adjlist[stack[top]].firstarc;//则该点的后继点入度都要减一
top--;//出栈
while (p)
{
G->adjlist[p->adjvex].count--;
if (G->adjlist[p->adjvex].count == 0)
{
top++; stack[top] = p->adjvex;
}
p = p->nextarc;
}
i++;
}
if (visitedcout == G->n)//则无环路得到拓扑序列,
{
cout << sequence[0];
for (int i = 1; i < G->n; i++)
{
cout << " " << sequence[i];
}
}
else cout << "error!";
}
关于如何判断图是否存在有环
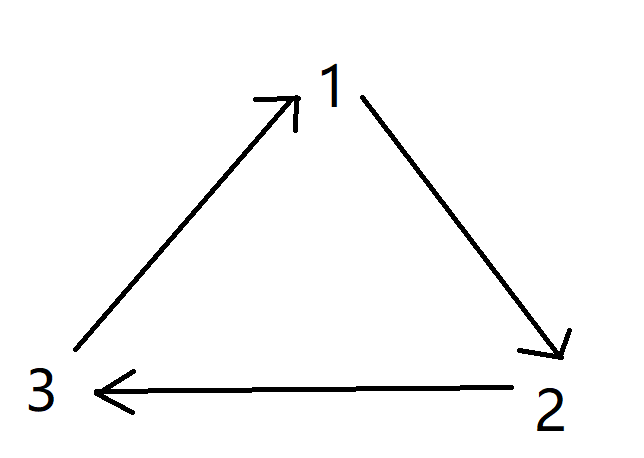
- 举最简单的例子,由上图可知,在一个环路中,我们是没办法找到入度为0的顶点。
同样的全局图来说,即使利用拓扑排序可以得到一定的拓扑序列,但只要存在环路,就不可能得到完整的拓扑序列
- 因此判断是否存在有环,只需记录一下得到的序列长度,与图的顶点数相比即可知,序列是否完整,是否就是拓扑序列
- 具体实现也已经在上述具体代码中体现
关键路径基本概念
- AOE-网(Activity ON Edge Network):
用顶点表示事件,用有向边e表示活动,边的权c(e)表示活动持续时间。是带权的有向无环图
整个工程完成的时间为:从有向图的源点到汇点的最长路径。又叫关键路径
如何求关键事件和关键路径
求关键事件
事件v最早开始时间ve(v):v作为源点事件最早开始时间为0。
由于v为源点事件最早开始时间一定是前驱事件已完成。因此:
当v为初始源点时: ve(v)=0
其余:ve(v)=MAX{ve(x)+a,ve(y)+b,ve(z)+c}
事件v的最迟开始时间vl(v):定义在不影响整个工程进度的前提下,事件v必须发生的时间称为v的最迟开始时间
由于最迟时间要保证后继事件能完成,因此取最小
当v为终点时:vl(v)=ve(v)
其他 vl(v)=MIN{vl(x)-a,vl(y)-b,vl(z)-c}
- 关键路径点:ve=vl
注意:计算:ve(i)最早开始和vl(i)最迟开始必须在拓扑有序和逆拓扑有序计算。
活动:边的最早开始时间和最迟开始时间
1.活动a(边)的最早开始时间e(a)指该活动起点x事件的最早开始时间e(a)=ve(x)
2.活动a的最迟开始时间l(a)指该活动终点y事件的最迟开始时间与该活动所需时间之差
l(a)=vl(y)-c
- 关键活动:d(a)=l(a)-e(a),若d(a)为0,则称活动a为关键活动。
求关键路径

1.2.谈谈你对图的认识及学习体会。
-
图的应用感觉比之前学的结构更加广了,实际应用在地图啊什么的比较多,好比村村通应用最小生成树问题,最短路径问题,还有关键路径。
-
练习编程的题目,感觉其实思路都是比较直接,实质明显,最小生成树问题啊,最短路径问题。
后面做阅读代码部分的时候,有一些题目的时候都是没什么思路,看了解法,才发现其实是所学知识的变化、延展。比如下面阅读代码的无向图的“拓扑”,所以阅读时候也对思路进行认真分析 -
还有一个感觉就是图部分的编程对前面所学知识应用的更多,结合的内容更多,对编程能力更有考验。前面学习完栈和队列后对STL库的应用就会比较多,然后在这次复习题的代码中也会经常发现,
对于一些简单的变量类型和简单的处理,有的时候我们自己写顺序栈,顺序队的其实也很简单。还有啊比如Kruscal算法的代码利用并查集,这就是并查集的应用结合。 -
学习体会:一开始学图,对于图的存储结构,邻接矩阵和邻接表,相比起树的存储结构,感觉其实更好理解。还有图的遍历,深度优先,广度优先遍历,在前面树已学的基础下,对这部分内容感觉更加得心应 手。但是后面关于最小生成树,最短路径,以及拓扑序列集关键路径,这三部分内容,自己预习的时候就是明显感觉到,有点难理解,然后经过课上老师讲解后理解了算法的执行过程后,最后主要的压力还是得要自己去编写,去细细品代码的具体细节。
2.阅读代码
2.1 题目及解题代码
题目:最小高度树

解题代码
class Solution {
public:
vector<int> findMinHeightTrees(int n, vector<vector<int>>& edges) {
vector<int> indegree(n);//入度数组
vector<vector<int>> graph(n);//图形表示
vector<int> result;
for (int i = 0; i < n; i++)
{
indegree[i] = 0;//初始化入度序列为0
graph.push_back(v);
}
for (int i = 0; i < edges.size(); i++)//构造图与入度数组:无向图,两个点都要处理
{
graph[edges[i][0]].push_back(edges[i][1]);
graph[edges[i][1]].push_back(edges[i][0]);
indegree[edges[i][0]]++;
indegree[edges[i][1]]++;
}
queue<int> myqueue;//装载入度为1的queue
for (int i = 0; i < n; i++)
{
if (indegree[i] == 1)
myqueue.push(i);
}
int cnt = myqueue.size();//!!令cnt等于myqueue.size(),一次性将入度为1的点全部删去。
while (n>2)
{
n -= cnt;//一次性将入度为一的点全部删去!!不能一个一个删!
while (cnt--)
{
int temp = myqueue.front();
myqueue.pop();
indegree[temp] = 0;
//更新temp的邻接点:若temp临接点的入度为1,则将其放入queue中。
for (int i = 0; i < graph[temp].size(); i++)
{
if (indegree[graph[temp][i]] != 0)
{
indegree[graph[temp][i]]--;
if (indegree[graph[temp][i]] == 1)//放在这里做!只判断邻接点。
myqueue.push(graph[temp][i]);
}
}
}
cnt = myqueue.size();
}
while (!myqueue.empty())
{
result.push_back(myqueue.front());
myqueue.pop();
}
return result;
}
};
2.1.1 该题的设计思路

1.删除入度为1的点
有向图的拓扑序列时,我们删除的是前驱为0的节点。
而对于无向图,由于无向图是双向,入度为1即可说明该点就是**图的边缘点**
2.关于一次性删除的问题
当我们按照有向图的拓扑序列一个个删除点并同时判断是否入队时
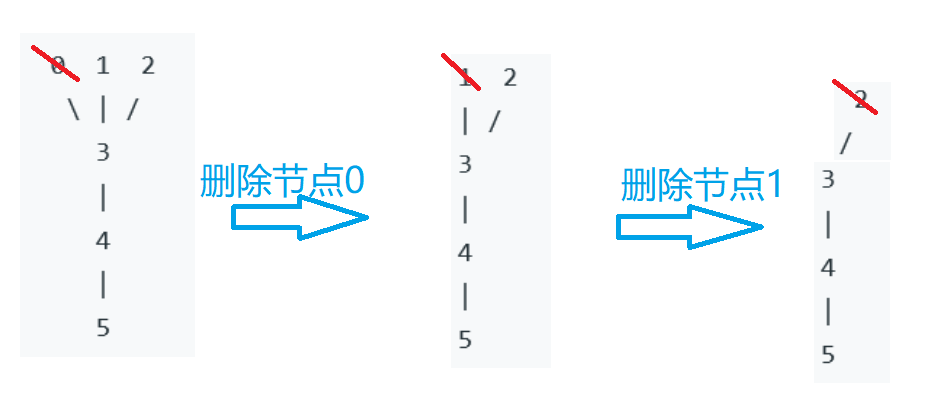

而当我们采用我们一次性删除的思路时;

解释说明:
- 由题意可知,根据几何想象,这其实就是一个图不断缩小的过程,即**不断地把边缘顶点删除,最终得到中间的根节点的过程**
- 对于该无向图来理解,当我们不断删减边缘点时,也在不断改变图,改变顶点入度,所以**每删除一个点,图的中心节点也可能发生了变化**
- 因此控制一次性删除,我们其实可以理解成,**一圈圈删减,这才叫缩小,所有方向的边缘点都同时删除,才能达到中心节点不偏移**
2.1.2 该题的伪代码

2.1.3 运行结果
示例1:


示例2:

2.1.4分析该题目解题优势及难点。
-
题目难点:其实一开始看该题目的时候,毫无思路,感觉要获得图中心节点,用遍历什么的都很难想到什么思路,所以我觉得该题难点就是思路难。
-
解题优势:正是因为对题目思路毫无头绪,所以对该题的解题思路感到很新奇-拓扑序列的变式
从有向无环图的拓扑序列,延展到无向图。
虽然主要目的并不是为了得到无向图的该序列,但也是按照该思路的过程,不断删除点缩图。 -
该思路无向图的拓扑,将各顶点都遍历了一遍,所以时间复杂度应为O(n).
-
但是同样无向图的该拓扑方式前提同样也是无环路,而题目给的样例也符合该条件:本题名为最小高度树
且
2.2题目及解题代码
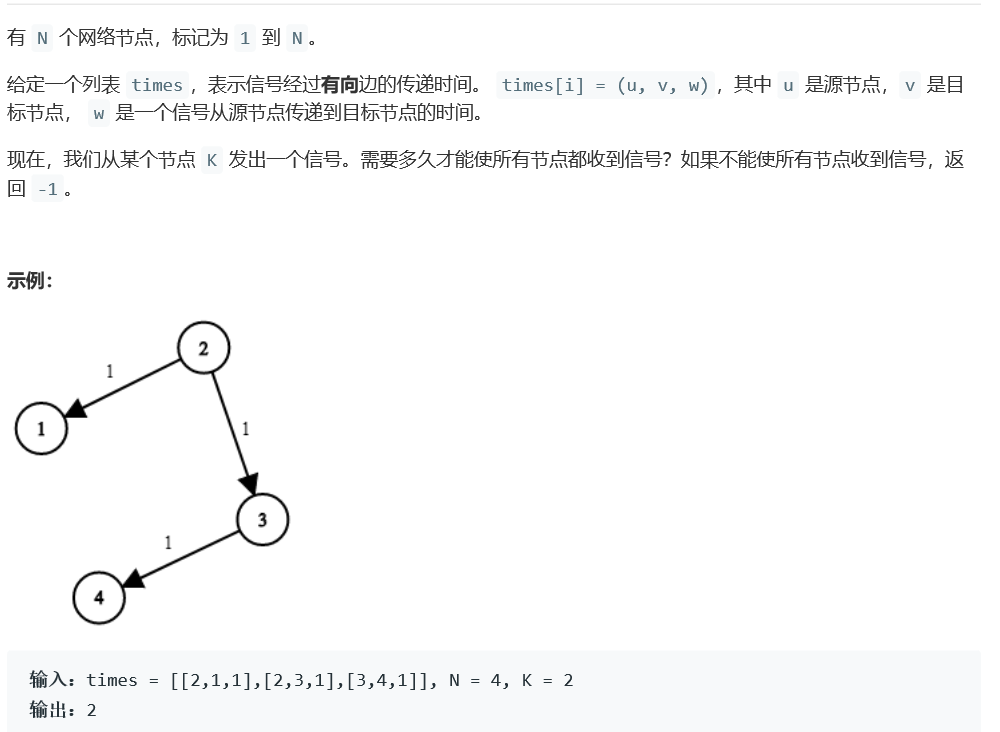
题目:网络延迟时间
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
const int INF = 0x3f3f3f3f;
vector<int> dist(N+1, INF); // 保存到起点的距离
vector<bool> st(N+1, false); // 是否最短
typedef pair<int, int> PII;
unordered_map<int, vector<PII>> edges; // 邻接表
queue<int> q;
q.push(K);
dist[K] = 0;
st[K] = true; // 是否在队列中
for (auto &t: times){
edges[t[0]].push_back({t[1], t[2]});
}
while (!q.empty()){ // 当没有点可以更新的时候,说明得到最短路
auto t = q.front();
q.pop();
st[t] = false;
for (auto &e: edges[t]){ // 更新队列中的点出发的 所有边
int v = e.first, w = e.second;
if (dist[v] > dist[t] + w){
dist[v] = dist[t] + w;
if (!st[v]){
q.push(v);
st[v] = true;
}
}
}
}
int ans = *max_element(dist.begin()+1, dist.end());
return ans == INF ? -1: ans;
}
};
2.2.1设计思路
-
这道题其实就是求出点到各顶点的最短路径,求出点K到其他各点的最短距离后,再找出其中的最大距离
-
在题解中,关于最短路径解法有DisjKstra,Floyd,SPFA。由此对SPFA该种算法进行学习:
SPFA算法实现方法:
- 建立一个队列,初始时队列里只有起始点
- 在建立一个表格记录起始点到所有点的最短路径(该表格的初始值要赋为极大值,该点到他本身的路径赋为0)。
- 然后执行松弛操作(更新数据),用队列里有的点去刷新起始点到所有点的最短路,**如果刷新成功且被刷新点不在队列中则把该点加入到队列最后。重复执行直到队列为空。**
2.2.2伪代码
SPFA算法

2.2.3运行结果

2.2.4题目难点及解题优势
-
题目难点:一个就是对题目的理解。
网络信号需要多久才能使所有节点都收到信息,到达每一个顶点时间应当都是以到该点的最短路径来记
而使所有节点都能接收到信息,则是所有顶点中,最晚收到,即该点的最短路径最长的。 -
算法优点:
通常可用于求含负权边的单源最短路径(DisjKstra权重是一定不能为负的)
以及判负权环(如果一个点进入队列达到n次,则表明图中存在负环,没有最短路径。) -
SPFA算法期望的时间复杂度:O(ke), 其中k为所有顶点进队的平均次数,可以证明k一般小于等于2。
2.3题目及解题代码
题目

解题代码
class Solution {
public:
int findTheCity(int n, vector <vector<int>> &edges, int distanceThreshold) {
// 定义二维D向量,并初始化各个城市间距离为INT_MAX(无穷)
vector <vector<int>> D(n, vector<int>(n, INT_MAX));
// 根据edges[][]初始化D[][]
for (auto &e : edges) {
// 无向图两个城市间的两个方向距离相同
D[e[0]][e[1]] = e[2];
D[e[1]][e[0]] = e[2];
}
// Floyd算法
for (int k = 0; k < n; k++) {
// n个顶点依次作为插入点
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (i == j || D[i][k] == INT_MAX || D[k][j] == INT_MAX) {
// 这些情况都不符合下一行的if条件,
// 单独拿出来只是为了防止两个INT_MAX相加导致溢出
continue;
}
D[i][j] = min(D[i][k] + D[k][j], D[i][j]);
}
}
}
// 选择出能到达其它城市最少的城市ret
int ret;
int minNum = INT_MAX;
for (int i = 0; i < n; i++) {
int cnt = 0;
for (int j = 0; j < n; j++) {
if (i != j && D[i][j] <= distanceThreshold) {
cnt++;
}
}
if (cnt <= minNum) {
minNum = cnt;
ret = i;
}
}
return ret;
}
};
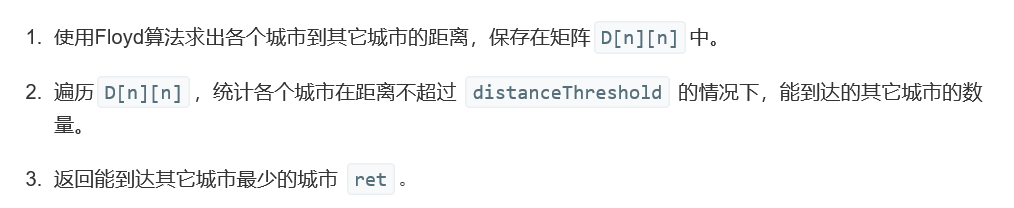
2.3.1设计思路
-
该题其实还是对最短路径的应用,之所以采用floyd算法,是因为将各个城市间最短路径存在矩阵中,这样存储数据更加方便比较
-
之后利用矩阵中的数据进行比较,求出各个城市的邻城市即可,就可以找到最少的城市
2.3.2伪代码

2.3.3运行结果
示例1:
示例2:

2.3.4题目难点及解题优势
-
该题解题思路较简单,通过Floyd算法就可得到各个城市间的最短距离,统计一下即可得到各个城市在规定范围的城市数。
-
Floyd算法,一层循环控制每个点的选入,另外两层循环控制矩阵的更新,因此三层循环时间复杂度O(n^3)
-
不过忽然想到,要获取顶点在一定距离范围内的邻居点,其实就有点像PTA上的六度空间那道题目。
六度空间是求各点距离不超过6的点所占总点百分比。我当时写的是用广度遍历。
不过区别貌似在于,六度空间顶点间的边不带距离值,所以用广度也不算太麻烦,所以如果用Floyd算法解六度空间应该也是完全可以的,但边带值的这题使用广度遍历可能一些操作上还是有点麻烦