作者:
晚于: 2020-08-12 12:00:00后提交分数乘系数50%
截止日期: 2020-08-19 12:00:00
问题描述 :
给你一棵以 root 为根的 二叉树 (注意:不一定是二叉搜索树),请你返回任意二叉搜索子树的最大键值和。
二叉搜索树的定义如下:
任意节点的左子树中的键值都 小于 此节点的键值。
任意节点的右子树中的键值都 大于 此节点的键值。
任意节点的左子树和右子树都是二叉搜索树。
示例 1:
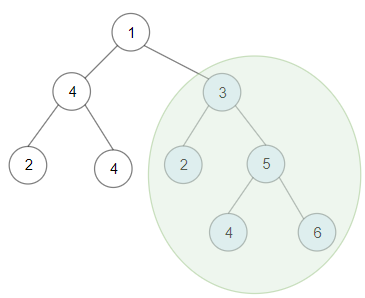
输入:root = [1,4,3,2,4,2,5,null,null,null,null,null,null,4,6]
输出:20
解释:因为以1为根的二叉树不是二叉搜索树,所以键值为 3 的子树是和最大的二叉搜索树。
示例 2:
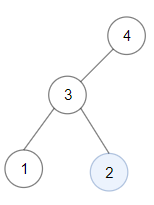
输入:root = [4,3,null,1,2]
输出:2
解释:因为以3或4为根的二叉树不是二叉搜索树,所以键值为 2 的单节点子树是和最大的二叉搜索树。
示例 3:
输入:root = [-4,-2,-5]
输出:0
解释:所有节点键值都为负数,和最大的二叉搜索树为空。
示例 4:
输入:root = [2,1,3]
输出:6
示例 5:
输入:root = [5,4,8,3,null,6,3]
输出:7
说明:
每棵树最多有 20000 个节点。
每个节点的键值在 [-10^4 , 10^4] 之间。
可使用以下main函数:
#include <iostream>
#include <queue>
#include <stack>
#include<cstdlib>
#include <climits>
#include <cstring>
#include<map>
using namespace std;
struct TreeNode
{
int val;
TreeNode *left;
TreeNode *right;
TreeNode() : val(0), left(NULL), right(NULL) {}
TreeNode(int x) : val(x), left(NULL), right(NULL) {}
TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
};
TreeNode* inputTree()
{
int n,count=0;
char item[100];
cin>>n;
if (n==0)
return NULL;
cin>>item;
TreeNode* root = new TreeNode(atoi(item));
count++;
queue<TreeNode*> nodeQueue;
nodeQueue.push(root);
while (count<n)
{
TreeNode* node = nodeQueue.front();
nodeQueue.pop();
cin>>item;
count++;
if (strcmp(item,"null")!=0)
{
int leftNumber = atoi(item);
node->left = new TreeNode(leftNumber);
nodeQueue.push(node->left);
}
if (count==n)
break;
cin>>item;
count++;
if (strcmp(item,"null")!=0)
{
int rightNumber = atoi(item);
node->right = new TreeNode(rightNumber);
nodeQueue.push(node->right);
}
}
return root;
}
int main()
{
TreeNode* root;
root=inputTree();
int res=Solution().maxSumBST(root);
cout<<res;
}
输入说明 :
首先输入结点的数目n(注意,这里的结点包括题中的null空结点,所以这里的n可能超过20000)
然后输入n个结点的数据,需要填充为空的结点,输入null。
输出说明 :
输出一个整数
输入范例 :
输出范例 :
#include <iostream> #include <queue> #include <stack> #include<cstdlib> #include <climits> #include <cstring> #include<map> using namespace std; struct TreeNode { int val; TreeNode *left; TreeNode *right; TreeNode() : val(0), left(NULL), right(NULL) {} TreeNode(int x) : val(x), left(NULL), right(NULL) {} TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {} }; class Solution { public: int max_sum = INT_MIN; int maxSumBST(TreeNode* root) { dfs(root); return max(0,max_sum); } //数组返回的顺序为是否二叉搜索树,最大和,最大值,最小值 vector<int> dfs(TreeNode* root) { if(root==NULL) return {1,0,INT_MIN,INT_MAX}; vector<int> left=dfs(root->left); vector<int> right=dfs(root->right); if(!left[0]||!right[0]||left[2]>=root->val||right[3]<=root->val) return {0,-1,-1,-1};//非二叉搜索树的时候后面三个随意取 max_sum=max(max_sum,left[1]+right[1]+root->val); right[2]=right[2]==INT_MIN?root->val:right[2]; left[3]=left[3]==INT_MAX?root->val:left[3]; return {1,left[1]+right[1]+root->val,right[2],left[3]}; } }; TreeNode* inputTree() { int n,count=0; char item[100]; cin>>n; if (n==0) return NULL; cin>>item; TreeNode* root = new TreeNode(atoi(item)); count++; queue<TreeNode*> nodeQueue; nodeQueue.push(root); while (count<n) { TreeNode* node = nodeQueue.front(); nodeQueue.pop(); cin>>item; count++; if (strcmp(item,"null")!=0) { int leftNumber = atoi(item); node->left = new TreeNode(leftNumber); nodeQueue.push(node->left); } if (count==n) break; cin>>item; count++; if (strcmp(item,"null")!=0) { int rightNumber = atoi(item); node->right = new TreeNode(rightNumber); nodeQueue.push(node->right); } } return root; } int main() { TreeNode* root; root=inputTree(); int res=Solution().maxSumBST(root); cout<<res; }