慕课(视频)pku的dfs例子实现
#include<iostream>
#include<cstdio>
#include<cstring>
using namespace std;
int path[11];
int arr[11][11];
bool tag[11];
#define endl ' '
/*
dfs的四个步骤
1、定义dfs的功能
2、if() 结束条件
3、写一个for(遍历所有子节点)
4、return dfs的结果
*/
bool dfs1(int v,int end,int& depth) //输出其中一条路径,但是这样没有遍历所有的点,所以不算是完整的dfs
{
if(v==end)
{
path[depth]=v;
depth++; //注意先赋值再++
return true;
}
if(tag[v]==false) return false;
tag[v]=false;
path[depth]=v;
depth++;
for(int i=1;i<11;i++)
{
if(arr[v][i]==1 && dfs1(i,end,depth))
return true;
}
depth--;
return false;
}
void dfs2(int v,int end,int depth)
{
if(v==end)
{
path[depth]=v;
for(int i=0;i<=depth;i++)
printf("%d ",path[i]);
printf(" ");
return;
}
if(tag[v]==false) return;
tag[v]=false;
path[depth]=v;
for(int i=1;i<11;i++)
{
if(arr[v][i]==1)
dfs2(i,end,depth+1);
}
tag[v]=true;
}
int main()
{
memset(arr,0,sizeof(arr)); //在cstring库里,把数组全部初始化为0
arr[1][2]=arr[1][3]=1;
arr[2][1]=arr[2][4]=1;
arr[3][1]=arr[3][4]=arr[3][5]=arr[3][7]=1;
arr[4][2]=arr[4][3]=arr[4][5]=arr[4][8]=1;
arr[5][3]=arr[5][4]=arr[5][6]=1;
arr[6][5]=arr[6][8]=1;
arr[7][3]=arr[7][9]=arr[7][10]=1;
arr[8][4]=arr[8][6]=1;
arr[9][7]=arr[10][7]=1;
//bool tag[11]注意在全局里面定义了,这边再定义一次。初始化是针对这边的数组,但是函数中用的是全局的
//这样就会出现逻辑错误
memset(tag,1,sizeof(tag));
int num=0;
int& depth=num;
int begin=1;
int end=8;
printf("全部路径: ");
dfs2(begin,end,0);
printf("输出其中一条路径 ");
if(dfs1(begin,end,depth))
{
for(int i=0;i<depth;i++)
printf("%d ",path[i]);
printf(" ");
}
return 0;
}
执行结果如下:
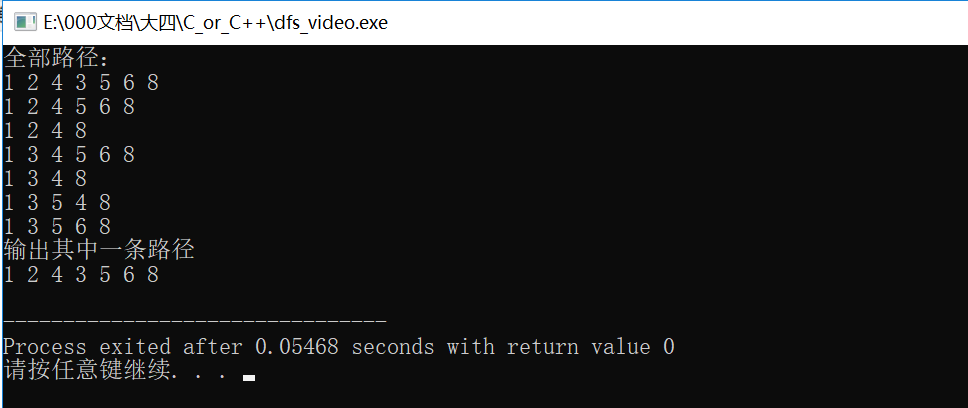
leetcode104
树是图的一种,只是他是只有左右节点(即只有两个子节点的图)
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution
{
public:
//法一,由下向上
int dfs1(TreeNode* root)
{
if(root->left==NULL && root->right==NULL)
return 1;
int left_len,right_len;
if(root->left) left_len=dfs(root->left); //注意左or右节点为空的时候。
else left_len=0;
if(root->right) right_len=dfs(root->right);
else right_len=0;
return (max(left_len,right_len)+1);
}
//法二 由上而下
void dfs2(TreeNode* root,int depth,int& max_depth)
{
if(root->left==NULL && root->right==NULL)
max_depth=max(depth,max_depth);
if(root->left)
dfs(root->left,depth+1,max_depth);
if(root->right)
dfs(root->right,depth+1,max_depth);
}
int maxDepth(TreeNode* root)
{
if(!root) //注意空树的时候
return 0;
int ans=0;
int& max_depth=ans; //不能用全局函数的话,可以用引用代替
dfs2(root,1,max_depth); //depth初始化为1
return max_depth;
}
};
//一个空树 左右节点不全在的时候