如果有两个变量:X、Y,最终计算出的相关系数的含义可以有如下理解:
(1)、当相关系数为0时,X和Y两变量无关系。
(2)、当X的值增大(减小),Y值增大(减小),两个变量为正相关,相关系数在0.00与1.00之间。
(3)、当X的值增大(减小),Y值减小(增大),两个变量为负相关,相关系数在-1.00与0.00之间。
相关系数的绝对值越大,相关性越强,相关系数越接近于1或-1,相关度越强,相关系数越接近于0,相关度越弱。
通常情况下通过以下取值范围判断变量的相关强度:相关系数
0.8-1.0 极强相关
0.6-0.8 强相关
0.4-0.6 中等程度相关
0.2-0.4 弱相关
0.0-0.2 极弱相关或无相关
皮尔逊相关
在统计学中,皮尔逊积矩相关系数(英语:Pearson product-moment correlation coefficient,又称作 PPMCC或PCCs[1], 文章中常用r或Pearson's r表示)
也称为积差相关(或积矩相关)是英国统计学家皮尔逊于20世纪提出的一种计算直线相关的方法。
假设有两个变量X、Y,那么两变量间的皮尔逊相关系数可通过以下公式计算:


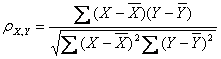

function coeff = myPearson(X , Y) % 本函数实现了皮尔逊相关系数的计算操作 % % 输入: % X:输入的数值序列 % Y:输入的数值序列 % % 输出: % coeff:两个输入数值序列X,Y的相关系数 % if length(X) ~= length(Y) error('两个数值数列的维数不相等'); return; end fenzi = sum(X .* Y) - (sum(X) * sum(Y)) / length(X); fenmu = sqrt((sum(X .^2) - sum(X)^2 / length(X)) * (sum(Y .^2) - sum(Y)^2 / length(X))); coeff = fenzi / fenmu; end %函数myPearson结束
也可以使用Matlab中已有的函数计算皮尔逊相关系数:
而且不需要提前zscore(),因为自动会标准化(加了zscore和没加zscore结果是一样的)
coeff = corrcoef(X , Y);
或者直接使用:rst1=rst1+corr(rawdata(:,1),rawdata(:,i),'type','Pearson');
Spearman's rank correlation coefficient,也称为。在统计学中,斯皮尔曼等级相关系数以Charles Spearman命名,并经常用希腊字母ρ(rho)表示其值。斯皮尔曼等级相关系数用来估计两个变量X、Y之间的相关性,其中变量间的相关性可以使用单调函数来描述。如果两个变量取值的两个集合中均不存在相同的两个元素,那么,当其中一个变量可以表示为另一个变量的很好的单调函数时(即两个变量的变化趋势相同),两个变量之间的ρ可以达到+1或-1。
设两个随机变量分别为X、Y(也可以看做两个集合),它们的元素个数均为N,两个随即变量取的第i(1<=i<=N)个值分别用Xi、Yi表示。对X、Y进行排序(同时为升序或降序),得到两个元素排行集合x、y,其中元素xi、yi分别为Xi在X中的排行以及Yi在Y中的排行。将集合x、y中的元素对应相减得到一个排行差分集合d,其中di=xi-yi,1<=i<=N。随机变量X、Y之间的斯皮尔曼等级相关系数可以由x、y或者d计算得到,其计算方式如下所示:
由排行差分集合d计算而得(公式一):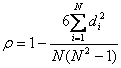
由排行集合x、y计算而得(斯皮尔曼等级相关系数同时也被认为是经过排行的两个随即变量的皮尔逊相关系数,以下实际是计算x、y的皮尔逊相关系数)(公式二):

以下是一个计算集合中元素排行的例子(仅适用于斯皮尔曼等级相关系数的计算)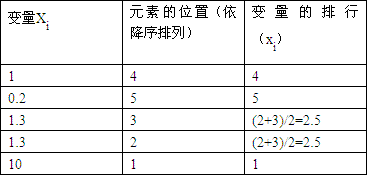
适用范围
斯皮尔曼等级相关系数对数据条件的要求没有皮尔逊相关系数严格,只要两个变量的观测值是成对的等级评定资料,或者是由连续变量观测资料转化得到的等级资料,不论两个变量的总体分布形态、样本容量的大小如何,都可以用斯皮尔曼等级相关系数来进行研究。
Matlab实现
依据排行差分集合d计算,使用上面的公式一
function coeff = mySpearman(X , Y) % 本函数用于实现斯皮尔曼等级相关系数的计算操作 % % 输入: % X:输入的数值序列 % Y:输入的数值序列 % % 输出: % coeff:两个输入数值序列X,Y的相关系数 if length(X) ~= length(Y) error('两个数值数列的维数不相等'); return; end N = length(X); %得到序列的长度 Xrank = zeros(1 , N); %存储X中各元素的排行 Yrank = zeros(1 , N); %存储Y中各元素的排行 %计算Xrank中的各个值 for i = 1 : N cont1 = 1; %记录大于特定元素的元素个数 cont2 = -1; %记录与特定元素相同的元素个数 for j = 1 : N if X(i) < X(j) cont1 = cont1 + 1; elseif X(i) == X(j) cont2 = cont2 + 1; end end Xrank(i) = cont1 + mean([0 : cont2]); end %计算Yrank中的各个值 for i = 1 : N cont1 = 1; %记录大于特定元素的元素个数 cont2 = -1; %记录与特定元素相同的元素个数 for j = 1 : N if Y(i) < Y(j) cont1 = cont1 + 1; elseif Y(i) == Y(j) cont2 = cont2 + 1; end end Yrank(i) = cont1 + mean([0 : cont2]); end %利用差分等级(或排行)序列计算斯皮尔曼等级相关系数 fenzi = 6 * sum((Xrank - Yrank).^2); fenmu = N * (N^2 - 1); coeff = 1 - fenzi / fenmu; end %函数mySpearman结束
源程序二:
使用Matlab中已有的函数计算斯皮尔曼等级相关系数(使用上面的公式二)
coeff = corr(X , Y , 'type' , 'Spearman');

参考链接(http://www.ilovematlab.cn/thread-47107-1-1.html)
price = [135,142,156,165,170,220,225,275,300,450];%原始数据 w=[95.3329,126.2888,152.0854,177.8820,203.6786,229.4753,255.2719,281.0685,332.6617,384.2549];%1阶拟合数据 std(abs(w-price)) RMSe=sqrt(sum((w-price).^2)/10)
MAE(平均绝对误差)

参考链接