20201007校测

T1

description:

现在给出一段 DNA 序列(字符集为4)，请帮他求出这段 DNA 序列中所有连续k个碱基形成的碱基序列中，出现最多的一种的出现次数。

data range:

(kle 10)
(Nle 5*10^6)

solution:

直接哈希模拟就可以了
不过观察到数据范围较大，用map会超时
于是可以用哈希表来实现
p.s.据说还有Trie树的神仙做法，但是不会啊

code:

#include<bits/stdc++.h>
using namespace std;
const int N=5e6+5,base=7,mod=91103991;
const int Z=1e6+7;
char ch[N];
int k,len,tot,hsh[N],pw[N];
vector<int>e[Z],num[Z];
inline int add(int x,int y){return x+y>=mod?x+y-mod:x+y;}
inline int dec(int x,int y){return x-y<0?x-y+mod:x-y;}
inline int cg(char c)
{
	if(c=='A')return 1;
	else if(c=='C')return 2;
	else if(c=='G')return 3;
	else return 4;
}
inline void pre()
{
	len=strlen(ch+1);
	hsh[0]=0,pw[0]=1;
	for(int i=1;i<=len;++i)
		hsh[i]=add(1ll*hsh[i-1]*base%mod,cg(ch[i])),pw[i]=1ll*base*pw[i-1]%mod;
}
inline int gethsh(int l,int r){return dec(hsh[r],1ll*hsh[l-1]*pw[r-l+1]%mod);}
int main()
{
	scanf("%s%d",ch+1,&k);
	pre();
	int ans=0;
	for(int i=k;i<=len;++i)
	{
		int hs=gethsh(i-k+1,i),ky=hs%Z;bool flag=0;
		for(int j=0;j<e[ky].size()&&!flag;++j)
			if(e[ky][j]==hs)flag=1,ans=max(ans,++num[ky][j]);
		if(!flag)e[ky].push_back(hs),num[ky].push_back(1),ans=max(ans,1);
	}
	cout<<ans;
	return 0;
}

T2

description:

有若干个二阶递推数列：(a_i=k*a_{i-1}+a_{i-2})对于每个数列都给定(k,a_0,a_1)
初始时给定集合s，对于每次询问输出使得(a_{s_i})最大的(s_i)和使得(a_{s_i`})最小的(s_i`),如果有多解输出最小的(s_i)

data range:

询问次数：(Nle 3*10^5)
集合s大小:(Mle 10^5)
集合元素(s_i)：(s_i<=10^9)
(0le k le 5000)

solution:

初看此题时毫无头绪
但是手玩几组样例后可以惊奇地发现
这个数列到最后一定是单调递增或者单调递减（容易发现就是(a_i)和(a_{i-1})同号时开始）
类似于这样:(单降同理)

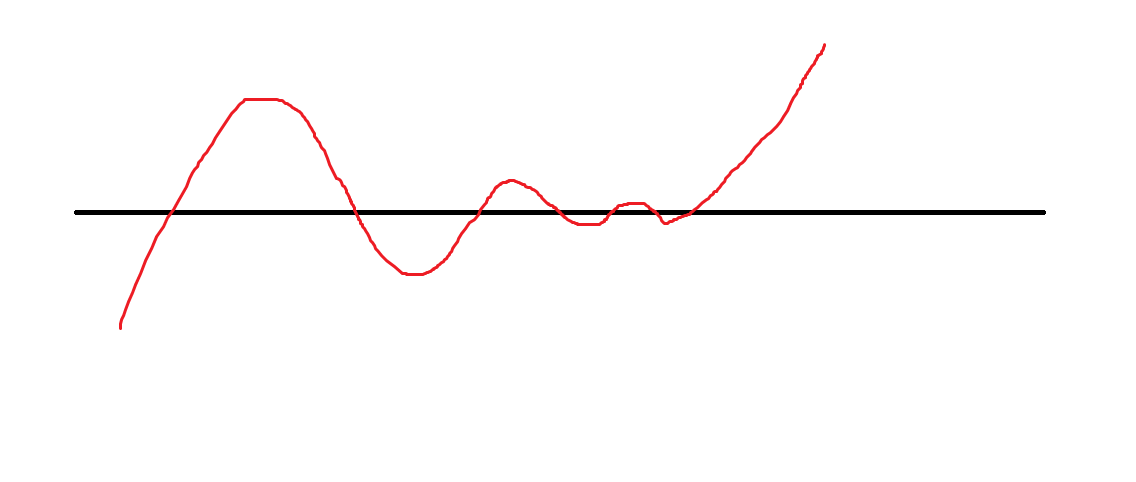
于是我们就可以一直枚举知道发现数列已经进入单增或单降阶段（可以证明这样做不超过(O(log_2n))然而并不会证）
但是有些细节还需注意:
进入单增或单降阶段后要判断(s_m)能否到达此处

code:

#include<bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+5;
int m,s[N],k;
ll a[N];
inline int read()
{
	int s=0,w=1; char ch=getchar();
	for(;!isdigit(ch);ch=getchar())if(ch=='-')w=-1;
	for(;isdigit(ch);ch=getchar())s=(s<<1)+(s<<3)+(ch^48);
	return s*w;
}
int main()
{
	m=read();
	for(int i=1;i<=m;++i)s[i]=read();
	int n=read();
	while(n--)
	{
		a[0]=1ll*read(),a[1]=1ll*read(),k=read();
		int lim=50;
		int mxp=s[1],mnp=s[1];
		ll mx=max(a[0],a[1]),mn=min(a[0],a[1]); 
		for(int i=2;i<=lim;++i)
		{
			a[i]=1ll*k*a[i-1]+a[i-2];
			if(a[i]>mx&&a[i-1]>=0&&a[i-2]>=0)lim=i;
                        //需要比当前最大值还要大，否则无法确定s[m]能否大过之前的数
			if(a[i]<mn&&a[i-1]<=0&&a[i-2]<=0)lim=i;
			mx=max(mx,a[i]),mn=min(mn,a[i]);
		}
		mx=-1e16,mn=1e16;
		for(int i=1;i<=m&&s[i]<lim;++i)
		{
			if(a[s[i]]>mx)mx=a[s[i]],mxp=s[i];
			if(a[s[i]]<mn)mn=a[s[i]],mnp=s[i];
		}
		if(s[m]>=lim&&a[lim]>0)mxp=s[m];
		if(s[m]>=lim&&a[lim]<0)mnp=s[m];
		printf("%d %d
",mxp,mnp);
	}
	return 0;
}

T3

description:

要求维护一个数据结构：

• 初始时有一些元素
• 插入一个元素（这个元素先前既没有被删除也没有被插入）
• 删除一个元素
• 插入一个最早被删除的元素

solution:

直接模拟然后用单调队列优化一波

code:

#include<bits/stdc++.h>
using namespace std;
const int N=2000005;
namespace IO
{
	int c;unsigned int seed;
	unsigned int randnum()
	{
		seed^=seed<<13;
		seed^=seed>>17;
		seed^=seed<<5;
		return seed;
	}
	inline int read(int &x){scanf("%d",&x);return x;}
	inline void init_case(int &m,int &a,int &b,int &d,int p[])
	{
		scanf("%d%u%d%d%d%d",&m,&seed,&a,&b,&c,&d);
		for(int i=1;i<=m;i++)
		{
			if(randnum()%c==0)p[i]=-1;
			else p[i]=randnum()%b;
		}
	}
	inline void update_ans(unsigned int &ans_sum,unsigned int cur_ans,int no)
	{
		const static unsigned int mod=998244353;
		ans_sum^=(long long)no*(no+7)%mod*cur_ans%mod;
	}
}
using IO::read;
using IO::init_case;
using IO::update_ans;
int p[N];
bool flag1[N],est[N];
deque<unsigned int>dq;
int q[N],h,t;
int pre[N],nxt[N],hd,tl;
inline void link(int l,int r){nxt[l]=r,pre[r]=l;}
int main()
{
	int T;read(T);
	int m,a,b,d;
	while(T--)
	{
		unsigned int ans_sum=0,cur_ans=0;
		init_case(m,a,b,d,p);int mx=max(a+1,b);
		fill(flag1,flag1+mx,0),fill(est,est+mx,0);
		dq.clear();hd=mx+1,tl=mx+2;
		for(int i=0;i<=a;++i)est[i]=true;
		for(int i=a+1;i<b;++i)link(i,i+1);
		if(a+1<=b)link(hd,a+1),link(b,tl);
		else link(hd,mx),link(mx,tl);
		h=1,t=0;
		for(int i=1;i<=m;i++)
		{
			if(p[i]==-1)
			{
				if(d)continue;
				if(dq.empty())cur_ans=0;
				else
				{
					unsigned int u=dq.front();
					if(h<=t&&q[h]==u)++h;
					est[u]=1;
					dq.pop_front();
					cur_ans=(h<=t?min(q[h],nxt[hd]):nxt[hd]);
				}
			}
			else if(p[i]>a&&!flag1[p[i]])
			{
				flag1[p[i]]=1,est[p[i]]=1;
				link(pre[p[i]],nxt[p[i]]);
				cur_ans=(h<=t?min(q[h],nxt[hd]):nxt[hd]);
			}
			else if(est[p[i]])
			{
				if(d)continue;
				est[p[i]]=0;
				while(h<=t&&q[t]>p[i])--t;
				q[++t]=p[i];
				dq.push_back(p[i]);
				cur_ans=(h<=t?min(q[h],nxt[hd]):nxt[hd]);
			}
			else
			{
				if(d)continue;
				if(dq.empty())cur_ans=0;
				else
				{
					unsigned int u=dq.front();
					if(h<=t&&q[h]==u)++h;
					est[u]=1;
					dq.pop_front();
					cur_ans=(h<=t?min(q[h],nxt[hd]):nxt[hd]);
				}
			}
			update_ans(ans_sum,cur_ans,i);
		}
		printf("%u
",ans_sum);
	}
	return 0;
}