计算几何基础

计算几何基础

UVA11178 Morley's Theorem
此题直接模拟即可，主要是熟悉向量基本运算

#include<bits/stdc++.h>
using namespace std;
typedef double db;
struct vec
{
	db x,y;
	inline void read(){scanf("%lf%lf",&x,&y);}
	inline void print(){printf("%.6lf %.6lf ",x,y);}
};
inline vec operator+(const vec&x,const vec&y){return {x.x+y.x,x.y+y.y};}//向量相加
inline vec operator-(const vec&x,const vec&y){return {x.x-y.x,x.y-y.y};}//向量相减
inline vec operator*(const db&x,const vec&y){return {x*y.x,x*y.y};}//向量数乘
inline db dot(const vec&x,const vec&y){return x.x*y.x+x.y*y.y;}//向量点乘
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}//向量叉乘
inline db len(const vec&x){return sqrt(x.x*x.x+x.y*x.y);}//向量模长
inline db ang(const vec&x,const vec&y){return acos(dot(x,y)/len(x)/len(y));}//向量夹角：dot(a,b)=|a||b|cos<a,b>
inline vec inr(const vec&P,const vec&v,const vec&Q,const vec&w)
{
	vec u=P-Q;
	double t1=cross(w,u)/cross(v,w);
	return P+t1*v;
}////直线焦点
inline vec rot(const vec&x,db rad)
{
	return {x.x*cos(rad)-x.y*sin(rad),x.x*sin(rad)+x.y*cos(rad)};
}//向量逆时针旋转rad
inline vec solve(const vec&A,const vec&B,const vec&C)
{
	vec v1=C-B;
	double a=ang(A-B,v1);
	v1=rot(v1,a/3);
	vec v2=B-C;
	double b=ang(A-C,v2);
	v2=rot(v2,-b/3);
	return inr(B,v1,C,v2);
}
vec A,B,C,D,E,F;
int main()
{
	int T;scanf("%d",&T);
	while(T--)
	{
		A.read(),B.read(),C.read();
		D=solve(A,B,C);
		E=solve(B,C,A);
		F=solve(C,A,B);
		D.print(),E.print(),F.print();puts("");
	}
	return 0;
}

UVA1342 That Nice Euler Circuit
求一个多边形把平面分成了多少个部分
此题主要是欧拉定理

[V+F-E=2 ]

因此求出顶点个数和边数即可
顶点个数可以线段两两求交后去重
边数可以每发现一个点在边上就把边数加一，原因是它会把当前边新分割出一部分

#include<bits/stdc++.h>
using namespace std;
typedef double db;
const int N=305;
const db eps=1e-7;
inline int sig(const db&x){return fabs(x)<eps?0:(x<0?-1:1);}
struct vec
{
	db x,y;
	inline void read(){scanf("%lf%lf",&x,&y);}
	inline void print(){printf("%.6lf %.6lf ",x,y);}
}p[N],v[N*N];
inline bool operator<(const vec&x,const vec&y){return x.x<y.x||(x.x==y.x&&x.y<y.y);}
inline bool operator==(const vec&x,const vec&y){return sig(x.x-y.x)==0&&sig(x.y-y.y)==0;}
inline vec operator+(const vec&x,const vec&y){return {x.x+y.x,x.y+y.y};}
inline vec operator-(const vec&x,const vec&y){return {x.x-y.x,x.y-y.y};}
inline vec operator*(const db&x,const vec&y){return {x*y.x,x*y.y};}
inline db dot(const vec&x,const vec&y){return x.x*y.x+x.y*y.y;}
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}
inline vec inr(const vec&P,const vec&v,const vec&Q,const vec&w)
{
	vec u=P-Q;
	double t1=cross(w,u)/cross(v,w);
	return P+t1*v;
}
inline bool pd(const vec&a1,const vec&a2,const vec&b1,const vec&b2)
{
	db c1,c2,c3,c4;
	c1=cross(a2-a1,b1-a1),c2=cross(a2-a1,b2-a1);
	c3=cross(b2-b1,a1-b1),c4=cross(b2-b1,a2-b1);
	return sig(c1)*sig(c2)<0&&sig(c3)*sig(c4)<0;
}//判断两线段是否规范相交：每一条线段的两个端点都在另一条线段的两侧
inline bool ons(const vec&p,const vec&a,const vec&b)
{
	return sig(cross(a-p,b-p))==0&&sig(dot(a-p,b-p))<0;
}//判断点是否在线段上：叉积为0且和线段两端连线的夹角是钝角（准确来说应该是平角）
int main()
{
	int kase=0,n;
	while(scanf("%d",&n)==1&&n)
	{
		for(int i=1;i<=n;++i)p[i].read(),v[i]=p[i];
		int c=n-1,e=n-1;
		for(int i=1;i<n;++i)
			for(int j=i+1;j<n;++j)
				if(pd(p[i],p[i+1],p[j],p[j+1]))
					v[++c]=inr(p[i],p[i+1]-p[i],p[j],p[j+1]-p[j]);
		sort(v+1,v+c+1);
		int tot=unique(v+1,v+c+1)-v-1;
		for(int i=1;i<=tot;++i)
			for(int j=1;j<n;++j)
				if(ons(v[i],p[j],p[j+1]))++e;
		printf("Case %d: There are %d pieces.
",++kase,e+2-tot);
	}
	return 0;
}

UVA12304 2D Geometry 110 in 1!
任务一：求三角形外接圆
中垂线求交点
任务二：求三角形内切圆
角平分线求交点
任务三：过已知点求已知圆的切线
可以通过点到圆心的距离判断解的个数

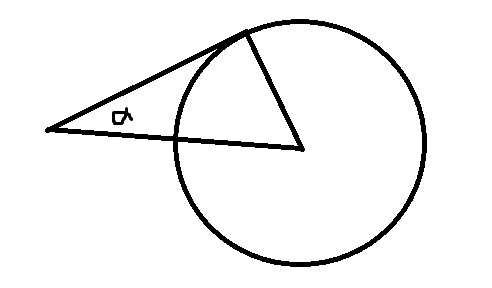
容易求出(alpha)，那么旋转一下就可以求出切线极角了
任务四：求所有点满足到定直线距离为(r)且到定点距离为(r)，其中(r)给定
将定直线延其垂直方向平移(r)可得两条直线
这两条直线和以定点为圆心，(r)为半径的圆求交点即可
任务五：求到两定直线距离为(r)的点，其中(r)给定
和任务四类似得到四条直线两两求交
任务六：求所有半径为(r)且和两给定圆外切的圆的圆心
将原先的两个圆的半径增加(r)，然后再求交点即可得到答案

#include<bits/stdc++.h>
using namespace std;
typedef double db;
const db eps=1e-8,pi=acos(-1.0);
inline int sig(const db&x){return fabs(x)<eps?0:(x<0?-1:1);}
struct vec
{
	db x,y;
	vec(db _x=0.0,db _y=0.0){x=_x,y=_y;}
	inline void read(){scanf("%lf%lf",&x,&y);}
	inline void print()const{printf("(%.6lf,%.6lf)",x,y);}
	inline bool operator==(const vec&rhs)const{return sig(x-rhs.x)==0&&sig(y-rhs.y)==0;}
	inline bool operator<(const vec&rhs)const{return sig(x-rhs.x)==0?sig(y-rhs.y)<0:sig(x-rhs.x)<0;}
	inline vec operator+(const vec&rhs)const{return vec(x+rhs.x,y+rhs.y);}
	inline vec operator-(const vec&rhs)const{return vec(x-rhs.x,y-rhs.y);}
	inline vec operator*(const db&p)const{return vec(p*x,p*y);}
	inline vec operator/(const db&p)const{return vec(x/p,y/p);}
	inline db len()const{return sqrt(x*x+y*y);}
	inline db ang()const{return atan2(y,x);}//向量极角
};
typedef vector<vec> vv;
inline db dot(const vec&x,const vec&y){return x.x*y.x+x.y*y.y;}
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}
inline vec rot(const vec&p,const db&rad){return vec(p.x*cos(rad)-p.y*sin(rad),p.x*sin(rad)+p.y*cos(rad));}
inline vec rot90(const vec&p){return vec(-p.y,p.x);}//求向量法向量
inline db ang(const vec&p,const vec&q){return acos(dot(p,q)/(p.len())/(q.len()));}
inline db todg(const db&x)
{
	db ans=x/pi*180;
	while(sig(ans)<0)ans+=180;
	while(sig(180-ans)<0)ans-=180;
	return ans;
}//弧度转度数
struct cir
{
	vec o;db r;
	inline void read(){o.read();scanf("%lf",&r);}
	inline db ang(const vec&p)const{return atan2(p.y-o.y,p.x-o.x);}
	inline vec pt(const db&rad)const{return vec(o.x+r*cos(rad),o.y+r*sin(rad));}//已知圆心角求点
};
inline db dis(const vec&P,const vec&Q){return (P-Q).len();}
inline db dis(const vec&P,const vec&v,const vec&Q)
{
	return fabs(cross(Q-P,v)/v.len());
}//点到直线距离
inline vec pro(const vec&P,const vec&v,const vec&Q)
{
	db t=dot(Q-P,v)/v.len();
	return P+v/v.len()*t;
}//点在直线上的投影
inline vec inr(const vec&P,const vec&v,const vec&Q,const vec&w)
{
	vec u=P-Q;
	db t=cross(u,w)/cross(w,v);
	return P+v*t;
}
inline int inr(const cir&c,const vec&P,const vec&v,vv&sol)
{
	db d=dis(P,v,c.o);
	if(sig(d-c.r)>0)return 0;
	else if(sig(d-c.r)==0)
	{
		sol.push_back(pro(P,v,c.o));
		return 1;
	}
	vec mid=pro(P,v,c.o),e=v/v.len();
	db l=sqrt(c.r*c.r-d*d);
	sol.push_back(mid+e*l);
	sol.push_back(mid-e*l);
	return 2;
}//圆和直线的交点：主要考虑垂径三角形
inline int inr(const cir&a,const cir&b,vv&sol)
{
	db d=dis(a.o,b.o);
	if(sig(d-a.r-b.r)>0)return 0;
	else if(sig(d-a.r-b.r)==0)
	{
		sol.push_back(a.pt(a.ang(b.o)));
		return 1;
	}
	db ag=a.ang(b.o),dl=acos((a.r*a.r+d*d-b.r*b.r)/(2*a.r*d));
	sol.push_back(a.pt(ag+dl));
	sol.push_back(a.pt(ag-dl));
	return 2;
}//圆和圆的交点
inline int gtg(const cir&a,const vec&P,vector<db>&sol)
{
	db d=dis(a.o,P);
	if(sig(a.r-d)>0)return 0;
	else if(sig(a.r-d==0))
	{
		sol.push_back(todg(rot90(P-a.o).ang()));
		return 1;
	}
	db dl=asin(a.r/d),ag=(a.o-P).ang();
	sol.push_back(todg(ag-dl));
	sol.push_back(todg(ag+dl));
	return 2;
}//求切线
inline void print(vv&ans)
{
	putchar('[');
	sort(ans.begin(),ans.end());int tot=ans.size();
	for(int i=0;i<tot;++i)ans[i].print(),printf(i==tot-1?"":",");
	putchar(']');puts("");
}
inline void print(vector<db>&ans)
{
	putchar('[');
	sort(ans.begin(),ans.end());int tot=ans.size();
	for(int i=0;i<tot;++i)printf("%.6lf",ans[i]),printf(i==tot-1?"":",");
	putchar(']');puts("");
}
char ch[200];
inline void solve1()
{
	vec A,B,C;A.read(),B.read(),C.read();
	vec ans=inr((A+B)/2,rot90(B-A),(B+C)/2,rot90(B-C));
	printf("(%.6lf,%.6lf,%.6lf)
",ans.x,ans.y,dis(ans,A));
}
inline void solve2()
{
	vec A,B,C;A.read(),B.read(),C.read();
	vec c=B-A,b=C-A,a=C-B;
	c=c/c.len(),a=a/a.len(),b=b/b.len();
	vec ans=inr(A,b+c,C,a+b);
	printf("(%.6lf,%.6lf,%.6lf)
",ans.x,ans.y,dis(A,B-A,ans));
}
inline void solve3()
{
	vector<db>sol;
	cir c;vec t;c.read(),t.read();
	gtg(c,t,sol);print(sol);
}
inline void solve4()
{
	vec P,A,B;db r;P.read(),A.read(),B.read();scanf("%lf",&r);
	vec e=rot90(B-A)/dis(B,A);
	vec C=A+e*r,D=A-e*r;vv sol;
	cir c;c.o=P,c.r=r;
	inr(c,C,B-A,sol);inr(c,D,B-A,sol);
	print(sol);
}
inline void solve5()
{
	vec A,B,C,D;db r;
	A.read(),B.read(),C.read(),D.read();scanf("%lf",&r);
	vec e1=rot90(B-A)/dis(B,A),e2=rot90(D-C)/dis(D,C);
	vec A1=A+e1*r,A2=A-e1*r,C1=C+e2*r,C2=C-e2*r;vv sol;
	sol.push_back(inr(A1,B-A,C1,D-C));
	sol.push_back(inr(A2,B-A,C1,D-C));
	sol.push_back(inr(A1,B-A,C2,D-C));
	sol.push_back(inr(A2,B-A,C2,D-C));print(sol);
}
inline void solve6()
{
	cir a,b;db r;a.read(),b.read();scanf("%lf",&r);
	a.r+=r,b.r+=r;vv sol;
	inr(a,b,sol);print(sol);
}
int main()
{
	while(scanf("%s",ch)!=EOF)
	{
		if(ch[0]=='I')solve2();
		else if(ch[0]=='T')solve3();
		else if(ch[4]=='u')solve1();
		else if(ch[7]=='h')solve4();
		else if(ch[18]=='L')solve5();
		else solve6();
	}
	return 0;
}

UVA10652 Board Wrapping
直接上凸包就可以了
考虑(Andrew)算法，将所有点按照(x)从小到大排序，若相同则按照(y)从小到大排序
从前往后扫，同时用栈记下当前在凸包中的点，如果新加入的点和之前的点形成凹进去的图形则弹栈（可以用叉积正负判断（右手定则））
这样可以求出下图壳
同理求出上图壳

#include<bits/stdc++.h>
using namespace std;
typedef double db;
const int N=2505;
const db eps=1e-7,pi=acos(-1.0);
inline int sig(const db&x){return fabs(x)<eps?0:(x<0?-1:1);}
struct vec{db x,y;}p[N],q[N];
inline bool operator<(const vec&x,const vec&y){return x.x<y.x||(x.x==y.x&&x.y<y.y);}
inline bool operator==(const vec&x,const vec&y){return sig(x.x-y.x)==0&&sig(x.y-y.y)==0;}
inline vec operator+(const vec&x,const vec&y){return {x.x+y.x,x.y+y.y};}
inline vec operator-(const vec&x,const vec&y){return {x.x-y.x,x.y-y.y};}
inline db cross(const vec&x,const vec&y){return x.x*y.y-x.y*y.x;}
inline db torad(const db&x){return x/180*pi;} 
inline vec rot(const vec&x,db rad)
{
	return {x.x*cos(rad)-x.y*sin(rad),x.x*sin(rad)+x.y*cos(rad)};
}
inline int Andrew(int n)
{
	sort(p+1,p+n+1);int m=0;
	for(int i=1;i<=n;++i)
	{
		while(m>1&&sig(cross(q[m]-q[m-1],p[i]-q[m-1]))<=0)--m;
		q[++m]=p[i];
	}
	int k=m;
	for(int i=n-1;i;--i)
	{
		while(m>k&&sig(cross(q[m]-q[m-1],p[i]-q[m-1]))<=0)--m;
		q[++m]=p[i];
	}
	m-=n>1;return m;
}
inline db S(int n)
{
	db ans=0.0;
	for(int i=2;i<n;++i)
		ans+=cross(q[i]-q[1],q[i+1]-q[1]);
	ans/=2;
	return fabs(ans);
}//三角剖分求多边形面积
int main()
{
	int T;scanf("%d",&T);
	while(T--)
	{
		int n,tot=0;scanf("%d",&n);
		db S1=0.0,S2=0.0;
		for(int i=1;i<=n;++i)
		{
			db x,y,w,h,j;
			scanf("%lf%lf%lf%lf%lf",&x,&y,&w,&h,&j);
			j=-torad(j);vec o={x,y};
			p[++tot]=o+rot({w/2,h/2},j);
			p[++tot]=o+rot({w/2,-h/2},j);
			p[++tot]=o+rot({-w/2,h/2},j);
			p[++tot]=o+rot({-w/2,-h/2},j);
			S1+=w*h;
		}
		S2=S(Andrew(tot));
		printf("%.1lf %%
",S1*100/S2);
	}
	return 0;
}