把以前考试换根题集中写一下
随便选一个点做根一遍$dfs$求子树内贡献,再通过特殊手段算$ans[1]$,最后$dfs$求其他$ans$
拆成子树内,子树外分别算贡献差,得儿子是很常见套路了
小奇的仓库

$M<=15$
题解
很久之前做的换根dp,当时觉得真是神仙,现在看还是觉得很神仙
不同于一般换根dp,这个题$n^2$并不好写
所以$n^2$算法就省略了
考虑$M$非常小,可以计算$M$对答案影响
一个直接的想法是先算出来原答案,再减去现在答案
//本来为j现在异或M,变化了j-delta //你都按j算的 //本来j,现在j-1 delta=1 //所有结果减1
考虑如何算出原答案,对于一个点来说很好算,我们要用一次换根算出来其他点答案
$ans[1]=sumlimits_{i=2}^{n}dis[i]$
换根
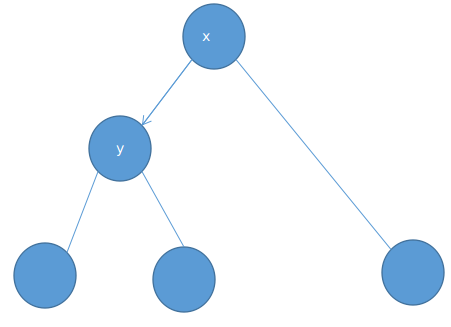
思考 从x转移到y,那么你子树内点贡献减少edg,子树外点贡献增加edg
那么$ans[y]=ans[x]-sz[y]*edg+(n-sz[y])*edg$
然后考虑算delta
$f[x][i]$表示x子树内路径长mod16后为i条数
转移$f[x][i+edg]=sumlimits_{y}^{yin son} f[y][i]$
$g[x][i]$表示整棵树内路径长mod16后为i条数
初始$g[1]=f[1]$
考虑换根
分为几部分贡献,子树内,子树外
子树内很简单$g[y][i]+=f[y][i]$
子树外$g[y][edg+j]+=g[x][j]$即子树外距离当前为$j$的加上当前$edg$即为到当前点$edg+j$的
但这样会算重,$g[x][j]$我们把它当作子树外的了,实际它是整棵树贡献,$g$要减去子树内贡献
$-f[y][j-edg]$即可,子树内要到x距离为$j$那么到$y$距离肯定为$j-edg$
代码

#include<bits/stdc++.h> using namespace std; #define ll long long #define A 1010101 #define mod 16 ll head[A],ver[A],nxt[A],edg[A],f[A][30],g[A][30],sum[A],dis[A],sz[A],ans[A]; ll tot=1,n,m,M; void add(ll x,ll y,ll z){ ver[++tot]=y,nxt[tot]=head[x],head[x]=tot,edg[tot]=z; } void dfs(ll x,ll pre){ sz[x]=1; for(ll i=head[x];i;i=nxt[i]){ ll y=ver[i]; if(y==pre) continue ; dis[y]=dis[x]+edg[i]; dfs(y,x); sz[x]+=sz[y]; } } void dfs0(ll x,ll pre){ for(ll i=head[x];i;i=nxt[i]){ ll y=ver[i]; if(y==pre) continue ; ans[y]=ans[x]-(sz[y]*edg[i])+((n-sz[y])*edg[i]); dfs0(y,x); } } void dfs1(ll x,ll pre){ f[x][0]=1; for(ll i=head[x];i;i=nxt[i]){ ll y=ver[i]; if(y==pre) continue ; dfs1(y,x); for(ll j=0;j<=15;j++) f[x][(j+edg[i])%mod]+=f[y][j]; } } void dfs2(ll x,ll pre){ for(ll i=head[x];i;i=nxt[i]){ ll y=ver[i]; if(y==pre) continue ; for(ll j=0;j<=15;j++) g[y][(j+edg[i])%mod]+=f[y][(j+edg[i])%mod]+(g[x][j]-f[y][(j-edg[i]%mod+mod)%mod]);// dfs2(y,x); } } int main(){ // freopen("da.in","r",stdin);freopen("ans.bf","w",stdout); scanf("%lld%lld",&n,&M); for(ll i=1,a,b,c;i<=n-1;i++){ scanf("%lld%lld%lld",&a,&b,&c); add(a,b,c);add(b,a,c); } dis[0]=0; dfs(1,0); for(ll i=2;i<=n;i++) ans[1]+=dis[i]; dfs0(1,0); dfs1(1,0); for(ll i=0;i<=15;i++) g[1][i]=f[1][i]; dfs2(1,0); for(ll i=1;i<=n;i++){ g[i][0]--; for(ll j=0;j<=15;j++){ ll delta; delta=(j-(j^M)); //本来为j现在异或M,变化了j-delta //你都按j算的 //本来j,现在j-1 delta=1 //所有结果减1 ans[i]-=delta*g[i][j]; // printf("g[%lld][%lld]=%lld ",i,j,g[i][j]); } printf("%lld ",ans[i]); } }
randomwalking

题解
$n^2$很简单,考虑换根
$f[x][0]$表示子树内走到当前期望
随便选一个做根
对于非根节点:$f[x][0]=a[x]+sumlimits_{y}^{yin son[x]} frac{1}{deg[x]-1} f[y][0]$
对于根:$f[x][0]=a[x]+sumlimits_{y}^{yin son[x]} frac{1}{deg[x]} f[y][0]$
$f[x][1]$表示整棵树走到当前期望
$f[1][1]=f[1][0]$
考虑换根

仍分为子树内子树外
子树内贡献就是$(f[y][0]-a[y])*(deg[y]-1)$
子树外看似很难求但还是可求的
看从$x$转移到$y$
$(f[x][1]-a[x])*deg$求出$y$子树和别的子树贡献
$(f[x][1]-a[x])*deg-f[y][0]$就是子树外的
还有一个注意点,本来$x$为根现在$y$为根了,$x$本来出度为$2$现在变为了$1$deg也要变化
$f[y][1]=frac{(frac{((f[x][1]-a[x])*deg[x]-f[y][0])}{(deg[x]-1)}+a[x]+(f[y][0]-a[y])*(deg[y]-1))}{deg[y]}+a[y];$
代码

#include<bits/stdc++.h> using namespace std; #define ll long long #define A 2222222 ll sz[A],a[A],head[A],nxt[A],ver[A]; ll n,tot,id; double deg[A],f[A][2]; void add(ll x,ll y){ nxt[++tot]=head[x],head[x]=tot,ver[tot]=y; } void dpfs(ll x,ll pre){ for(ll i=head[x];i;i=nxt[i]){ ll y=ver[i]; if(y==pre) continue ; dpfs(y,x); if(pre==0) f[x][0]+=f[y][0]*1/(deg[x]); else f[x][0]+=f[y][0]*1/(deg[x]-1); } f[x][0]+=a[x]; // printf("f[%lld]=%.3lf ",x,f[x][0]); } void dpfs2(ll x,ll pre){ for(ll i=head[x];i;i=nxt[i]){ ll y=ver[i]; if(y==pre) continue ; double tmp1=(f[x][1]-a[x])*deg[x]; double tmp2=tmp1-f[y][0]; double tmp3=(f[y][0]-a[y])*(deg[y]-1); if(deg[x]>1) f[y][1]=(tmp2/(deg[x]-1)+a[x]+tmp3)/deg[y]+a[y]; else f[y][1]=(a[x]+tmp3)/deg[y]+a[y]; // printf("x=%lld tmp1=%.3lf f[%lld]=%.3lf deg=%.3lf tmp2=%.3lf tmp3=%.3lf f[%lld][1]=%.3lf ",x,tmp1,x,f[x][1]-a[x],deg[x],tmp2,tmp3,y,f[y][1]); } for(ll i=head[x];i;i=nxt[i]){ ll y=ver[i]; if(y==pre) continue ; dpfs2(y,x); } } void sub_task1(){ dpfs(1,0);f[1][1]=f[1][0]; dpfs2(1,0); id=1; for(ll i=1;i<=n;i++) if(f[i][1]<f[id][1]) id=i; printf("%lld ",id); } int main(){ scanf("%lld",&n); for(ll i=1;i<=n;i++){ scanf("%lld",&a[i]); } for(ll i=1,c,b;i<n;i++){ scanf("%lld%lld",&b,&c); add(b,c);add(c,b); deg[b]++,deg[c]++; } sub_task1(); }
