梯度检验的意义：为了验证求导代码是否正确
思路：利用导数的定义
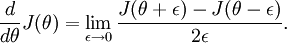
可以去任意theta值对等式左边的导数用：
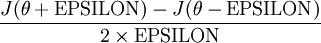
来近似。一般EPSILON用一个很小的常量（10-4数量级，不宜太小）
因此若存在计算deltaJ（θ）的函数g（θ），则：
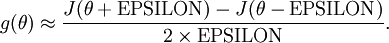
来检验函数是否正确，一般正常情况左右两端至少有四位有效数字是一样的（EPSILON = 10-4下）
对于实际操作下的向量情况，进行合理的改造即可：
对于计算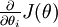
的函数
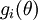，我们想要检验其结果，可以定义
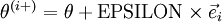，其中
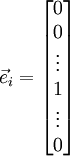
是第i个基向量，维度同θ，只在第i行有个1其他都是0。
同理可以定义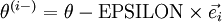
，这样检验式变成了：
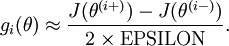
该方法主要运用于原算法中计算J（W，b）的导数环节