Pruning Filters For Efficient ConvNets
1. Introduction
CNN在不同应用中取得的成功伴随着参数存储成本和计算量的增加,最近朝着减少这些花销的努力涉及到剪枝和压缩不同层的权重,并且是在不损伤精度的条件下。然而,基于幅值的权重剪枝主要是减少了全连接层的参数量,并且由于修剪的不规则性,并没有减少卷积层的计算成本。我们展示了一种对于CNN的加速方法,我们直接移除对于CNN精度影响很小的卷积核。通过将网络的这些卷积核以及它们的feature map移除掉,可以极大的减少计算成本。与权重剪枝相比,这个方法不会导致稀疏连接模式,因此,它也不需要专门支持稀疏卷积库的支持,它可以使用针对密集矩阵乘法的BLAS库高效处理,我们展示了通过简单的卷积核剪枝可以推理成本,在CIFAR10上,VGG-16的推理成本可降低高达34%,ResNet-110最高可降低38%,同时通过重新训练网络恢复接近原始精度。
(以往的剪枝大多数是对全连接层直接下手,本文是从卷积层角度来切入,通过对精度影响很小的卷积核进行剪枝,同时将网络中与之相对应的feature map进行移除,就能减少计算成本。)
2. Pruning Filters and Feature Maps
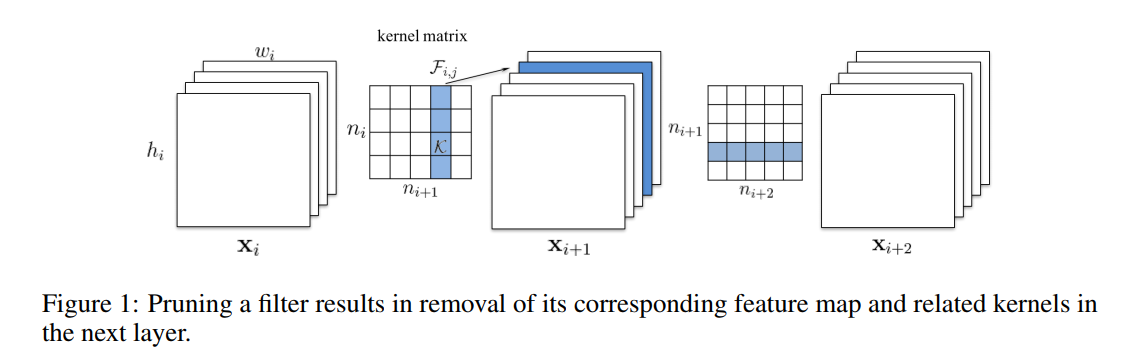
$n_{i}$ 是第i个卷积层的输入通道数,$h_{i} / w_{i}$是输入特征图的宽和高。卷积层将输入维度为 $X_{i} subset R^{n_{i} imes h_{i} imes w_{i}}$的特征图转化为维度为 $X_{i+1} subset R^{n_{i+1} imes h_{i+1} imes w_{i+1}}$的输出特征图,可以直接当作下一个卷积层的输入。这里卷积核的维度为 $n_{i+1} imes n_{i} imes k imes k$,卷积层的MAdd次数为 $n_{i+1} imes n_{i} imes k^{2} imes h_{i+1} imes w_{i+1}$ 。当如Figure 1所示的那样,将一个卷积核剪掉,对应的一个feature map就没了,减少了 $n_{i} imes k^{2} imes h_{i+1} imes w_{i+1}$次运算,同时由此输出通道数的减少导致下一层的卷积通道维度的缩减,又减少了 $n_{i+2} imes k^{2} imes h_{i+2} imes w_{i+2}$ 。原因在于:当前一个卷积层的卷积核被剪掉以后,该层保留的卷积核参数不仅是在卷积核个数这个维度上缩减了,还和上一个卷积层剪掉的卷积核个数有关,因此其间接导致了该层卷积核在通道维度的缩减。
3. Pruning
3.1 Determining which filters to prune within a single layer
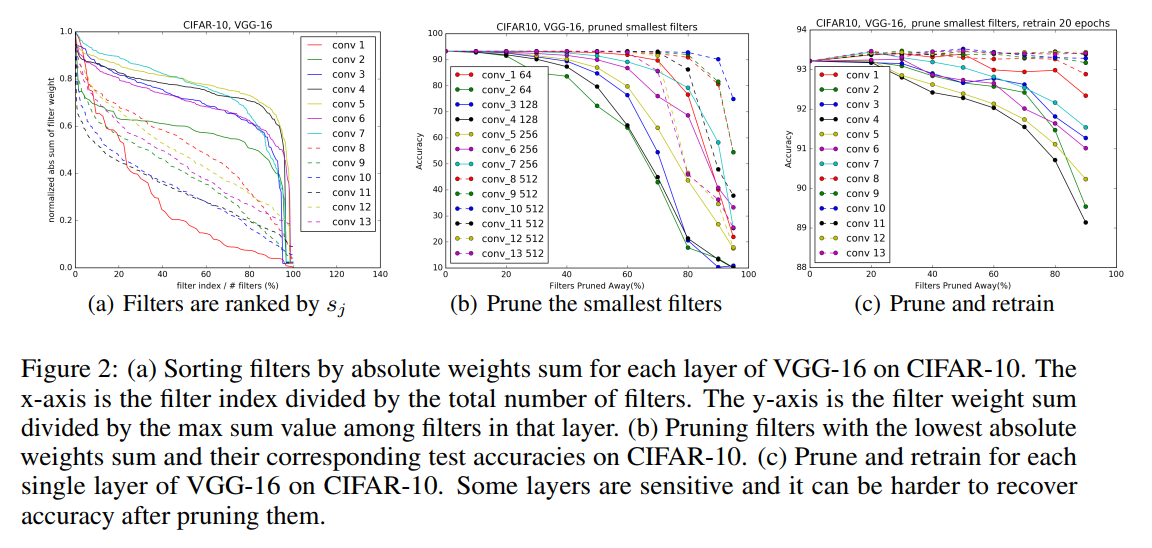
$F_{i, j} subset R^{n_{i} imes k imes k}$表示第i层的一个卷积核,我们通过 $sumleft|mathcal{F}_{i, j} ight|$(一个卷积核内所有权值绝对值的和——L1正则项)来表征每个层中该卷积核的重要性。Figure 2(a)展示了在CIFAR-10数据集上训练好的VGG-16网络中每一个卷积层中每个卷积核权重绝对值之和的分布,可以看到每层的分布是不同的,我们发现剪掉值最小的卷积核比随机(或剪最大)的效果要好,相比于基于其他的标准来衡量卷积核的重要性(比如基于激活值的feature map剪枝),l1-norm确实是一个很好的选择卷积核的方法。
从第i个卷积层剪掉m个卷积核的过程如下:
1. 对每个卷积核$F_{i, j}$,计算它的权重绝对值之和$s_{j}=sum_{l=1}^{n_{i}} sum_{l}left|K_{l} ight|$;
2. 根据 $s_{j}$排序;
3. 将m个权重绝对值之和最小的卷积核以及对应的feature maps剪掉。下一个卷积层中与剪掉的feature maps相关的核也要移除;
4. 一个对于第i层和第i+1层的新的权重矩阵被创建,并且剩下的权重参数被复制到新模型中;
3.2 Determining single layer's sensitivity to pruning
为了弄清楚每层的敏感度,我们对每一层独立剪枝并在验证集上对剪枝后的网络进行评估。Figure 2(b)展示了结果,很明显斜率比较平缓的层对剪枝的敏感度更高,我们根据经验来决定对每一层的卷积核进行剪枝,对于深度网络(如VGG-16或ResNets),我们观察到同一stage(相同尺寸的特征图)对应的层对剪枝的敏感度相似,为了避免引入layer-wise meta-parameters,我们对于同一stage的所有层使用相同的剪枝比例。对于那些敏感度高的层,我们剪枝时比例很小,甚至完全不进行剪枝。
3.3 Puring filters across multiple layers
之前的工作是逐层剪枝,然后重复训练来恢复精度。然而,理解如何能一次性对多层进行剪枝是非常有必要的:
1. 对于深度网络,逐层剪枝再训练太耗时;
2. 整体剪枝的方法提供给网络稳健性的一个全面视野,从而导致产生一个更小的网络;
3. 对于复杂的网络,一个整体的方法很有必要,比如对于ResNet,对恒等映射特征图或者每个残差模块的第二个层剪枝会导致额外层的修剪;
为了对多层同时剪枝,我们考虑了两个策略:
1. 每一层独立剪枝,即在计算(求权重绝对值之和)时不考虑上一层的修剪情况,所以计算时下图中的黄点仍然参与计算;
2. 贪心策略,计算时不计算已经修剪过的,即黄点不参与计算;
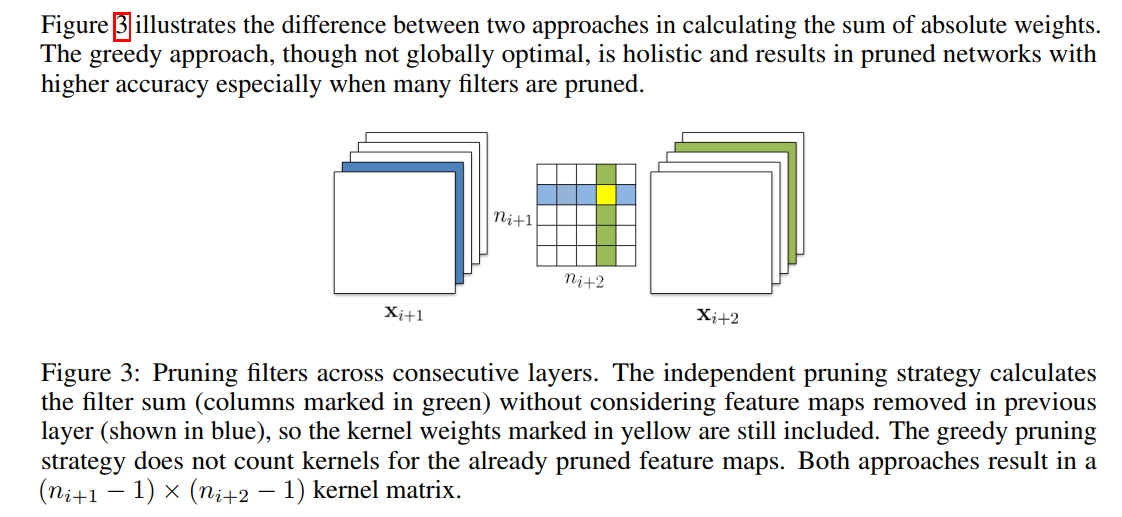
上图说明了两种方法之间的区别,实验结果证明第二种方法精度会高一点。
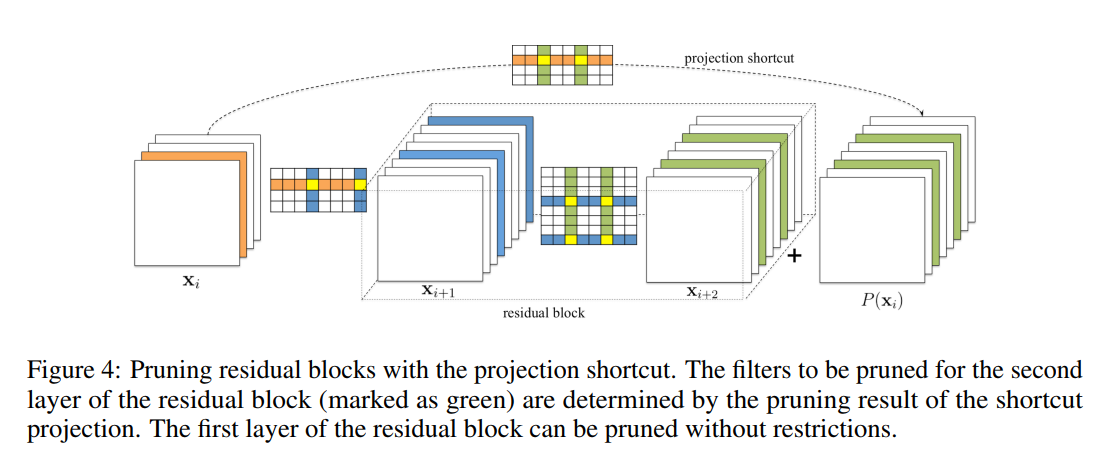
对于简单的CNN网络,如VGGNet和AlexNet,我们可以简单的对任意卷积层剪枝。然而,对于如ResNet这样的复杂网络,这是不可行的。ResNet的结构对剪枝提出了限制条件,残差块中的第一个卷积层可以随意修剪,因为它不会改变残差块输出特征图的数目,然而第二个卷积层和特征映射的剪枝很困难。因此,为了残差模块的第二个卷积层进行剪枝,相关的projected featured maps必须也要剪掉,由于恒等特征映射要比添加的residual maps重要,对第二个层的剪枝应该由shortcut层的剪枝结果决定。为了决定那些恒等特征映射图被剪掉,我们对shortcut卷积层(1x1卷积核)上采用相同的选择标准,即residual block 中第二层修剪的 Filter index 与shortcut layer 所选择的 Filter index 相同。
3.4 Retrained pruned networks to regain accuracy
在剪枝过后,通过预训练可以补偿剪枝造成的精度损失,有两种策略:
1. 一次剪枝和重新训练:一次性对多层的卷积核剪枝,然后重新训练直到原来的准确率恢复;
2. 交替剪枝和训练:逐层或逐卷积核剪枝,然后再训练,重复多次。
对于具有修剪弹性的层,第一种方法可以用于删除网络的重要部分,并且可以通过短时间重新训练来恢复精度(小于原始训练时间)。但是,当敏感层的一些 Filter 被剪掉或大部分网络被剪掉时,可能无法恢复原始精度。这时第二种方法可能会产生更好的结果,但迭代过程需要更多的 epochs,特别是对于非常深的网络。
4. 实验结果
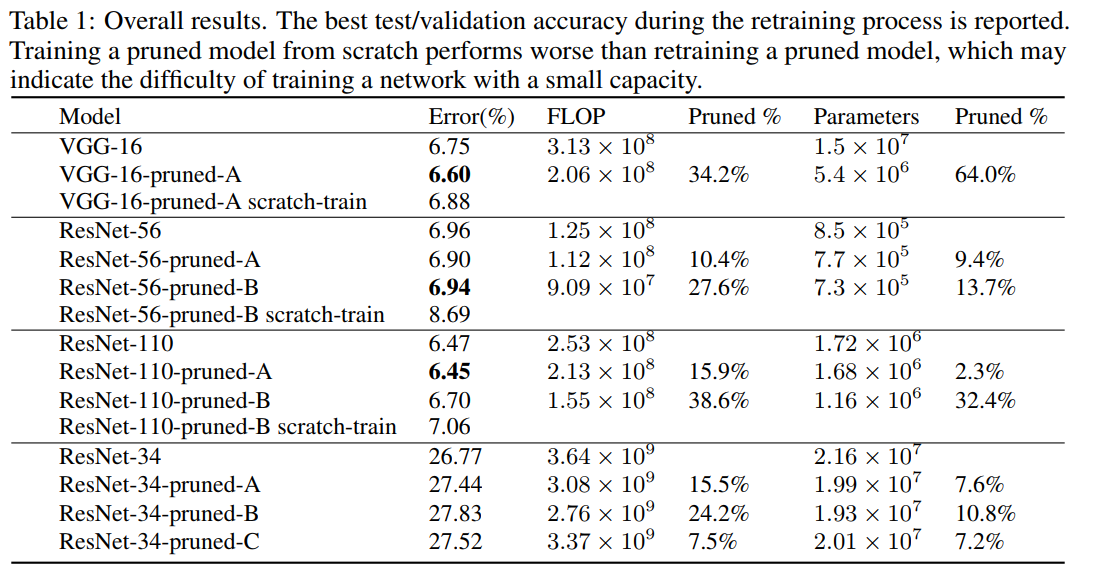
从table 1可以看出来,对剪枝后的网络结构从头训练要比对重新训练剪枝后的网络(利用了未剪枝之前的权重)的结果差,这也说明了对小容量的网络训练很难。
VGG-16中各层的剪枝比例如下:
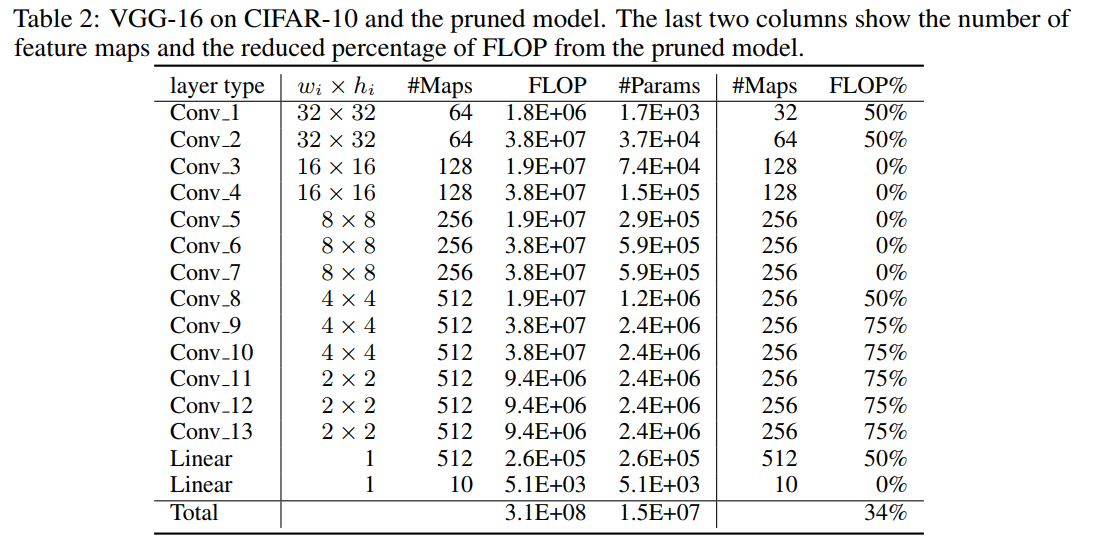
参考资料: https://mp.weixin.qq.com/s?__biz=MzA4MjY4NTk0NQ==&mid=2247484370&idx=1&sn=a9629408dc3518144c7aa4fe72be9299&chksm=9f80b944a8f730520d6d000272b716c4b394ec5722909d365ce8d88acd09209a4282baaf2939&scene=21#wechat_redirect
https://zhuanlan.zhihu.com/p/63779916