Numpy基础总结

一、文件读取

　　numpy.genfromtxt() 可以用来读取各种文件。常用语法大致如下：

　　numpy.genfromtxt(fname, dtype=<type 'float'>, delimiter=None, skip_header=0, skip_footer=0)

　　fname 要导入的文件路径

　　dtype 指定要导入文件的类型，dtype=str / int等等

　　delimiter  文件中不同元素间的间隔方式，空格还是逗号什么的，如：delimiter=','；

　　skip_header 是否跳过开头行，一般第一行为类别，为0不跳过，为1或者2则跳过前面1或者2行

　　

import numpy

students = numpy.genfromtxt("student_list.txt", delimiter=",",dtype=str, skip_header=0)

二、构造ndarray

　　1、NumPy的数组类被称作ndarray，通常被称作数组。

　　np.array只是一个便捷的函数，用来创建一个ndarray，它本身不是一个类。

　　ndarray：N维数组对象（矩阵），所有元素必须是相同类型。 
　　ndarray属性：

　　　　ndim属性，表示维度个数；

　　　　shape属性，表示各维度大小；

　　　　dtype属性，表示数据类型。

　  创建ndarray数组函数：

　　

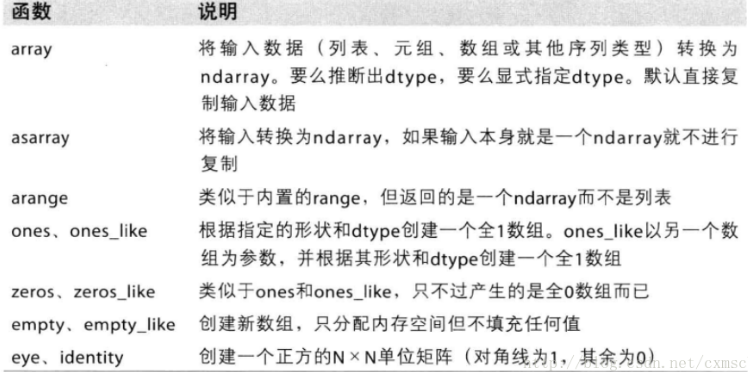
　　array和asarray都可以将结构数据转化为ndarray，但是主要区别就是当数据源是ndarray时，array仍然会copy出一个副本，占用新的内存，但asarray不会，直接指向A的地址。

　　numpy.array()构造 ndarray

　　numpy.array()中传入数组参数，可以是一维的也可以是二维三维的。numpy 会将其转变成 ndarray 的结构。

vector = numpy.array([1,2,3,4])
matrix = numpy.array([[1,2,3],[4,5,6]])

　　传入的参数必须是同一结构,不是同一结构将发生转换。

vector = numpy.array([1,2,3,4])       # 均为int型

array([1, 2, 3, 4])

vector = numpy.array([1,2,3,4.0])  # 转为float类型

array([ 1.,  2.,  3.,  4.])

vector = numpy.array([1,2,'3',4])   # 转为str类型

array(['1', '2', '3', '4'],dtype='<U21')

　　利用 .shape 查看结构

　　能够了解 array 的结构，debug 时通过查看结构能够更好地了解程序运行的过程。

print(vector.shape)
print(matrix.shape)
(4,)
(2, 3)

　　利用 dtype 查看类型

vector = numpy.array([1,2,3,4])
vector.dtype

dtype('int64')

　　ndim 查看维度

vector = numpy.array([1,2,3,4])
vector.ndim

1

matrix = numpy.array([[1,2,3],
                      [4,5,6],
                     [7,8,9]])
matrix.ndim

2

　　size 查看元素数量

matrix.size
9

　　2、数组和矩阵matrix的区别（matrix 和 array的区别）

• Numpy matrix必须是2维的,但是 numpy arrays (ndarrays) 可以是多维的（1D，2D，3D····ND）. Matrix是Array的一个小的分支，包含于Array。所以matrix 拥有array的所有特性。但这时候，官方建议大家如果两个可以通用，那就选择array，因为array更灵活，速度更快，很多人把二维的array也翻译成矩阵。
• 但是matrix的优势就是相对简单的运算符号，比如两个矩阵相乘，就是用符号*，但是array相乘不能这么用，得用方法.dot()
• matrix 和 array 都可以通过objects后面加.T 得到其转置。但是 matrix objects 还可以在后面加 .H 得到共轭矩阵, 加 .I 得到逆矩阵。
• 在numpy里面arrays遵从逐个元素的运算，所以array：c 和d的c*d为对应元素相乘，而矩阵相乘，则需要numpy里面的dot命令 。

a=np.mat('4 3; 2 1')
b=np.mat('1 2; 3 4')
print(a)
# [[4 3]
#  [2 1]]
print(b)
# [[1 2]
#  [3 4]]
print(a*b)
# [[13 20]
#  [ 5  8]]
c=np.array([[4, 3], [2, 1]])
d=np.array([[1, 2], [3, 4]])
print(c*d)
# [[4 6]
#  [6 4]]
print(np.dot(c,d)) 
# [[13 20] # [ 5 8]]

>>> a=np.mat([[4+2j 3], [2 1]])
>>> a
matrix([[ 4.+2.j,  3.+0.j],
        [ 2.+0.j,  1.+0.j]])
>>> a.H
matrix([[ 4.-2.j,  2.-0.j],
        [ 3.-0.j,  1.-0.j]])
>>> a.I
matrix([[-0.25-0.25j,  0.75+0.75j],
        [ 0.50+0.5j , -0.50-1.5j ]])>>> b=np.array([[4, 3], [2, 1]])
>>> b.T
array([[4, 2],
       [3, 1]])
>>> b.H
Traceback (most recent call last):
  File "<stdin>", line 1, in <module>
AttributeError: 'numpy.ndarray' object has no attribute 'H'

• ** 运算符的作用也不一样 　

a=np.mat([[4,3], [2,1]])
c=np.array([[4, 3], [2, 1]])
print(a**2)
# [[22 15]
#  [10  7]]
print(c**2)
# [[16  9]
#  [ 4  1]]

　　因为a是个matrix，所以a**2返回的是a*a，相当于矩阵相乘。而c是array，c**2相当于，c中的元素逐个求平方。

　　问题就出来了，如果一个程序里面既有matrix 又有array，会让人脑袋大。但是如果只用array，你不仅可以实现matrix所有的功能，还减少了编程和阅读的麻烦。

三、获取与计算

　　numpy 能使用切片获取数据

matrix = numpy.array([[1,2,3],
                      [4,5,6],
                     [7,8,9]])
>>> matrix[1,1]
5
>>> matrix[0,2]
3
>>> matrix[1,]
array([4, 5, 6])
>>> matrix[1]
array([4, 5, 6])
>>> matrix[1][0]
4
>>> matrix[:,1]
array([2, 5, 8])

　>>> matrix[1,...]
  array([4, 5, 6])
  >>> matrix[...,1]
  array([2, 5, 8])

　　根据条件获取

　　numpy 能够依次比较 vector 和元素之间是否相同

vector = numpy.array([5, 10, 15, 20])
vector == 10

array([False,  True, False, False], dtype=bool)

vector = numpy.array([5, 10, 15, 20])
equal_to_ten = (vector == 10)
print(equal_to_ten)
print(vector[equal_to_ten])

[False  True False False]
[10]

vector = numpy.array([5, 10, 15, 20])
equal_to_ten_and_five = (vector == 10) & (vector == 5)

vector = numpy.array([5, 10, 15, 20])
equal_to_ten_or_five = (vector == 10) | (vector == 5)

　　类型转换

　　将整体类型进行转换

vector = numpy.array([5, 10, 15, 20])
print(vector.dtype)
vector = vector.astype(str)
print(vector.dtype)

int64
<U21

　　求和

　　sum() 能够对 ndarray 进行各种求和操作，比如分别按行按列进行求和，sum(1) 是 sum(axis=1)) 的缩写，1表示按照 x轴方向求和，0表示按照y轴方向求和

matrix = numpy.array([[1,2,3],
                      [4,5,6],
                     [7,8,9]])
print(matrix.sum())
print(matrix.sum(1))
print(matrix.sum(0))

45
[ 6 15 24]
[12 15 18]

 

四、 常用函数

　　reshape

　　生成从 0-14 的 15 个数字，使用 reshape(3,5) 将其构造成一个三行五列的 array。

 　　resize和reshape都可以改变ndarray的结构，但resize会对原值进行修改，返回None，而reshape不会对原值进行修改，返回是修改后结果。

import numpy as np
arr = np.arange(15).reshape(3, 5)
arr

array([[ 0,  1,  2,  3,  4],
       [ 5,  6,  7,  8,  9],
       [10, 11, 12, 13, 14]])

　zeros

　　生成指定结构的默认为 0. 的 array

np.zeros ((3,4))

array([[ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.],
       [ 0.,  0.,  0.,  0.]])

　ones

　　生成一个三维的 array,通过 dtype 指定类型

np.ones( (2,3,4), dtype=np.int32 )

array([[[1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1]],

       [[1, 1, 1, 1],
        [1, 1, 1, 1],
        [1, 1, 1, 1]]])

　arange

　　指定范围和数值间的间隔生成 array，注意范围包左不包右 

np.arange(0,10,2)

array([0, 2, 4, 6, 8])

　linespace 随机数

　　生成等差数列

>>> np.linspace(0,10)        # 默认生成50个值
array([ 0.        ,  0.20408163,  0.40816327,  0.6122449 ,  0.81632653,
        1.02040816,  1.2244898 ,  1.42857143,  1.63265306,  1.83673469,
        2.04081633,  2.24489796,  2.44897959,  2.65306122,  2.85714286,
        3.06122449,  3.26530612,  3.46938776,  3.67346939,  3.87755102,
        4.08163265,  4.28571429,  4.48979592,  4.69387755,  4.89795918,
        5.10204082,  5.30612245,  5.51020408,  5.71428571,  5.91836735,
        6.12244898,  6.32653061,  6.53061224,  6.73469388,  6.93877551,
        7.14285714,  7.34693878,  7.55102041,  7.75510204,  7.95918367,
        8.16326531,  8.36734694,  8.57142857,  8.7755102 ,  8.97959184,
        9.18367347,  9.3877551 ,  9.59183673,  9.79591837, 10.        ])
>>> np.linspace(1,20,10,dtype=int) 可指定区间范围，个数，和类型
array([ 1,  3,  5,  7,  9, 11, 13, 15, 17, 20])

　random 随机数

　　生成指定结构的随机数，可以用于生成随机权重，用法和Python的random模块基本一致 

np.random.random((2,3))

array([[ 0.86166627,  0.37756207,  0.94265883],
       [ 0.9768257 ,  0.96915312,  0.33495431]])

>>> li = list(range(0,10))
>>> li
[0, 1, 2, 3, 4, 5, 6, 7, 8, 9]
>>> np.random.shuffle(li)  
>>> li
[5, 6, 8, 2, 1, 3, 9, 4, 0, 7]
>>> np.random.choice(li)
2
>>> np.random.sample(3)
array([0.41578646, 0.4275044 , 0.46925681])
>>> np.random.choice(5,2)
array([4, 4])
>>> np.random.choice(li,5)
array([3, 3, 4, 5, 0])
>>> np.random.rand()  # 0-1随机数
0.5526940210685204
>>> np.random.randn() # 标准正态分布
-1.3879406767054916
>>> np.random.rand(4,2)
array([[0.76781829, 0.98909192],
       [0.56726061, 0.48113612],
       [0.52529073, 0.00218226],
       [0.5546019 , 0.29870287]])
>>> np.random.randn(4,2)
array([[-0.68062491,  0.46315132],
       [-0.13610026, -0.72371849],
       [-1.15933349, -0.92001229],
       [ 0.79173944, -1.29063009]])
>>> np.random.randint(4)  # 随机整数
1
>>> np.random.randint(0,10,4)   # 0-10的随机整数
array([6, 9, 1, 1])

>>> np.random.seed(3)
>>> np.random.random()
0.5507979025745755
>>> np.random.random()
0.7081478226181048
>>> np.random.seed(3)
>>> np.random.random()
0.5507979025745755

 

五、ndarray 运算

　　元素之间依次相减相减

a = np.array([10,20,30,40])
b = np.array(4)

a - b
array([ 6, 16, 26, 36])

　　乘方

a**2
array([ 100,  400,  900, 1600])

　　开根号

np.sqrt(B)

array([[ 1.41421356,  0.        ],
       [ 1.73205081,  2.        ]])

　　e 求方

np.exp(B)

array([[  7.3890561 ,   1.        ],
       [ 20.08553692,  54.59815003]])

　　向下取整

a = np.floor(10*np.random.random((2,2)))
a

array([[ 0.,  0.],
       [ 3.,  6.]])

　　行列变换

a.T

array([[ 0.,  3.],
       [ 0.,  6.]])

　　变换结构

a.resize(1,4)
a

array([[ 0.,  0.,  3.,  6.]])

六、 矩阵运算

　　矩阵之间的运算

A = np.array( [[1,1],
               [0,1]] )
B = np.array( [[2,0],
               [3,4]] )

　　*运算

　　对于ndarray, * 作用的是进行element-wise乘积，必要时需要broadcast，作用同np.multipy

>>> a = np.array(range(6)).reshape((2,3))

>>> b = np.array([1,0,1])

>>> a

array([[0, 1, 2], [3, 4, 5]])

>>> b

array([1, 0, 1])

>>> c= a*b

>>> c

array([[0, 0, 2], [3, 0, 5]])

>>> d = a*b.T

>>> d

array([[0, 0, 2], [3, 0, 5]])

 　　而对于matrix，* 则表示矩阵相乘，运算必须保证矩阵相乘的法则:

>>> A=np.matrix(a)
>>> B=np.matrix(b)
>>> A
matrix([[0, 1, 2],
        [3, 4, 5]])
>>> B
matrix([[1, 0, 1]])
>>> C=A*B
ValueError: shapes (2,3) and (1,3) not aligned: 3 (dim 1) != 1 (dim 0)
#维数不匹配
>>> C=A*B.T
>>> C
matrix([[2],
        [8]])

　　dot运算

• 如果 a 和 b都是 1-D arrays,它的作用是计算内积。(不进行复共轭)

>>> np.dot(3, 4)
12
>>> np.dot([2j, 3+3j], [2j, 3j])
(-13+9j)

• 如果 a 和 b 是 2-D arrays, 作用是矩阵的乘积， a 和 b的维数要满足矩阵乘积维数要求，此时推荐使用 matmul 或 a @ b 。

>>> a = [[1, 0], [0, 1]]
>>> b = [[4, 1], [2, 2]]
>>> np.dot(a, b)
array([[4, 1],
       [2, 2]])

• 如果 a 或 b 是 0-D (标量), 等价于 multiply ，推荐使用 numpy.multiply(a, b)或 a * b。　　

• 如果 a 是 N-D array 且 b 是 1-D array， 作用是在a 和 b的最后一个轴上进行sum product运算。

>>> a = array([[[ 1.,  2.,  3.,  4.],
          [ 5.,  6.,  7.,  8.],
          [ 9., 10., 11., 12.]],

         [[ 1.,  2.,  3.,  4.],
          [ 5.,  6.,  7.,  8.],
          [ 9., 10., 11., 12.]]])
>>> b = np.array([1,2,3,4])
>>>np.dot(a, b)

array([[ 30.,  70., 110.],
       [ 30.,  70., 110.]])

• 如果a 是 N-D array 且 b 是 M-D array (M>=2), 作用是在a的最后一个轴上和b的倒数第二个轴上进行sum product，即 :

dot(a, b)[i,j,k,m] = sum(a[i,j,:] * b[k,:,m])

>>> a = np.arange(3*4*5*6).reshape((3,4,5,6))
>>> b = np.arange(3*4*5*6)[::-1].reshape((5,4,6,3))
>>> np.dot(a, b)[2,3,2,1,2,2]
499128
>>> sum(a[2,3,2,:] * b[1,2,:,2])
499128

　　

　　multiply运算

　　函数原型是

numpy.multiply(x1, x2, /, out=None, *, where=True, casting='same_kind', order='K', dtype=None, subok=True[, signature, extobj]) = <ufunc 'multiply'>

　　Returns:
　　　　y : ndarray
　　　　x1 和 x2的element-wise乘积，保证x1和x2有相同的维数，或者进行broadcast之后两者有相同的维数

>>> np.multiply(2.0, 4.0)
8.0

>>> x1 = np.arange(9.0).reshape((3, 3))
>>> x2 = np.arange(3.0)
>>> np.multiply(x1, x2)
array([[  0.,   1.,   4.],
       [  0.,   4.,  10.],
       [  0.,   7.,  16.]])
#要进行broadcast

　　

　　横向堆叠

a = np.floor(10*np.random.random((2,2)))
b = np.floor(10*np.random.random((2,2)))

print(a)
print(b)
print(np.hstack((a,b)))

[[ 2.  3.]
 [ 9.  3.]]
[[ 8.  1.]
 [ 0.  0.]]
[[ 2.  3.  8.  1.]
 [ 9.  3.  0.  0.]]

　　纵向堆叠

print(np.vstack((a,b)))

[[ 2.  3.]
 [ 9.  3.]
 [ 8.  1.]
 [ 0.  0.]]

　　矩阵分割

#横向分割
print( np.hsplit(a,3))
#纵向风格
print(np.vsplit(a,3))

七、 复制的区别

　　地址复制

　　通过 b = a 复制 a 的值，b 与 a 指向同一地址，改变 b 同时也改变 a。

a = np.arange(12)
b = a
print(a is b)

print(a.shape)
print(b.shape)
b.shape = (3,4)
print(a.shape)
print(b.shape)

True
(12,)
(12,)
(3, 4)
(3, 4)

　　复制值

　　通过 a.view() 仅复制值，当对 c 值进行改变会改变 a 的对应的值，而改变 c 的 shape 不改变 a 的 shape

a = np.arange(12)
c = a.view()
print(c is a)

c.shape = 2,6
c[0,0] = 9999

print(a)
print(c)

False
[9999    1    2    3    4    5    6    7    8    9   10   11]
[[9999    1    2    3    4    5]
 [   6    7    8    9   10   11]]

　完整拷贝

　　a.copy() 进行的完整的拷贝，产生一份完全相同的独立的复制

 

a = np.arange(12)
c = a.copy()
print(c is a)

c.shape = 2,6
c[0,0] = 9999

print(a)
print(c)

False
[ 0  1  2  3  4  5  6  7  8  9 10 11]
[[9999    1    2    3    4    5]
 [   6    7    8    9   10   11]]

 八、数组的排序

　　经常需要对数组或者list进行排序，python提供了好几种排序的函数，下面说明下特点：

In [98]: a = np.array([[2,4,1],[4,3,9]])

In [99]: a
Out[99]: 
array([[2, 4, 1],
       [4, 3, 9]])

　　1、ndarray.sort(axis=-1,kind='quicksort',order=None)

• 使用方法：a.sort
• 参数说明：
• axis：排序沿着数组的方向，0表示按行，1表示按列
• kind：排序的算法，提供了快排、混排、堆排
• order：不是指的顺序，以后用的时候再去分析这个
• 作用效果：对数组a排序，排序后直接改变了a

In [101]: a.sort(axis=1)

In [102]: a
Out[102]: 
array([[1, 2, 4],
       [3, 4, 9]])

　　2、numpy.sort(a,axis=-1,kind='quicksort',order=None)

• 使用方法：numpy.sort(a)
• 参数说明：
• a：要排序的数组，其他同1
• 作用效果：对数组a排序，返回一个排序后的数组（与a相同维度），a不变

In [106]: np.sort(a,axis=1)
Out[106]: 
array([[1, 2, 4],
       [3, 4, 9]])

In [107]: a
Out[107]: 
array([[2, 4, 1],
       [4, 3, 9]])

　　3、numpy.argsort(a,axis=-1,kind='quicksort',order=None)，numpy.argsort() 和 numpy.lexsort()都可以返回升序排序后的索引，不同的是numpy.lexsort() 可以接受多列，即可以进行子排序。

• 使用方法：numpy.argsort(a)
• 参数说明：同2
• 作用效果：对数组a排序，返回一个排序后索引，a不变

In [108]: np.argsort(a,axis=1)
Out[108]: 
array([[2, 0, 1],
       [1, 0, 2]])

In [109]: a
Out[109]: 
array([[2, 4, 1],
       [4, 3, 9]])

　　4、python 内置函数 sorted(iterable,cmp=None,key=None,reverse=False)

• 说明：内置的排序函数，对list，字典等等可以使用
• iterable：是可迭代类型;
• cmp：用于比较的函数，比较什么由key决定,有默认值，迭代集合中的一项;
• key：用列表元素的某个属性和函数进行作为关键字，有默认值，迭代集合中的一项;
• reverse：排序规则.reverse=True或者reverse=False，默认False（从小到大）。
• 返回值：是一个经过排序的可迭代类型，与iterable一样;

In [112]: sorted(a[0])
Out[112]: [1, 2, 4]