算法(一)

算法的时间复杂度

算法时间复杂度用来度量算法执行时间的多少，用T(n)=O(f(n))，其中n为问题规模，也就是问题的大小。

# 时间复杂度，用来估算算法运行效率的

print("hello world") # T(n) = O(1)


for i in range(n):    
    print("hello world")    # T(n) = O(n)
    
    
for i in range(n):
    for j in range(n):
        print("hello world")   # T(n) = O(n**2)
        
        
for i in range(n):
    for j in range(n):
        for k in range(n):
            print("hello world") # T(n) = O(n**3)


# T(n) = O(log n)
def foo(n):
    while n >1:
        print(n)
        n = n //2
foo(64)

常见的时间复杂度
O(1) < O(logn) < O(n) < O(nlogn) < O(n2) < O(n2logn) < O(n3)

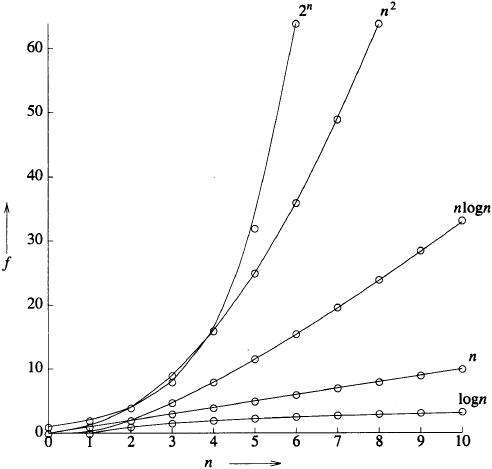
简单判断时间复杂度的方法
1.有循环减半的过程 O(log n)

2.几次循环就是n的几次方 O(n**n)

空间复杂度

空间复杂度：用来评估算法内存占用大小的一个式子

1.程序只有变量
S(n) = O(1)

2.程序需要一个一维数组
S(n) = O(n)

3.程序有一个二维数组
S(n) = O(n2)
一般情况下，会用空间复杂度，换取时间复杂度

二分法查找

li = list(range(100000))


#  二分法查找
def bin_search(li, num):
    high = len(li)-1
    low = 0
    while high >= low:
        mid = (high + low) // 2
        if li[mid] == num:
            return mid
        elif li[mid] > num:
            high = mid -1
        else:
            low = mid + 1
    return None

# 尾递归二分法查找
def bin_search2(li, num, low, high):

    if low <= high:
        mid = (low + high) // 2
        if li[mid] == num:
            return mid
        elif li[mid] >= num:
            bin_search2(li, num, low, mid-1)
        else:
            bin_search2(li, num, low+1, high)
    else:
        return

二分法示例

# 1.二分法查找相同数
# Given an array of integers sorted in ascending order, find the starting and ending position of a given target value.

# Your algorithm's runtime complexity must be in the order of O(log n).

# If the target is not found in the array, return [-1, -1].

# For example,
# Given [5, 7, 7, 8, 8, 10] and target value 8,
# return [3, 4].
def bin_search(li, target):
    # 先利用二分法，匹配到mid。
    # 开两个for循环，依次从mid往左和往右查找，直到第一个不等于TARGET的时候返回
    low = 0
    high = len(li) - 1
    while low <= high:
        mid = (low + high) // 2
        if li[mid] == target:
            a = mid
            b = mid
            while li[a] == target and a >= 0:  # and 条件在最开始
                a -= 1
            while li[b] == target and b < len(li) - 1:
                b += 1
            return (a + 1, b)

        elif li[mid] > target:
            high = mid - 1
        else:
            low = mid + 1
    return None


print(bin_search([1, 1, 3, 5, 6, 7, 8, 9, 10, 10], 10))

# 2.
# Given an array of integers,
# return indices of the two numbers such that they add up to a specific target.
# You may assume that each input would have exactly one solution,
# and you may not use the same element twice.

# Example
# Given nums = [2, 7, 11, 15], target = 9,

# Because nums[0] + nums[1] = 2 + 7 = 9,
# return [0, 1].

nums = [2, 7, 11, 15]


def twoSum(nums, target):
    '''
    时间复杂度O(N**2), 两层循环，依次匹配
    :param nums: 
    :param target: 
    :return: 
    '''
    for i in range(len(nums)):
        for j in range(i + 1, len(nums)):
            if nums[i] + nums[j] == target:
                return i, j

    return None


# print(twoSum(nums, 18))


def tow_sum_2(nums, target):


# TODO：fOr 循环固定单个值， 用target - 固定值， 用二分法查待匹配的值。


def two_sum_3(nums, target):
    # 列表有序，初始值 Sum = Num[low]+Num[high]
    # 从最左和最右移动索

    low = 0
    high = len(nums) - 1
    while low < high:
        sum = nums[low] + nums[high]  # 列表有序，初始 sum = 列表最小值+最大值
        if sum > target:
            high -= 1
        elif sum < target:
            low += 1
        else:
            return low, high
    return -1, -1


print(two_sum_3(nums, 22))


# TODO：尝试目标值由三个数相加得来，返回三个下标。