题目链接:https://vjudge.net/problem/HDU-6222
思路:打表找规律。
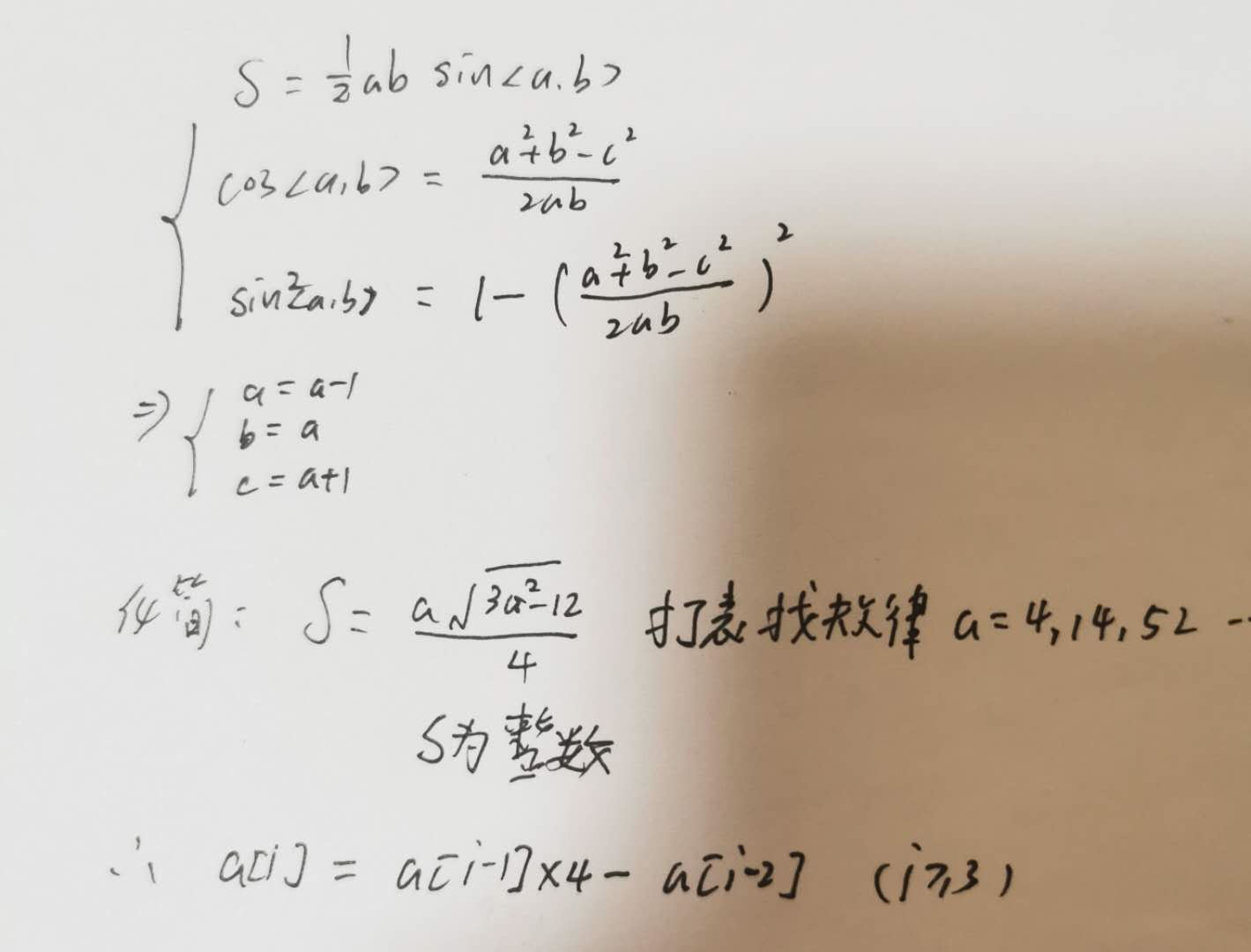
然后因为数据范围较大可以考虑用字符串模拟,或者__int128要注意用一个快读快输模板。
1 #include <bits/stdc++.h> 2 #include <time.h> 3 #include <set> 4 #include <map> 5 #include <stack> 6 #include <cmath> 7 #include <queue> 8 #include <cstdio> 9 #include <string> 10 #include <vector> 11 #include <cstring> 12 #include <utility> 13 #include <cstring> 14 #include <iostream> 15 #include <algorithm> 16 #include <list> 17 using namespace std; 18 //cout<<setprecision(10)<<fixed; 19 #define eps 1e-6 20 #define PI acos(-1.0) 21 #define lowbit(x) ((x)&(-x)) 22 #define zero(x) (((x)>0?(x):-(x))<eps) 23 #define mem(s,n) memset(s,n,sizeof s); 24 #define rep(i,a,b) for(int i=a;i<=b;i++) 25 #define rep2(i,a,b) for(int i=a;i>=b;i--) 26 #define ios {ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);} 27 typedef long long ll; 28 typedef unsigned long long ull; 29 const int maxn=1e6+5; 30 const ll Inf=0x7f7f7f7f7f7f7f7f; 31 const ll mod=1e9; 32 //const int N=3e3+5; 33 bool isPowerOfTwo(int n) { return n > 0 && (n & (n - 1)) == 0; }//判断一个数是不是 2 的正整数次幂 34 int modPowerOfTwo(int x, int mod) { return x & (mod - 1); }//对 2 的非负整数次幂取模 35 int getBit(int a, int b) { return (a >> b) & 1; }// 获取 a 的第 b 位,最低位编号为 0 36 int Max(int a, int b) { return b & ((a - b) >> 31) | a & (~(a - b) >> 31); }// 如果 a>=b,(a-b)>>31 为 0,否则为 -1 37 int Min(int a, int b) { return a & ((a - b) >> 31) | b & (~(a - b) >> 31); } 38 ll gcd(ll a, ll b) {return b ? gcd(b, a % b) : a;} 39 ll lcm(ll a, ll b) {return a / gcd(a, b) * b;} 40 inline int read() 41 { 42 int X=0; bool flag=1; char ch=getchar(); 43 while(ch<'0'||ch>'9') {if(ch=='-') flag=0; ch=getchar();} 44 while(ch>='0'&&ch<='9') {X=(X<<1)+(X<<3)+ch-'0'; ch=getchar();} 45 if(flag) return X; 46 return ~(X-1); 47 } 48 inline void write(int X) 49 { 50 if(X<0) {X=~(X-1); putchar('-');} 51 if(X>9) write(X/10); 52 putchar(X%10+'0'); 53 } 54 /* 55 inline int write(int X) 56 { 57 if(X<0) {putchar('-'); X=~(X-1);} 58 int s[20],top=0; 59 while(X) {s[++top]=X%10; X/=10;} 60 if(!top) s[++top]=0; 61 while(top) putchar(s[top--]+'0'); 62 } 63 */ 64 int Abs(int n) { 65 return (n ^ (n >> 31)) - (n >> 31); 66 /* n>>31 取得 n 的符号,若 n 为正数,n>>31 等于 0,若 n 为负数,n>>31 等于 -1 67 若 n 为正数 n^0=n, 数不变,若 n 为负数有 n^(-1) 68 需要计算 n 和 -1 的补码,然后进行异或运算, 69 结果 n 变号并且为 n 的绝对值减 1,再减去 -1 就是绝对值 */ 70 } 71 ll binpow(ll a, ll b) { 72 ll res = 1; 73 while (b > 0) { 74 if (b & 1) res = res * a%mod; 75 a = a * a%mod; 76 b >>= 1; 77 } 78 return res%mod; 79 } 80 void extend_gcd(ll a,ll b,ll &x,ll &y) 81 { 82 if(b==0) { 83 x=1,y=0; 84 return; 85 } 86 extend_gcd(b,a%b,x,y); 87 ll tmp=x; 88 x=y; 89 y=tmp-(a/b)*y; 90 } 91 ll mod_inverse(ll a,ll m) 92 { 93 ll x,y; 94 extend_gcd(a,m,x,y); 95 return (m+x%m)%m; 96 } 97 ll eulor(ll x) 98 { 99 ll cnt=x; 100 ll ma=sqrt(x); 101 for(int i=2;i<=ma;i++) 102 { 103 if(x%i==0) cnt=cnt/i*(i-1); 104 while(x%i==0) x/=i; 105 } 106 if(x>1) cnt=cnt/x*(x-1); 107 return cnt; 108 } 109 void scan(__int128 &x)//输入 110 { 111 x = 0; 112 int f = 1; 113 char ch; 114 if((ch = getchar()) == '-') f = -f; 115 else x = x*10 + ch-'0'; 116 while((ch = getchar()) >= '0' && ch <= '9') 117 x = x*10 + ch-'0'; 118 x *= f; 119 } 120 void _print(__int128 x) 121 { 122 if(x > 9) _print(x/10); 123 putchar(x%10 + '0'); 124 } 125 __int128 a[maxn]; 126 int main() 127 { 128 int t=read(); 129 a[1]=4; 130 a[2]=14; 131 __int128 b=1e31; 132 int i; 133 for( i=3;;i++) 134 { 135 a[i]=a[i-1]*4-a[i-2]; 136 if(a[i]>b) break; 137 } 138 while(t--) 139 { 140 __int128 n; 141 scan(n); 142 for(int j=1;j<=i;j++) 143 { 144 if(a[j]>=n) {_print(a[j]);puts("");break;} 145 } 146 } 147 return 0; 148 }