USACO2007 The Bale Tower /// DFS oj21160

题目大意：

给出N个捆包，每个捆包有相应的长度和宽度，要求堆叠捆包，使下方的捆包长宽永远大于上方的捆包的长宽。

 

Input

Multiple test case. For each case:

* Line 1: A single integer, N

* Lines 2..N+1: Each line describes a bale with two space-separated integers, respectively the width and breadth

Output

For each case, output one line: The height of the tallest possible tower that can legally be built from the bales.

Sample Input

6
6 9
10 12
9 11
8 10
7 8
5 3

Sample Output

5

方法一

先结构体sort()对长排序 长相等时对宽排序， 再枚举各个宽为底，算出所有可能结果，再求出最大结果

#include <bits/stdc++.h>
using namespace std;
int n,ans;
struct BALE
{
    int x,y;
}bale[25];
bool cmp(struct BALE q,struct BALE p)
{
    if(q.x==p.x) return q.y<p.x;
    return q.x>p.x;
}
void cnt(int i,int sum)
{
    ans=max(ans,sum);
    if(sum==n) return;
    for(int j=i+1;j<n;j++)
        if(bale[i].y>=bale[j].y)
        {
            cnt(j,sum+1);
            if(sum==n) return;
        }
}
int main()
{
    while(~scanf("%d",&n))
    {
        ans=0;
        for(int i=0;i<n;i++)
            scanf("%d%d",&bale[i].x,&bale[i].y);
        sort(bale,bale+n,cmp);
        for(int i=0;i<n;i++)
        {
            cnt(i,1);
            //printf("%d
",cnt(i));
        }
        printf("%d
",ans);
    }

    return 0;
}

—— 01.28更 ——

OJ测试数据更新了之后 这份代码狗带了 因为相同的情况是不能考虑的 

如：

3

9  3

8  4

8  4

答案应为  1

按方法二补

#include <bits/stdc++.h>
using namespace std;
int n,ans,flag[25];
struct BALE
{
    int x,y;
}bale[25];
void DFS(int i,int sum)
{
    ans=max(sum,ans);
    if(sum==n) return;
    for(int j=1;j<=n;j++)
    {
        if(bale[i].x>bale[j].x&&bale[i].y>bale[j].y&&!flag[j])
        {
            flag[j]=1;
            DFS(j,sum+1);
            flag[j]=0;
        }
    }
}
int main()
{
    while(~scanf("%d",&n))
    {
        ans=0;
        for(int i=1;i<=n;i++)
            scanf("%d%d",&bale[i].x,&bale[i].y);
        for(int i=1;i<=n;i++)
        {
            memset(flag,0,sizeof(flag));
            flag[i]=1;
            DFS(i,1);
        }
        printf("%d
",ans);
    }

    return 0;
}

————————

方法二

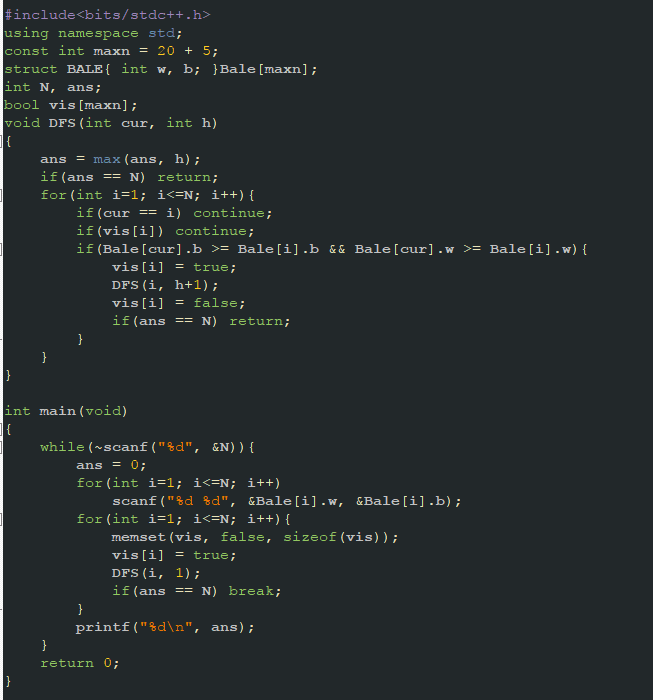
DFS深搜  （偷下LXH的代码）

还是需要添加标记