传统旋转电机想要实现直线运动,需要配合滚珠丝杠结构:限制了运动行程、结构刚度有限、传统过程中损耗大、速度和加速度低。
一、电机结构
图1.1为感应电动机,将其沿径向剖开并拉直得到图1.2的原始直线电机。由定子演变而来的一侧成为初级或原边,由转子演变而来的一边成为次极或副边。
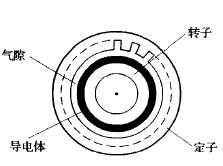
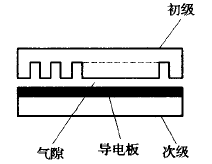
图 1.1 普通旋转电机 图 1.2 最原始的直线感应电机
现将三相交流电通入图1.2初级三相绕组上,气隙中产生直线移动的磁场,次极感应电流与磁场相互作用产生电磁推力,次极沿着磁场移动方向做直线运动。通常情况下,原始直线电机不满足电机运行需求,常采用延长次极或初级的方式进行结构改进。
结论:旋转电机与直线电机基本原理相同,结构有所差异。
二、直线电机
直线电机两端开断结构的存在,使之具有旋转电机没有的独特现象和问题。
- 初级电流固有不平衡:
互感不相等引起的电流不平衡
- 纵向端面磁通:
由于直线电机铁心开断,磁力线从下端铁心端面到达上铁心两个端面,经气隙闭合,如图2.1所示。
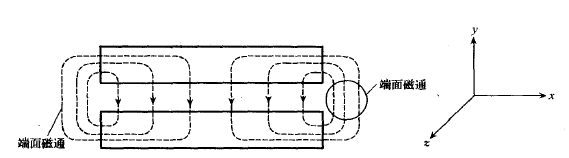
图 2.1 纵向端面磁通
- 电瞬态现象:
次极在入端处磁场变化,感生瞬态电流,使的气隙磁场减小,又称“纵向动态端部效应”。
- 绕组特点和“半填充槽”:
旋转电机剖开、展开成为直线电机,要求初级绕组改变,结构形式主要有图2.2和图2.3两种。

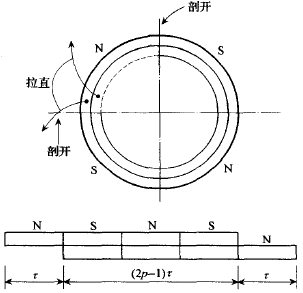
图 2.2 偶数极直线电机 图 2.3 奇数极半填充端部槽直线电机
- 垂直力问题
三、初级绕组串并联
绕组采用串、并联连接,电机阻抗(电压与电流比)不同。
1.初级绕组串联
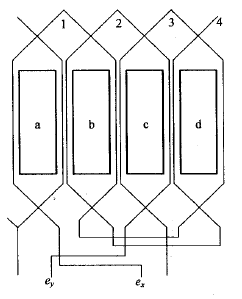
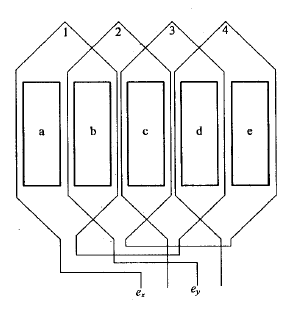
图 3.1 二相二极旋转电机初级绕组串联展开 图 3.2 二相二极直线电机初级绕组串联展开
以二相二极电机旋转电机(图3.1)为例,分析初级绕组串、并联对于电机性能影响的步骤:
Step1.忽略初级绕组电阻和漏抗,得到电压方程
$\frac{d}{d t}\left(\phi_{a}+\phi_{b}-\phi_{c}-\phi_{d}\right)=e_{x}$
$\frac{d}{d t}\left(\phi_{b}+\phi_{c}-\phi_{d}-\phi_{a}\right)=e_{y}$
其中,$\phi_{a}, \phi_{b}, \phi_{c}, \phi_{d}$为通过齿a、b、c、d的磁通。
Step2.得到磁路方程
$\phi_{\mathrm{a} 1}+\phi_{\mathrm{b} 1}=k i_{\mathrm{x}}$
$-\left(\phi_{\mathrm{c} 1}+\phi_{\mathrm{d} 1}\right)=k i_{x}$
其中,$\phi_{a i}, \phi_{b i}, \phi_{c i}, \phi_{d i}$为线圈i的磁势再齿a、b、c、d中产生的磁通;
k为磁路常数(由气隙和其他尺寸决定)。
Step3.求线圈共同作用在不同齿中的磁通
因为$\phi_{a 1}=\phi_{b 1}, \phi_{c 1}=\phi_{d 1}, \phi_{b 2}=\phi_{c 2}, \phi_{a 2}=\phi_{d 2}, \phi_{c 3}=\phi_{d 3}, \phi_{a 3}=\phi_{b 3}, \phi_{d 4}=\phi_{a 4},\phi_{b 4}=\phi_{c 4}$
$\phi_{a}=\phi_{a 1}+\phi_{a 2}+\phi_{a 3}+\phi_{a 4}=k\left(i_{x}-i_{y}\right)$
$\phi_{b}=\phi_{b 1}+\phi_{b 2}+\phi_{b 3}+\phi_{b 4}=k\left(i_{x}+i_{y}\right)$
}+\phi_{c 2}+\phi_{c 3}+\phi_{c 4}=k\left(-i_{x}+i_{y}\right)$
$\phi_{d}=\phi_{d 1}+\phi_{d 2}+\phi_{d 3}+\phi_{d 4}=k\left(-i_{x}-i_{y}\right)$
Step4.将步骤3中计算得到的磁通带入步骤1
$\frac{\mathrm{d} i_{x}}{\mathrm{d} t}=\frac{1}{4 k} e_{x}$ $\frac{\mathrm{d} i_{y}}{\mathrm{d} t}=\frac{1}{4 k} e_{y}$
$\frac{\mathrm{d} \phi_{\mathrm{a}}}{\mathrm{d} t}=\frac{1}{4}\left(e_{x}-e_{y}\right)$
$\frac{\mathrm{d} \phi_{\mathrm{b}}}{\mathrm{d} t}=\frac{1}{4}\left(e_{x}+e_{y}\right)$
$\frac{\mathrm{d} \phi_{\mathrm{c}}}{\mathrm{d} t}=\frac{1}{4}\left(-e_{x}+e_{y}\right)$
$\frac{\mathrm{d} \phi_{\mathrm{d}}}{\mathrm{d} t}=-\frac{1}{4}\left(e_{x}+e_{y}\right)$
Step5.对时间积分,得到电压、电流、磁通的向量关系,如图3.3所示
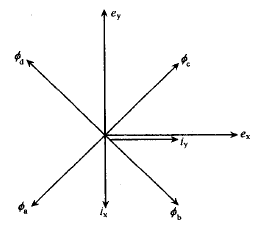
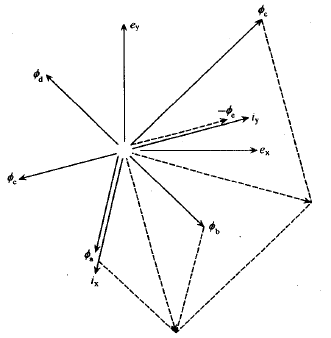
图 3.3 旋转电机绕组串联电流、磁通向量图 图 3.4 直线电机绕组串联电流、磁通向量图
直线电机与旋转电机计算不同之处在于:在图3.2中,线圈1产生的磁通由齿a、b发出经过气隙到达次极,再通过气隙回到齿c、d、e形成闭合回路。回路的长度相等、面积不同(2:3)的空气隙串联组成,它的磁导相对于3.1来说增加到1.2倍,由此将步骤2中的磁路方程修改如下。
$\phi_{\mathrm{a} 1}+\phi_{\mathrm{b} 1}=\frac{6}{5} k i_{x} ; \quad \phi_{\mathrm{cl}}+\phi_{\mathrm{d} 1}+\phi_{e 1}=-\frac{6}{5} k i_{x}$
$\phi_{\mathrm{b} 2}+\phi_{\mathrm{c} 2}=\frac{6}{5} k i_{\mathrm{y}} ; \quad \phi_{\mathrm{d} 2}+\phi_{\mathrm{e} 2}+\phi_{a 2}=-\frac{6}{5} k i_{\mathrm{y}}$
$\phi_{c 3}+\phi_{\mathrm{d} 3}=-\frac{6}{5} k i_{x} ; \quad \phi_{\mathrm{e} 3}+\phi_{\mathrm{a} 3}+\phi_{\mathrm{b} 3}=\frac{6}{5} k i_{x}$
$\phi_{d 4}+\phi_{e 4}=-\frac{6}{5} k i_{y} ; \quad \phi_{a 4}+\phi_{\mathrm{b} 4}+\phi_{\mathrm{c 4}}=\frac{6}{5} k i_{\mathrm{y}}$
式中,
$\phi_{\mathrm{a} 1}=\phi_{\mathrm{b} 1} ; \phi_{\mathrm{b} 2}=\phi_{\mathrm{c} 2} ; \phi_{\mathrm{c} 3}=\phi_{\mathrm{d} 3} ; \phi_{\mathrm{d} 4}=\phi_{\mathrm{e} 4}$
$\phi_{\mathrm{c} 1}=\phi_{\mathrm{e} 1}=\phi_{\mathrm{e} 1} ; \phi_{\mathrm{d} 2}=\phi_{\mathrm{e} 2}=\phi_{\mathrm{a} 2} ; \phi_{\mathrm{e} 3}=\phi_{\mathrm{a} 3}=\phi_{\mathrm{b} 3} ; \phi_{\mathrm{a 4}}=\phi_{\mathrm{b} 4}=\phi_{\mathrm{c} 4}$
其余步骤相同,最终得到向量图3.4。
2.初级绕组并联
对于旋转电机,磁路和电路对称。与串联相比,除了电压、电流比不同,电机内部电流和磁场都一样。因此,并联时电机的性能与串联时完全相同。
下面以二相二级电机为例,对初级绕组并联的感应直线电机进行分析,图3.5为二相二级直线感应电动机初级绕组并联展开图。
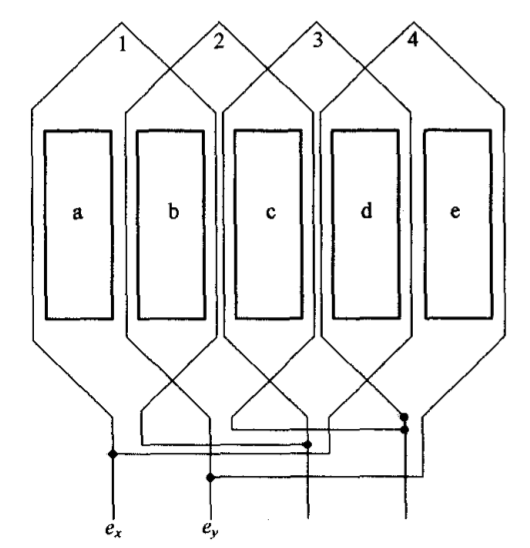
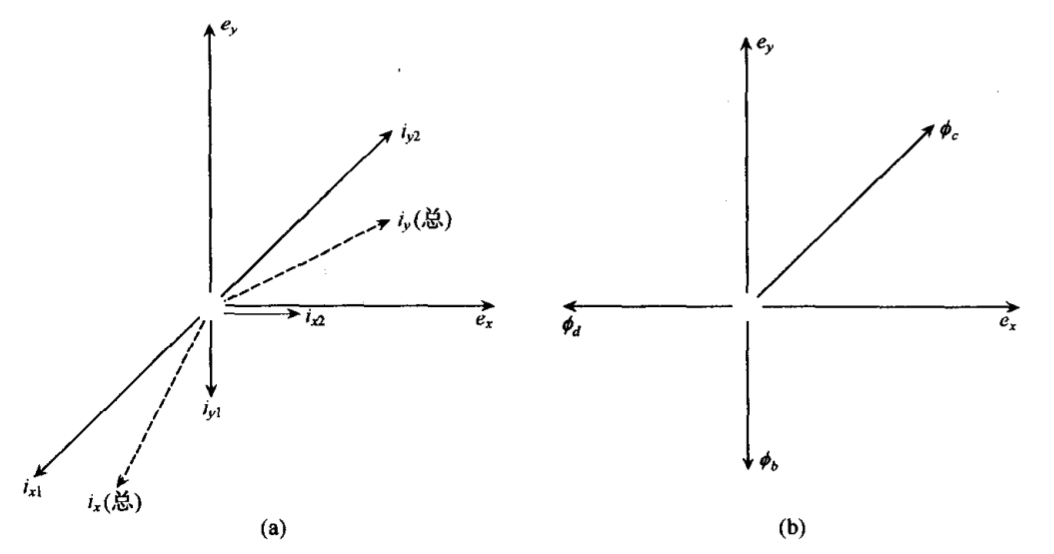
图 3.5 直线电机初级绕组并联展开图 图 3.6 直线电机绕组并联电流和磁通矢量图
Step1.四个线圈的电压方程
$$
\begin{array}{c}{\frac{\mathrm{d}}{\mathrm{d} t}\left(\phi_{\mathrm{a}}+\phi_{\mathrm{b}}\right)=e_{x}} \\ {\frac{\mathrm{d}}{\mathrm{d} t}\left(\phi_{\mathrm{b}}+\phi_{\mathrm{c}}\right)=e_{\mathrm{y}}} \\ {\frac{\mathrm{d}}{\mathrm{d} t}\left(-\phi_{\mathrm{c}}-\phi_{\mathrm{d}}\right)=e_{x}} \\ {\frac{\mathrm{d}}{\mathrm{d} t}\left(-\phi_{\mathrm{d}}-\phi_{\mathrm{e}}\right)=e_{y}}\end{array}
$$
Step2.写出四个线圈磁路方程
$$
\phi_{\mathrm{a} 1}+\phi_{\mathrm{b} 1}=\frac{6}{5} k i_{x 1} ;-\left(\phi_{\mathrm{c} 1}+\phi_{\mathrm{d} 1}+\phi_{\mathrm{e} 1}\right)=\frac{6}{5} k i_{x_{1}}
$$
2.3.4线圈同理
Step3.推导五个齿中磁通
$$
\phi_{\mathrm{a} 1}=\phi_{\mathrm{b} 1} ; \phi_{\mathrm{b} 2}=\phi_{\mathrm{c} 2} ; \phi_{\mathrm{c} 3}=\phi_{\mathrm{d} 3} ; \phi_{\mathrm{d} 4}=\phi_{\mathrm{e4}}
$$
$$
\(\phi_{\mathrm{c1}}=\phi_{\mathrm{d} 1}=\phi_{\mathrm{e1}} ; \phi_{\mathrm{d} 2}=\phi_{\mathrm{e} 2} =\phi_{\mathrm{a} 2}; \phi_{\mathrm{e} 3}=\phi_{\mathrm{a3}}=\phi_{\mathrm{b} 3} ; \phi_{\mathrm{a4}}=\phi_{\mathrm{b} 4}=\phi_{\mathrm{c} 4}\)
$$
因此
$$
\phi_{\mathrm{a1}}=\frac{3}{5} k i_{x 1} ; \phi_{\mathrm{a} 2}=-\frac{2}{5} k i_{y 1} ; \phi_{\mathrm{a3}}=\frac{2}{5} k i_{x 2} ; \phi_{\mathrm{a4}}=\frac{2}{5} k i_{y 2}
$$
1、2、3、4线圈在b、c、d、e齿产生的磁通同理
于是有
$$
\phi_{\mathrm{a}}=\Sigma \phi_{\mathrm{ai}}=\frac{6}{5} k\left(\frac{1}{2} i_{x 1}-\frac{1}{3} i_{\mathrm{y} 1}+\frac{1}{3} i_{x 2}+\frac{1}{3} i_{\mathrm{y2}}\right)
$$
Step4.将步骤3中计算得到的磁通带入步骤1
$$
\begin{aligned}
&\frac{\mathrm{d} i_{x 1}}{\mathrm{d} t}=\frac{2}{k}\left(e_{x}-e_{y}\right) ; \quad \frac{\mathrm{d} i_{y 1}}{\mathrm{d} t}=\frac{1}{k} e_{x}\\
&\frac{\mathrm{d} i_{x 2}}{\mathrm{d} t}=\frac{1}{k} e_{y} ; \quad \frac{\mathrm{d} i_{y 2}}{\mathrm{d} t}=\frac{2}{k}\left(e_{y}-e_{x}\right)
\end{aligned}
$$
结论:
- 旋转电机中:串、并联不影响电机性能。
- 直线电机中:串、并联影响电机性能。