回顾问题
这个数学问题来源于一个娱乐节目。节目中有一位参与者和一位主持人,在参与者的面前有三扇关闭的门,其中两扇门的后面是空的,剩下一扇门后是一辆法拉利跑车。

主持人知道哪一扇门后面有跑车,但参与者不知道。此时让参与者人选一扇门,如果选择的是后面有跑车的那扇门,跑车就作为奖励送给参与者。
问题一直到这里都很简单:一共有三扇门,参与者随机做选择,获奖几率肯定是1/3。

下面是问题的重点,当参与者进行选择以后,暂时先不打开这扇门,接下来主持人把剩下两扇门当中的一扇打开,是空门。

此时主持人给了参与者重新选择的机会:可以坚持刚才选择的门(在图中是2号门),也可以换另一扇没有打开的门(在图中是1号门)。
如果你是游戏参与者,你怎样选择的获奖率更大?获奖率又是多少?
匪夷所思的答案
刚刚看到这个问题的,也颇不以为然:
这种题还用问吗?有三扇门的时候,获奖率是1/3;现在排除了一扇门,剩下两个门二选一,换门或不换门,获奖率应该都是50%才对呀?
但是,正确答案是十分 “反直觉” 的:
换门的获奖率是 2/3
不换门的获奖率是 1/3
What's the hell?这简直是匪夷所思啊!
“当最后剩下两扇门的时候,此时讨论的获奖率应该是一个独立事件,和之前参与者怎么选择,以及主持人打开空门这些事,应该完全无关才对呀?既然是一个独立事件,那么二选一,难道获奖率不是50%吗?”
首先需要明确一点,我们讨论的关于“换门”的获奖率不是一个独立事件,必须以第一次的选择作为基础。在概率学当中,这种情况叫做条件概率。
那么,到底什么样才是独立事件呢?
举个例子,假如游戏的参与者本来是小灰,当小灰选择一扇门,而主持人打开一扇空门之后,不明真相的小红从外面跑了进来。小红并不知道当初小灰选择的是哪一扇门,只知道剩下两扇关闭的门中,有一扇门藏有奖励。
那么此时对于小红来说,无论选择哪一扇门,获奖率都是50%,因为小红是在做独立的选择,而不是基于第一次的选择来”换门”。

这才是所谓的 “独立事件”。
从多个角度来思考
那么,在“换门”的情况下,获奖率2/3又是怎么来的呢?
小灰上周的漫画里,利用了基于“贝叶斯理论”的思想来分析换与不换的获奖率:
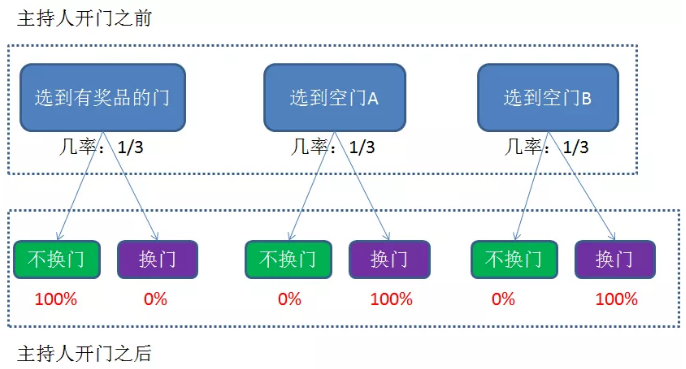
直白地讲,就是把第一次选择和第二次选择的所有情况进行细化,分析出每一种情况下的条件概率,再把这些概率进行加总,得到了最终的结果:
不换门的获奖率 = (1/3 X 100%)+(1/3 X 0%)+(1/3 X 0%)=1/3
换门的获奖率 = (1/3 X 0%)+(1/3 X 100%)+(1/3 X 100%)=2/3
用代码来验证
上面所说的都仅仅是理论分析,我们不妨用代码来实际检验一下。

1 package test; 2 3 import java.util.ArrayList; 4 import java.util.Arrays; 5 import java.util.List; 6 import java.util.Random; 7 8 /** 9 * @author zsh 10 * @site qqzsh.top 11 * @create 2019-08-02 9:28 12 * @description 三门问题 13 * 这个数学问题来源于一个娱乐节目。节目中有一位参与者和一位主持人,在参与者的面前有三扇关闭的门,其中两扇门的后面是空的,剩下一扇门后是一辆法拉利跑车。 14 * 主持人知道哪一扇门后面有跑车,但参与者不知道。此时让参与者人选一扇门,如果选择的是后面有跑车的那扇门,跑车就作为奖励送给参与者。 15 * 下面是问题的重点,当参与者进行选择以后,暂时先不打开这扇门,接下来主持人把剩下两扇门当中的一扇打开,是空门。 16 * 此时主持人给了参与者重新选择的机会:可以坚持刚才选择的门(在图中是2号门),也可以换另一扇没有打开的门(在图中是1号门)。 17 * 如果你是游戏参与者,你怎样选择的获奖率更大?获奖率又是多少? 18 */ 19 public class threeDoorsTest { 20 public static void main(String[] args) { 21 //换门的获奖总次数 22 int changeWinCount = 0; 23 //不换门的获奖总次数 24 int unChangeWinCount = 0; 25 Random random = new Random(); 26 for (int i = 0; i < 100000; i++) { 27 List<Integer> doors = new ArrayList<>(Arrays.asList(0,1,2)); 28 int bonusDoor = random.nextInt(3); 29 int selectedDoor = random.nextInt(3); 30 //主持人打开一扇空门 31 for (int j = 0; j < doors.size(); j++) { 32 if (doors.get(j) != selectedDoor && doors.get(j) != bonusDoor){ 33 doors.remove(j); 34 break; 35 } 36 } 37 //获得换门的序号,此时集合中就剩两个元素 38 int changedDoor = doors.get(0); 39 if (changedDoor == selectedDoor){ 40 changedDoor = doors.get(1); 41 } 42 //如果不换门有奖,unChangeWinCount加1;如果换门有奖,changeWinCount加1 43 if (selectedDoor == bonusDoor){ 44 unChangeWinCount++; 45 }else if (changedDoor == bonusDoor){ 46 changeWinCount++; 47 } 48 } 49 System.out.println("不换门获奖总次数:"+unChangeWinCount+",所占比例:"+(float)unChangeWinCount/100000); 50 System.out.println("换门获奖总次数:"+changeWinCount+",所占比例:"+(float)changeWinCount/100000); 51 } 52 }
运行结果:

数据结果显而易见,不换门获奖的比例占了约1/3,换门获奖的比例占了2/3。
写在最后
三门问题真的是一个非常有意思的数学问题。在上个世纪的美国,这个问题刚刚被提出的时候,也遭到过许多人的质疑,这些质疑者中有教师,有学者,甚至有数学家。后来人们经过了许多次实验,才逐渐达成共识。
质疑精神是值得鼓励的,有了质疑才能让思想进一步完善。
最后,让我们来致敬一下 “三门问题” 的提出者,集才华和美貌于一身的天才人物 玛丽莲·沃斯·莎凡特。
