2018年5月29号（堆排序最小顶）

　　今天老师讲了堆排序和有关堆的一些知识，作为蒟蒻的我，任是没有听懂；但是大佬的博客指点一下有一点感觉；

首先是堆的概念（不要着急百度，我来给你百度一下）：

1.堆的基本概念：

　　严格来讲，堆有不同的种类，但是我们在算法学习中，主要用的还是二叉堆，而二叉堆有最大堆和最小堆之分。

　　最大（最小）堆是一棵每一个节点的键值都不小于（大于）其孩子（如果存在）的键值的树。大顶堆是一棵完全二叉树，同时也是一棵最大树。小顶堆是一棵完

　　全完全二叉树，同时也是一棵最小树。

　　需要注意的问题是：堆中的任一子树也还是堆，即大顶堆的子树也都是大顶堆，小顶堆同样。

　　

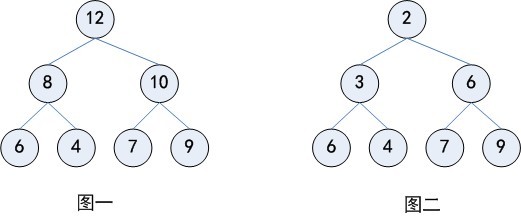
　　如图一为大顶堆，图二为小顶堆（摘自CSDN博客）

2.堆的一些基本性质：

　　　　（1）. 堆的插入和删除操作，运行时间为 O(logn)，n 为树上结点的个数

　　删除与插入同理，删除时需要注意的问题就是，删除一个元素之后，需要重新调整堆的结构，使其成为新的堆。

　　　　（2）.堆可以看成是一棵完全二叉树，除最后一层其余每层结点都是满的。

　　（非常重要！！）
　　（非常重要！！）
　　（非常重要！！）

　　重要的事情说三遍（讲究）；

3.代码的一些基本实现（最小堆的实现，最大堆和最小堆差不多）

　　不懂原理的可以看下这个：堆的原理

　　堆的基本操作：

　　　　上升；下沉；插入；弹出；

　　（1）上升

　　　　单一个很小点插入树的最后面，我们要将他移到前面，所以我们就要这个数和他父节点进行比较；

　　　　代码：

　　　　

void bup(int x)
{
    while(x!=1)
    {
        if(a[x>>1]>a[x])//如果它的值比它“父亲”大，就要进行交换（x>>1）
           //是x/2，我想大家都知道；
            swap(a[x>>1],a[x]);//交换
        else
            break;//如果不的话就可以结束了
        x>>=1;//将x缩小一倍，继续向上找；
    }
}

　　（2）下沉

　　　　单插入数很大时，就需要将将他下沉，此时就需要将他和他左子节点比较后，再和他右子点进行比较；

　　　　代码：

　　　　

void bdown(int x)
{
    int t;
    while((x<<1)<=cnt)
    {
        t=a[x]>a[(x<<1)]?(x<<1):x;//和他的左子节点进行比较如果大了就                        进行交换;
        if((x<<1)+1<=cnt)//再和他右子节点进行比较
            t=a[t]>a[(x<<1)+1]?(x<<1)+1:t;
        if(x==t)//如果相等就结束
            break;
        else
            swap(a[t],a[x]);
        x=t;
    }
}

　　（3）插入

　　　　插入是堆的特别多的操作，也很重要

　　　　代码：

　　　　

void bpush(int x)
{
    a[++cnt]=x;
    bup(cnt);
}

　　（4）弹出

　　　　弹出时你会发现一棵树变成两棵树，所以我们需要连起来；

　　　　代码：

　　　　

void bpop()
{
    a[1]=a[cnt--];//将第一位和最后一位交换
    bdown(1)；//将替换后第一位下沉；
}

　　　　近日就讲到这吧