点和直线的关系
一张参考图:
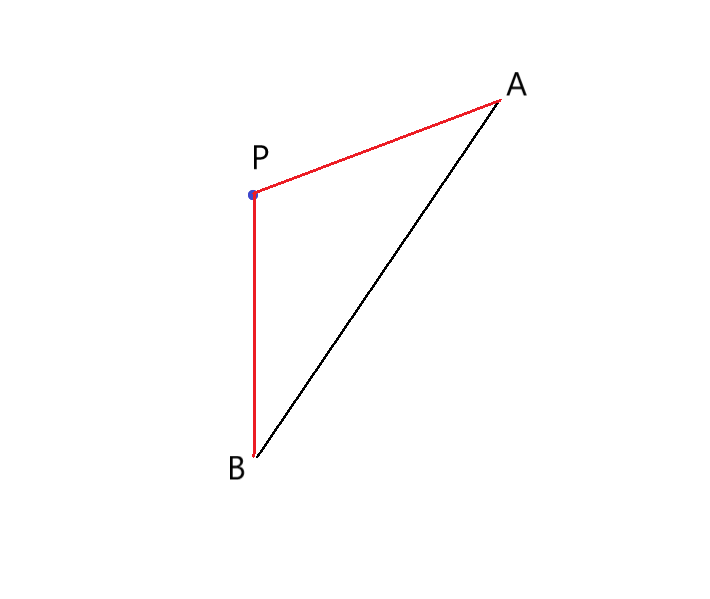
假设P为直线BA左侧一点,我们可以通过叉乘的方法来判断点在直线的哪一侧:如上图所示,PA × PB 的结果小于零,即叉乘的结果向量垂直纸面向里,则说明P点在直线AB的左侧,反之可以得出点在直线的右侧。注:此判定方法必须保证A在B上方。
知道判断方法后,下面要处理的就是如何计算两个向量的叉乘结果。 根据高中所学可得出:若两向量分别为( x1 , y1 ) 和 ( x2 , y2 ) 则其叉乘的向量模 = | x1 * y2 - x2 * y1 |。
具体代码实现为:

1 struct P //点集 2 { 3 int x, y; 4 P(){} 5 P(int xx,int yy) 6 { 7 x = xx; 8 y = yy; 9 } 10 P operator -(const P &b) const 11 { 12 return P(x - b.x, y - b.y); 13 } 14 int operator *(const P &b) const //点乘 15 { 16 return x * b.x + y * b.y; 17 } 18 int operator ^(const P &b) const //叉乘 19 { 20 return x * b.y - y * b.x; 21 } 22 }; 23 struct L 24 { 25 P x1, x2; //两点确定一条直线 26 L(){} 27 L(P xx1,P xx2) 28 { 29 x1 = xx1; 30 x2 = xx2; 31 } 32 } a[N]; 33 int sol(P x1,P x2,P x3) //判断 34 { 35 return (x2 - x1) ^ (x3 - x1); 36 }
还有一种理解方法为:
叉积的结果也是一个向量,是垂直于向量a,b所形成的平面,如果看成三维坐标的话是在 z 轴上,上面结果是它的模。
方向判定:右手定则,(右手半握,大拇指垂直向上,四指右向量a握向b,大拇指的方向就是叉积的方向)
若 a x b > 0表示a在b的顺时针方向上
若 a x b < 0表示a在b的逆时针方向上
若 a x b == 0表示a在b共线,但不确定方向是否相同
如果要判断一个点在线段的左边还是右边,只用计算一下这个点指向线段上面那个点的向量与这个点指向线段下面那个点的向量的叉积,如果是负这点就在线段的左边,如果是正就在右边。
其实叉乘还可以用来算三角形的面积(也是根据高中所学可得
