Bayan 2015 Contest Warm Up D题(GCD)

D. CGCDSSQ

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Given a sequence of integers a1, ..., an and q queries x1, ..., xq on it. For each query xi you have to count the number of pairs (l, r)such that 1 ≤ l ≤ r ≤ n and gcd(al, al + 1, ..., ar) = xi.

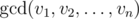 is a greatest common divisor of v1, v2, ..., vn, that is equal to a largest positive integer that divides all vi.

Input

The first line of the input contains integer n, (1 ≤ n ≤ 105), denoting the length of the sequence. The next line contains n space separated integers a1, ..., an, (1 ≤ ai ≤ 109).

The third line of the input contains integer q, (1 ≤ q ≤ 3 × 105), denoting the number of queries. Then follows q lines, each contain an integer xi, (1 ≤ xi ≤ 109).

Output

For each query print the result in a separate line.

Sample test(s)

input

3
2 6 3
5
1
2
3
4
6

output

1
2
2
0
1

input

7
10 20 3 15 1000 60 16
10
1
2
3
4
5
6
10
20
60
1000

output

14
0
2
2
2
0
2
2
1
1

题意：给出n个数，然后给q个询问，每次询问给出一个x。问有多少个区间的GCD是x

思路：比赛的时候yy的一个做法

            首先预处理出全部值的区间个数，这个用map存一下就好了，设为ans

            然后再开两个map 分别为mp mp2

            mp存的是以Xi结尾的全部区间的GCD的数的个数

            每次从Xi转移到Xi+1，仅仅须要累加以Xi结尾的区间的全部mp值与Xi+1的GCD的个数就好了，能够暂时赋给mp2，然后再赋给mp

            依照这种方法从左往右for一遍就好了

            然后查询的时候直接在ans里查就好了

            复杂度大概是O(N*(每一个数的因子个数))