跳台阶
题目描述
一只青蛙一次可以跳上1级台阶,也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
思路:典型的动态规划问题,动态规划问题最关键的是把事件中的各种情形抽象为状态,然后找到前后状态之间的关系,写出状态转化方程,再翻译为代码。
可以考虑到题目中跳到第n层台阶有多少种跳法为一个状态,设置一个辅助数组dp[n+1],dp[i]代表跳到第i层台阶的跳法总数。
因为一次只能跳1层或2层,那么dp[i]仅与dp[i-1]和dp[i-2]有关系。dp[i-1]可以通过跳一层得到dp[i],而dp[i-2]可以通过跳两层得到dp[i]。
所以状态转化方程为:
dp[i] = dp[i-1]+dp[i-2];
最后考虑边界条件:dp[1]= 1,dp[2] = 2;
1 public int JumpFloor(int target) { 2 if(target<=2) return target; 3 int[] dp = new int[target+1]; 4 dp[1] = 1; 5 dp[2] = 2; 6 for(int i=3;i<=target;i++){ 7 dp[i] = dp[i-1]+dp[i-2]*2; 8 } 9 return dp[target]; 10 }
跳台阶2
一只青蛙一次可以跳上1级台阶,也可以跳上2级……它也可以跳上n级。求该青蛙跳上一个n级的台阶总共有多少种跳法。
思路:此时条件变化为一次可以跳n步,则dp[i]与前面的状态都有关系。有了上面的基础,可以轻松写出状态转移方程为:
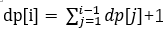
1 public int JumpFloorII(int target) { 2 if(target<=2) return target; 3 int[] dp = new int[target+1]; 4 dp[1] = 1; 5 dp[2] = 2; 6 7 for(int i=3;i<=target;i++){ 8 //因为可以一步跳到 9 dp[i] = 1; 10 for(int j=1;j<i;j++){ 11 dp[i] += dp[j]; 12 } 13 } 14 return dp[target]; 15 }