题目描述
如题,已知一个数列,你需要进行下面两种操作:
1.将某区间每一个数加上x
2.求出某区间每一个数的和
输入输出格式
输入格式:
第一行包含两个整数N、M,分别表示该数列数字的个数和操作的总个数。
第二行包含N个用空格分隔的整数,其中第i个数字表示数列第i项的初始值。
接下来M行每行包含3或4个整数,表示一个操作,具体如下:
操作1: 格式:1 x y k 含义:将区间[x,y]内每个数加上k
操作2: 格式:2 x y 含义:输出区间[x,y]内每个数的和
输出格式:
输出包含若干行整数,即为所有操作2的结果。
说明
时空限制:1000ms,128M
数据规模:
对于30%的数据:N<=8,M<=10
对于70%的数据:N<=1000,M<=10000
对于100%的数据:N<=100000,M<=100000
思路:
明显,这道题是一道线段树的模板题(虽然可以拿分块什么的水过去),在题解之前,先普及一些知识
什么是线段树?
我们知道,一般数据的储存是线性的,但这样对于区间问题并不优,下图所示的数列
我们如果想要
查询,那么时间复杂度为o(区间长度)有些别跟我说用前缀和的可以优化到O(1)级别,没用的,前缀和的修改时间复杂度更高
但修改呢??
如果你用正常修改,时间复杂度为O(区间长度),如果你要用前缀和,那么复杂度会为O(数列长度-区间左端);
显然,过于暴力,出题人想卡你的话你的时间复杂度会劣化到最大O(操作数*数列长度)
TLE 的飞起
那该怎么办呢?
大家学过堆吧?
一个O(nlogn^2)的暴力快排,上了二叉树就变成了O(nlogn)
快了好多啊!
那么我们这个操作能不能上树呢?
当然可以
线段树该出场了
看下面这幅图
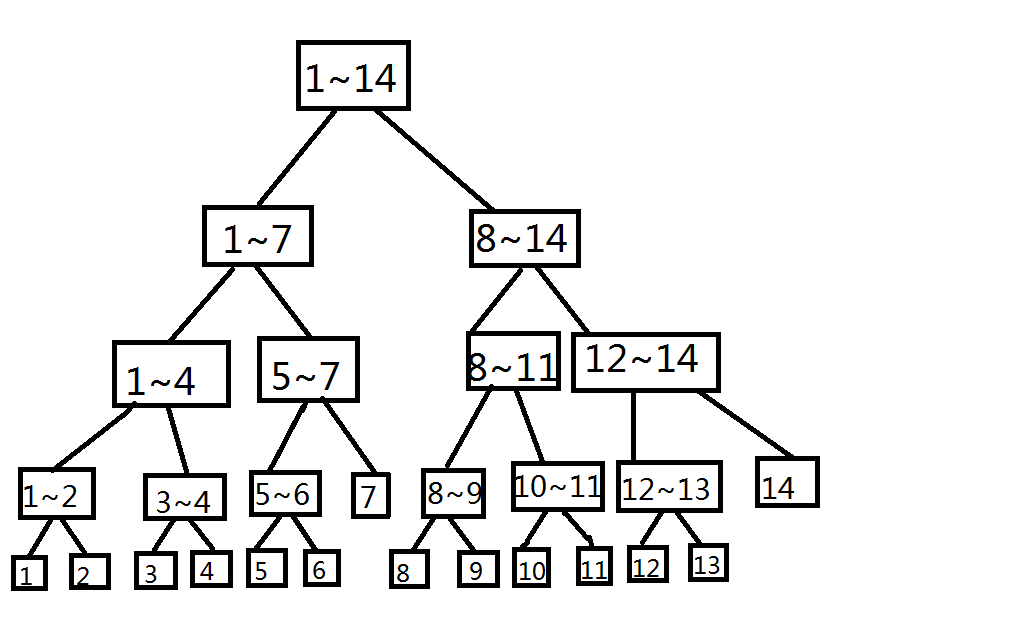
我们成功通过二分区间的方式建立了一棵树
此时查询,时间就省得多
比如说查询1~12,暴力的话复杂度为O(12),现在只要查询【1~7】,【8~11】,【12】三个区间即可
复杂度降到O(3log14);
别看就降了这么一点,如果n很大呢?
再说说插入
你们可能会说,插入以前是O(n),你这一来成了O(nlogn),还费劲了
谁说一定要插到底来着?我这么懒就不能插到中间吗?
答案是肯定的,lazy标记该出场了
比如说上图【4~11】每个加3
结果如下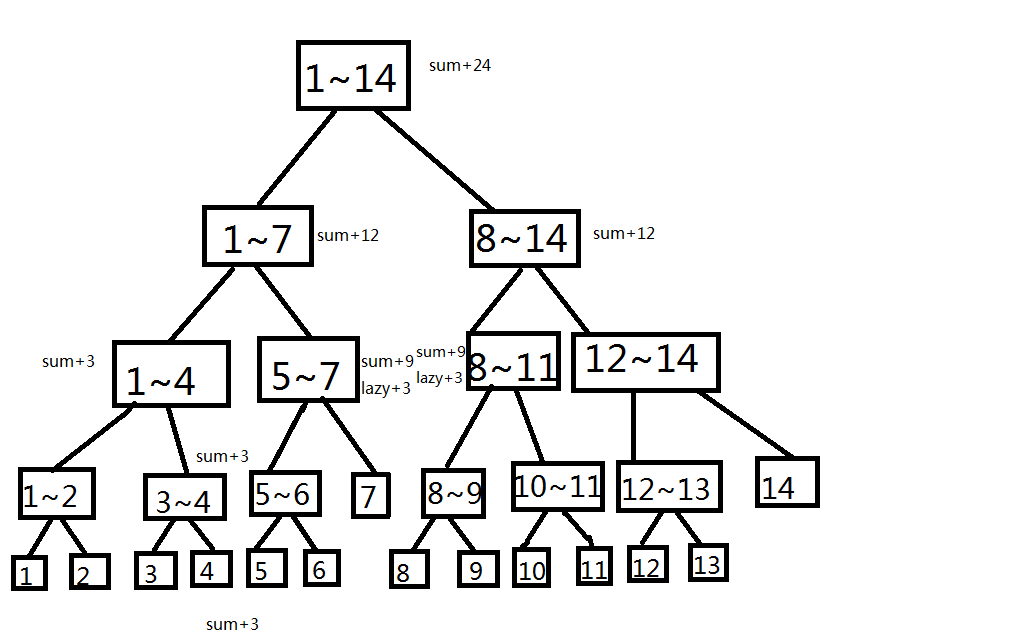
很显然,如果一个区间被要添加的区间完全包含,那你就不用再去下放到他的儿子,在他的位置上打个lazy标记jike
但同时你要注意细节,因为含有lazy标记的区间的子区间并没有被修改,所以在查询他的子区间时,lazy标记需要下放
同时如果你修改的只是一个元素,那也不需要lazy标记,直接改值即可
线段树的均摊复杂度为O(nlogn);
线段树的实现有两种方式,数组法和存边法,前者较为简单,但后者在写一些高阶线段树(比如说主席树)和平衡树时更优
我给出一组用数组解决的方法
见代码:
#include<iostream>
#include<cstdio>
using namespace std;
struct node{
long long lazy,sum;
}tree[400010];
int x[100010];
int n,m,a,b,c;
int as;
int sx,st,sk;
long long ans;
char pd;
void update(int l,int r,int i)//更新节点函数(就是下放函数)
{
if(!tree[i].lazy)
{
return;
}
int mid=(l+r)/2;
tree[i*2].sum+=tree[i].lazy*(mid-l+1);
tree[i*2+1].sum+=tree[i].lazy*(r-mid);
tree[i*2].lazy+=tree[i].lazy;
tree[i*2+1].lazy+=tree[i].lazy;
tree[i].lazy=0;
}
long long query(int tl,int tr,int l,int r,int i)//查询函数
{
if(tl>r||tr<l)
{
return 0;
}
if(tl<=l&&r<=tr)
{
return tree[i].sum;
}
update(l,r,i);
int mid=(l+r)/2;
return query(tl,tr,l,mid,i*2)+query(tl,tr,mid+1,r,i*2+1);
}
void add(int tl,int tr,int l,int r,int i,int val)//添加函数
{
if(tl>r||tr<l)
{
return;
}
if(tl<=l&&tr>=r)
{
tree[i].sum+=val*(r-l+1);
tree[i].lazy+=val;
return;
}
update(l,r,i);
int mid=(l+r)/2;
add(tl,tr,l,mid,i*2,val);
add(tl,tr,mid+1,r,i*2+1,val);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
}
void build(int l,int r,int i)//运用初始数据建树
{
if(l==r)
{
tree[i].sum=x[l];
return;
}
int mid=(l+r)/2;
build(l,mid,i*2);
build(mid+1,r,i*2+1);
tree[i].sum=tree[i*2].sum+tree[i*2+1].sum;
}
int main()
{
cin>>n>>m;
for(a=1;a<=n;a++)
{
cin>>x[a];
}
build(1,n,1);
scanf("
");
for(int i=1;i<=m;i++)
{
char ch;
int l,r,v;
scanf("%c",&ch);
if(ch=='2')
{
scanf("%d%d
",&l,&r);
ans=query(l,r,1,n,1);
printf("%lld
",ans);
}
else
{
scanf("%d%d%d
",&l,&r,&v);
add(l,r,1,n,1,v);
}
}
}