CodeForces 622D Optimal Number Permutation

是一个简单构造题。

请观察公式：

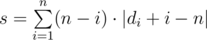
绝对值里面的就是 |di-(n-i)|，即di与（n-i）的差值的绝对值。

事实上，对于任何n，我们都可以构造出来每一个i的di与（n-i）的差值为0。

换句话说，就是这个最小值一定可以构造出来是0。

假设输入是6：
那么可以这样构造：1 3 5 5 3 1 2 4 6 4 2 6

假设输入是7：
那么可以这样构造：1 3 5 7 5 3 1 2 4 6 6 4 2 7

从上面就能看出怎么构造了，n最后放空缺的两个位置，剩下的从小到大一个一个放，奇数放左边构造，偶数放右边构造。

#include <stdio.h>
#include <algorithm>
#include <string.h>
#include <queue>
#include <stack>
#include <map>
#include <vector>
using namespace std;

const int maxn = 2*500000 + 10;
int n;
int ans[maxn];

int main()
{
    scanf("%d", &n);
    memset(ans, 0, sizeof ans);
    int left = 1, right = n + 1;
    for (int i = 1; i <= n - 1; i++)
    {
        if (i % 2 == 1)
        {
            ans[left] = i;
            ans[left + n - i] = i;
            left++;
        }
        else
        {
            ans[right] = i;
            ans[right + n - i] = i;
            right++;
        }
    }
    for (int i = 1; i <=2* n; i++) if (!ans[i]) ans[i] = n;
    for (int i = 1; i <= 2*n; i++) printf("%d ", ans[i]);
    printf("
");
    return 0;
}