机器学习算法之降维

　　在机器学习的过程中，我们经常会遇见过拟合的问题。而输入数据或features的维度过高就是导致过拟合的问题之一。。维度越高，你的数据在每个特征维度上的分布就越稀疏，这对机器学习算法基本都是灾难性的。所有出现了很多降维的方法。今天我们要讨论的就是LDA降维。

LDA降维的思路是：如果两类数据线性可分，即：存在一个超平面，将两类数据分开。则：存在模旋转向量，将两类数据投影到一维上，并且依然是线性可分的。

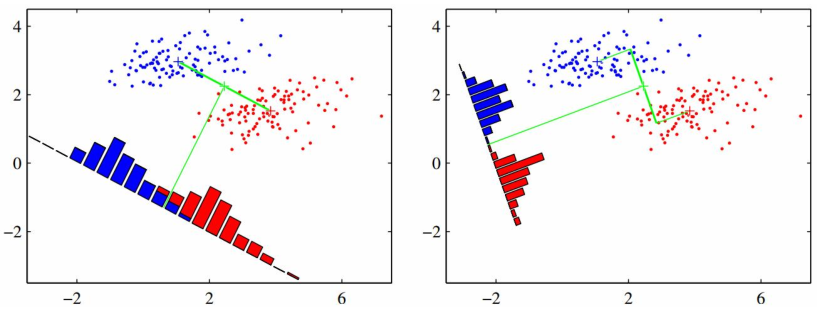
提出问题

假设未定一组N个带标记的数据（X_i，C_i），其中，标记C分两类，即：C_i =0 或C_i=1，设计分类器，将数据分开。如果x的维度很高，甚至比N还多，这时候就需要降维了。

解题过程

1、根据线性变换，将X降成一维的

假定旋转向量为W，将数据X投影到一维y，得到 y =W^TX ，其中输入数据X，旋转向量W。

如此就将原来我x维的向量转换为一维，利用分类算法将数据分类为C。从而，可以找到阈值W_0，如果y>W₀为一类，y<W₀为一类。

 2、计算每个分类的类内均值和方差

令C1类有N1个元素，C2有N2个元素，计算投影前的类内均值和投影后的类内均值和松散度（方差）：

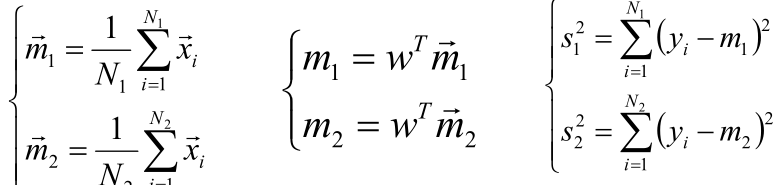
3、寻找Fisher判别准则

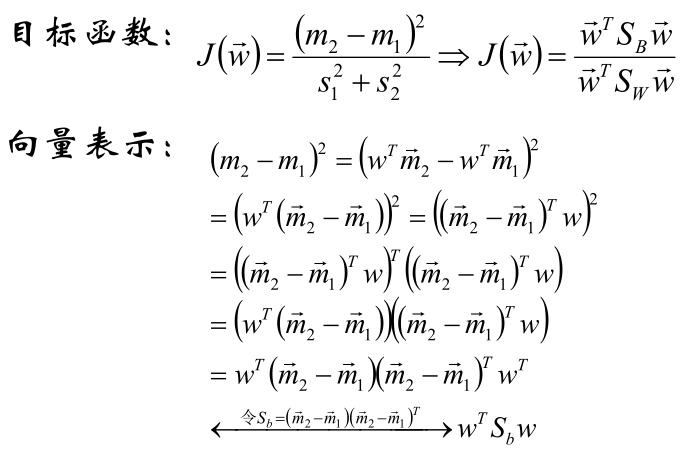
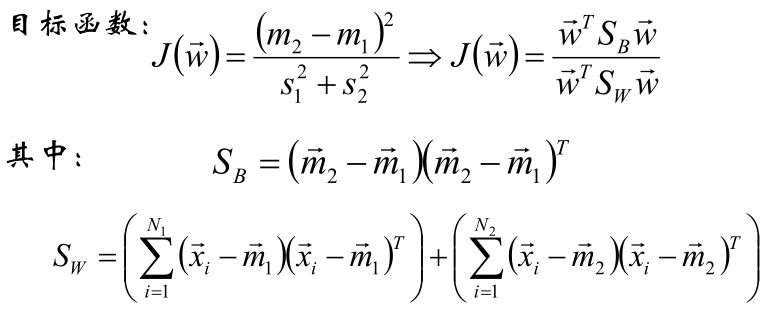
4、对目标函数进行优化

也就是对目标函数求导后取极值。

倒数为：

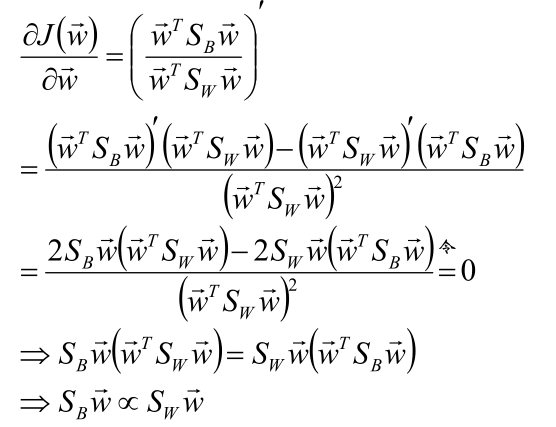
 推导得到， 三者同方向。

主题模型------主成分分析PCA

PCA和LDA的区别

LDA：分类性能最好的方向

PCA：样本点投影具有最大方差的方向

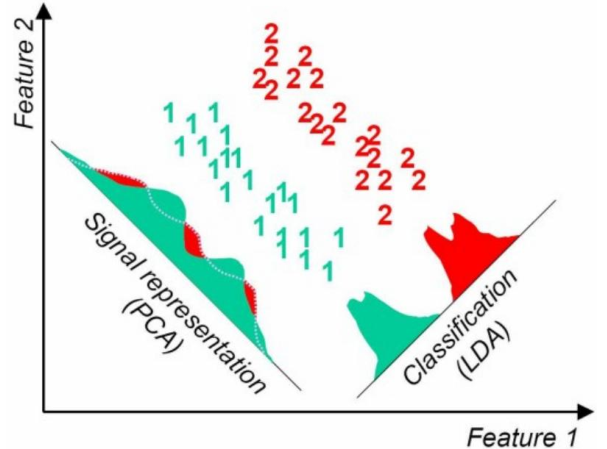
实际问题往往需要研究多个特征，而这些特征就有一定的相关性。

将多个特征综合为少数几个代表性特征。组合后的特征既能够代表原始特征的绝大部分信息，又互不相关，降低相关性。这种提取原始特征的主成分的方法就叫主成分分析。

问题的提出：

对于包含n个特征的m个样本的数据，将每个样本标记成行向量，得到了矩阵A：

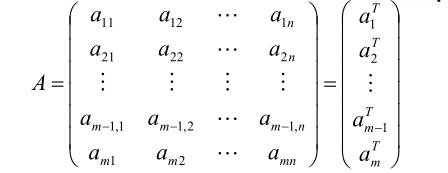
解题的思路：

寻找样本的主方向U：将m个样本的值投影到某直线L上，得到m个位于直线L上的点，计算m个投影点的方差。认为方差最大的直线方向为主方向。   

 假设样本去均值了

求方差，PCA的核心推导过程

取投影的直线L的延伸方向u，计算AXu的值

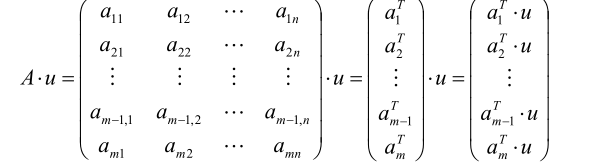
求向量A X u的方差

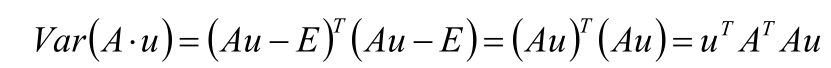
目标函数：J（u）= u^TA^TAu

目标函数求驻点：

由于u数乘得到的方向和u相同，因此，增加u是单位向量的约束，即：||u||₂=1 = u^Tu

 建立Lagrange的方程：

L（u）=  u^TA^TAu -λ （u^Tu-1）

求导：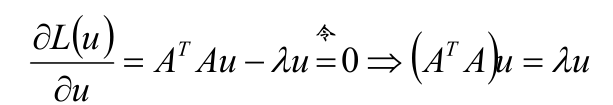

分析A^TAu = λu

若A中的样本都是去均值化的，则A^TA与A的协方差矩阵仅仅相差系数n-1

u是A^TA的特征向量，λ的值的大小为原始观测数据的特征向量在向量u的方向上投影值的方差

PCA的重要应用

去噪、降维 、模式识别、分析数据胡相关性以及多源融合等