动态规划作业-多段图的最短路径问题

多段图的最短路径问题

问题：设图G=（V,E）是一个带权有向图，如果把顶点集合V划分成k个互不相交的子集V_i（2<=k<=n,1<=i<=k）,

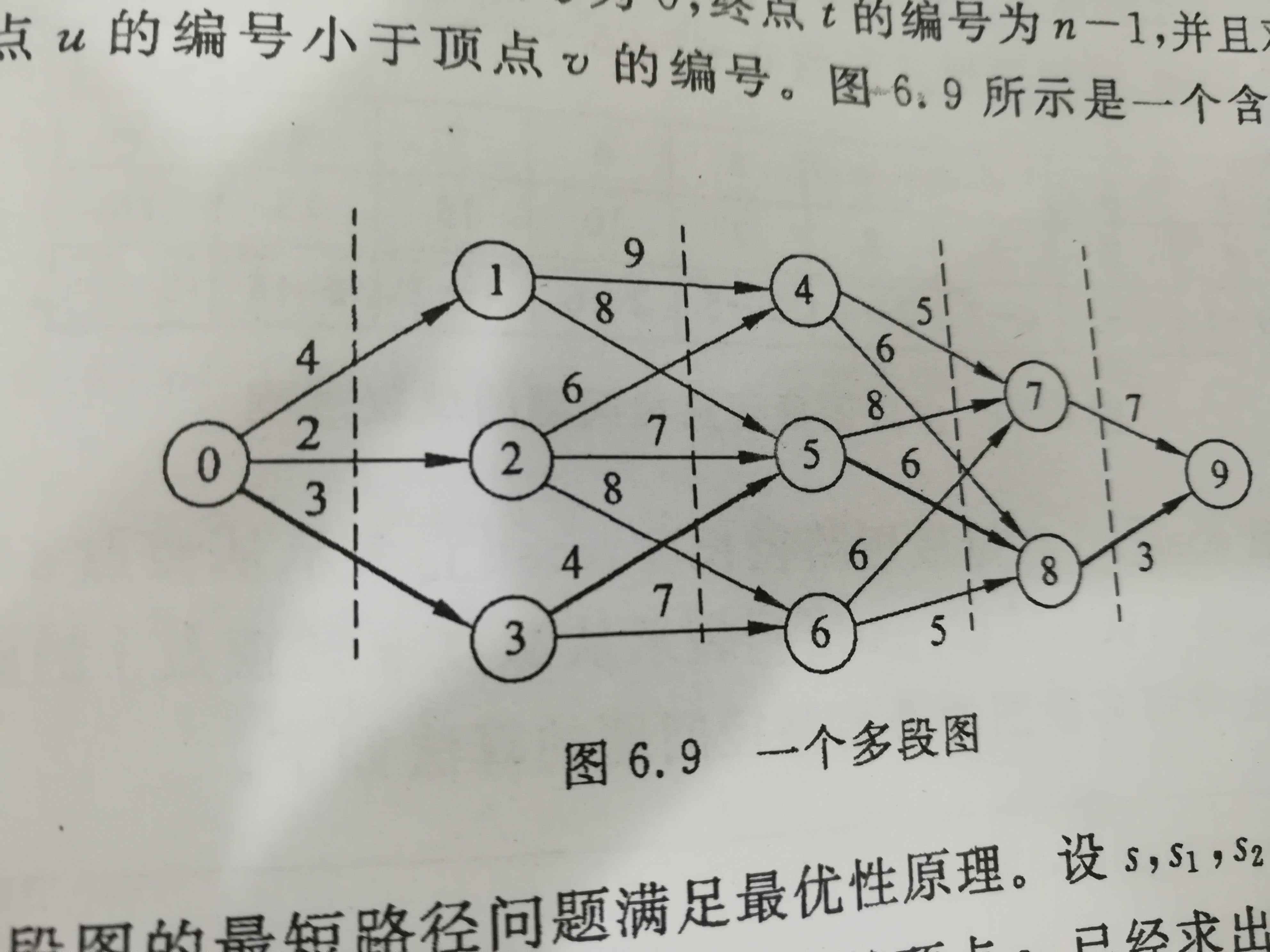
          使得E中的任何一条边<u,v>，必有u∈V_i, v∈V_i+m(1<=i<k,1<i+m<=k),则称图G为多段图，称s∈V₁为源点，

         t∈V_k为终点。

         多段图的最短路径问题为从源点到终点的最小代价路径。

子问题：设C_uv表示多段图的有向边<u,v>上的权值，将从源点s到终点t的最短路径长度即为d(s,t),

              考虑原问题的部分解d(s,v)，显然有下式成立

             d(s,v)=Csu                                  （<s,v>∈E）

             d(s,v)=min(d(s,u)+Cuv)            (<u,v>∈E)

算法：多段图的最短路径问题

输入：多段图的代价矩阵

输出：最短长度及路径c[n][n]

1.循环变量j从1~n-1重复下述操作，执行填表工作

   1.1考察顶点j的所有入边，对于边<i,j>∈E,执行下述操作

       1.1.1cost[j]=min{cost[i]+c[i][j]}；

       1.1.2path[j]=使cost[i]+c[i][j]最小的i;

     1.2 j++;

2.输出最短路径长度cost[n-1]；

3.循环变量i=path[n-1].循环直到path[i]=0,输出最短路径经过的顶点；

   3.1 输出path[i];

   3.2 i=path[i]

#include<iostream>
#include<algorithm>
#include<stdio.h>
#define Max 0xffff
using namespace std;
//动态规划求最短路径
void dp_path(int c[][100], int *cost, int *path) {
    int m, n;
    cout << "输入顶点个数和边个数" << endl;
    cin >> n >> m;
    //初始化代价矩阵
    for (int i = 0; i < n; i++)
        for (int j = 0; j < n; j++)
            c[i][j] = Max;
    //输入代价矩阵
    int u, v, s;
    for (int i = 0; i < m; i++) {
        cin >> u >> v >> s;
        //cout<<u<<v<<s<<endl;
        c[u][v] = s;
    }
    for(int i=0;i<n;i++)
        cost[i]=Max;
    path[0] = -1;
    cost[0] = 0;
    for (int j = 1; j < n; j++) {
        for (int i = j-1; i >=0; i--) {
            if (cost[j] > cost[i] + c[i][j]) {
                path[j] = i;
                cost[j] = cost[i] + c[i][j];
            }
        }
    }
    cout<<cost[n-1]<<endl;
    int i=path[n-1];
    cout<<path[n-1]<<endl;
    while(path[i]>=0){
        cout<<path[i]<<endl;
        i=path[i];
    }
}
int main()
{
    int c[100][100], cost[100], path[100];
    dp_path(c, cost, path);
    getchar();
    return 0;
}