Codeforces 1400E Clear the Multiset(贪心 + 分治)

链接：https://codeforces.com/problemset/problem/1400/E
来源：Codeforces

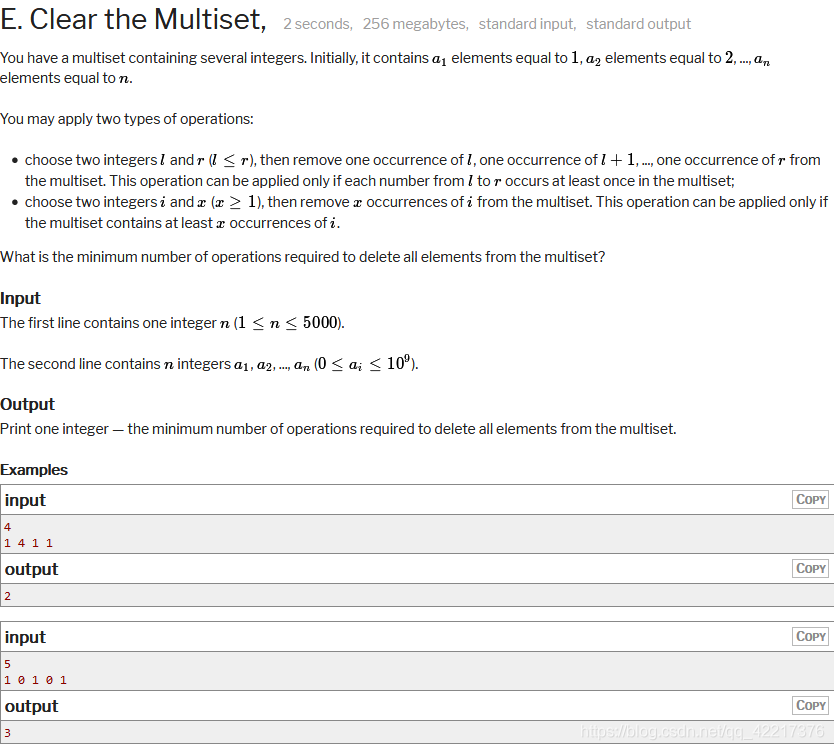
  思路：给你一个数组，现在你可以进行两种操作，操作1：将一段没有 0 的区间进行减一的操作，操作2：将 i 位置上的元素归零。最终问：将这个数组的全部元素归零后操作的最少的次数。首先如果我们只使用操作 2，那么一个区间内最多操作 (r - l + 1) 次。如果操作 1 和 操作 2 一起使用，我们可以贪心 + 分治的方式来求出操作次数，如果现在是一个区间，那么我们找到区间内最小的值 (cnt1)，此时我们进行操作操作 1 的次数就是 (cnt1)，当前这个位置的数字就归零了，此时这个数字左右两边还有可能进行重复的操作，那么当前操作的次数就是 cnt1 + 左右两边区间可以操作的次数，这个时候我们需要和只进行操作 2 进行比较，判断那种方式可以得到最小的操作次数。如果在递归的过程中最后只是剩下一个不为 0 的数字，那么我们进行一次操作 2。

#include<bits/stdc++.h>
using namespace std;

typedef long long ll;
const int maxn = 5e3 + 10;
int a[maxn];

int solve(int l, int r) {
	if(l > r) return 0;
	else if (l == r) {
		if(a[l] == 0) return 0;
		else return 1;
	} 
	int cnt1 = 1e9 + 10, mid;
	for(int i = l; i <= r; ++ i) {
		if(a[i] < cnt1) {
			cnt1 = a[i];
			mid = i;
		}	
	}
	for(int i = l; i <= r; ++ i) a[i] -= cnt1;
	return min(cnt1 + solve(l, mid - 1) + solve(mid + 1, r), r - l + 1);
}

int main() {
	int n; scanf("%d", &n);
	for(int i = 1; i <= n; ++ i) scanf("%d", &a[i]);
	int ans = solve(1, n);
	printf("%d
", ans);
	return 0;
}