P1886 滑动窗口

题目描述

现在有一堆数字共N个数字（N<=10^6），以及一个大小为k的窗口。现在这个从左边开始向右滑动，每次滑动一个单位，求出每次滑动后窗口中的最大值和最小值。

例如：

The array is [1 3 -1 -3 5 3 6 7], and k = 3.

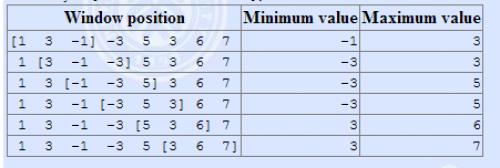
输入输出格式

输入格式：

输入一共有两行，第一行为n,k。

第二行为n个数(<INT_MAX).

输出格式：

输出共两行，第一行为每次窗口滑动的最小值

第二行为每次窗口滑动的最大值

输入输出样例

输入样例#1：

8 3
1 3 -1 -3 5 3 6 7

输出样例#1：

-1 -3 -3 -3 3 3
3 3 5 5 6 7

说明

50%的数据，n<=10^5

100%的数据，n<=10^6

感觉自己写代码越来越精简了。

stl里提供了一种叫做deque的双端队列。

这种队列支持在队首和队尾插入或者删除。

这样正好解决了queue不用应用于单调队列的缺陷。

关于deque的各种用法。

一张图足以概览

对于本题而言。查询最大最小值其实就是改一下入队条件的问题，

一个三目运算符解决

#include<iostream>
#include<cstdio>
#include<deque>
using namespace std;
const int MAXN=2000050;
const int maxn=0x7fffffff;
void read(int &n){char c='+';int x=0;bool flag=0;while(c<'0'||c>'9'){c=getchar();if(c=='-')flag=1;}
while(c>='0'&&c<='9'){x=x*10+(c-48);c=getchar();}flag==1?n=-x:n=x;}
int n,k;
int a[MAXN];
struct node
{
    int w,p;
    node (int a,int b)    {w=a;p=b;}
};
deque<node>q;
void find(bool how)
{
    while(q.size())     q.pop_front();
    for(int i=1;i<=n;i++)
    {
        while(q.size()!=0&&(how==0?(q.back().w<a[i]):(q.back().w>a[i])))    q.pop_back();
        q.push_back(node(a[i],i)); 
        while(q.front().p<=(i-k))    q.pop_front();
        if(i>=k)    printf("%d ",q.front().w);
    }
    printf("
");
}
int main()
{
    read(n);read(k);
    for(int i=1;i<=n;i++)    read(a[i]);
    find(1);find(0);
    return 0;
}